[科普中国]-功率有限信号-

定义

连续时间信号f（t）的能量E和功率P分别定义为：

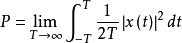
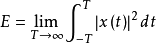
离散时间信号f（k）的能量E和功率P分别定义为：

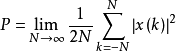
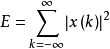
若信号能量有限，即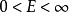 ,且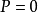，则称此信号为能量信号；若信号功率有限，即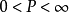，且E趋近于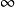，则称此信号为功率信号。

功率有限信号也就是平均功率大于零且有限的信号。1

特点功率有限信号的功率大于零且有限，能量无限。

一个信号不可能既是功率信号，又是能量信号，但可以既非功率信号，又非能量信号。一般地，周期信号和随机信号是功率有限信号2。

如何判断功率信号和能量信号呢？

信号的能量和功率是信号与系统分析里的基本概念或称通用概念，它的定义不会专门去考虑去照顾某一个特定信号的情况。通俗的说，时间不因你而存在，也不因你而消亡。过去、现在和将来，都是信号与系统这门学科需要关注的时间范围。为了广泛的适应性，这两个基本概念的积分时间都是无穷大。

根据两种信号的特点，在无限时间的周期信号为功率有限信号，而能量信号一定为非周期信号。非周期信号又分为三种。一是能量信号：持续时间有限的脉冲信号，且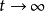时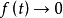，，一种是功率信号：持续时间无限，但幅度有限的信号；一种是既非功率又非能量信号，当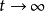时，。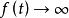

通信系统性能功率是能量传递的速率，它决定着发射机的电压和无线系统中必须考虑的电磁场强度（例如连接发射机和天线的波导中的电磁场，天线发射元件周围的电磁场）。例如在无线通讯系统中发射机的射频输出功率就很重要，发射功率越大，通信距离越大；从理论上说发射功率可无限制地增加，但实际上由于受成本或技规的限制，发射机的输出功率也是有限的。

信号的频率特性有四种：即功率信号的频谱、能量信号的频谱密度(简称频谱)、能量信号的能量谱密度、功率信号的功率谱密度。

能量信号的频谱密度S(f)和周期性功率信号的频谱Cn的主要区别有两点：

S(f)是连续谱，Cn是离散谱；
S(f)的单位是伏/赫，而Cn 的单位是伏。
能量信号的能量有限，并分布在连续频率轴上，所以在每个频率点f上信号的幅度是无穷小；只有在一小段频率间隔df上才有确定的非零振幅。功率信号的功率有限，但能量无限，它在无限多的离散频率点上才有确定的振幅。|S(f)|^2,成为能量谱密度，单位(J/Hz)，表示在频率f处宽度为df的频带内的信号能量，也可以看成是单位频带内的信号能量。
对于功率信号，由于具有无穷大能量，所以不能计算功率信号的能量谱密度，但可以求功率谱密度，将信号s(t)截断为长度等于T的一个截短信号，这个截短信号就成为一个能量信号了，对于这个能量信号，用傅立叶变换可求出其能量谱密度。于是，可以求出信号的功率谱密度。3