[科普中国]-中线定理

中线定理是一种数学原理，指的是三角形一条中线两侧所对的边平方和等于底边平方的一半与该边中线平方的两倍的和1。

定理简介中线定理（pappus定理），又称重心定理，是欧氏几何的定理，表述三角形三边和中线长度关系。2

定理内容：三角形一条中线两侧所对边平方的和等于底边的平方的一半加上这条中线的平方的2倍。

即，对任意三角形△ABC，设是I线段BC的中点，AI为中线，则有如下关系：

AB2+AC2=2BI2+2AI2

或作AB2+AC2=BC2+2AI2

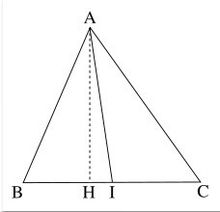
证明中线定理即为斯台沃特定理在中点时的结论，可由斯台沃特定理直接得出，但是斯台沃特定理不容易理解。下面有四种比较容易理解的方法。

第一种如图，在△ ABC中，AI为BC边上的中线。求证：AB2+AC2= (BC)2+2AI2

以BC的中点I为原点，直线BC为x轴，射线IC方向为x轴正方向，建立如图所示的平面直角坐标系。设A点坐标为（m，n），B点坐标为（-a，0），则C点坐标为（a，0）。

过A点做AD⊥x轴交x轴于点D，AE⊥y轴交y轴于点E，则D（m，0），E（0，n）。

由勾股定理可得

AO²=m²+n²,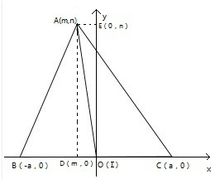

AB²=(a+m)²+n²=a²-2am+m²+n²,

AC²=(a-m)²+n²=a²+2am+m²+n².

∴AB²+AC²=a²+2am+m²+n²+a²-2am+m²+n²
=2a²+2m²+2n²=2a²+2(m²+n²)

又∵AO²=m²+n²,

∴AB²+AC²=2a²+2AO²

又∵B（-a，0），C（a，0）,

∴a=BC

∴a²=BC²

∴2a²=2·BC²=BC²

∴AB²+AC²=BC²+2AO²=BC²+2AI².

第二种如图，利用余弦定理来证明。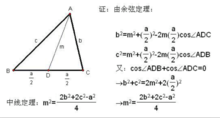

第三种如图，AI是△ABC的中线，AH是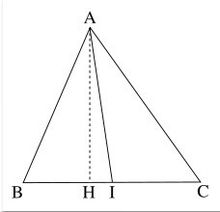高线。利用勾股定理来证明。3

在Rt△ABH中，有AB²=AH²+BH²

同理，有AI²=AH²+HI²，AC²=AH²+CH²

并且BI=CI

那么，AB²+AC²

=2AH²+BH²+CH²

=2(AI²-HI²)+(BI-IH)²+(CI+IH)²

=2AI²-2HI²+BI²+IH²-2BI×IH+CI²+IH²+2CI×IH

=2AI²+2BI²

第四种向量法证明中线定理。

如图，AI是△ABC的中线，分别取向量 、 、 、 、 。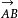

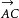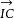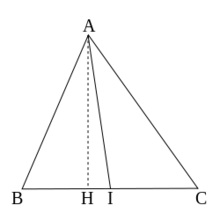
则

注意到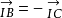 并且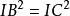

∴得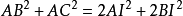

另一个结论在以上讨论中，通过两式相减，还可以得到**|AB^2-AC^2|=2BC*IH**。 （H为垂足）

本词条内容贡献者为:

郎奠波 - 副教授 - 黑龙江财经学院