[科普中国]-相轨迹

线性系统的相轨迹

设系统的微分方程如下：

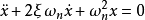
取相坐标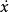 、 ，上述方程可化为

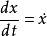
或

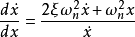
根据系统的不同特性，相轨迹主要有以下三种情况：1. 无阻尼 2. 欠阻尼 3. 过阻尼

无阻尼运动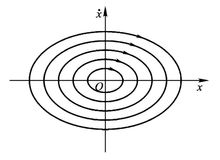无阻尼系统的 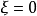，因此方程变为：

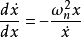
通过求解微分方程可以得到系统相轨迹方程为：

式中 为由初始条件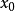 、 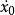决定的常数。

特性：

1. 相轨迹垂直穿过横轴

2. 在坐标原点处有唯一孤立奇点

欠阻尼运动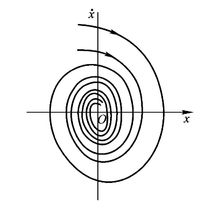对方程进行求解得到相轨迹：

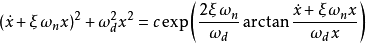
式中

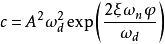
特性：

不管系统的初状态如何，经过一些衰减震荡，最后趋向于平衡状态。坐标原点是一个奇点，它附近的相轨迹是最终收敛于它的对数螺旋线（将相轨迹化为极坐标可看出），这种奇点称为稳定的焦点1。

过阻尼运动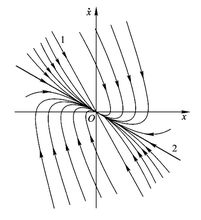通过求解微分方程可以得到相轨迹方程为：

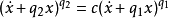
式中

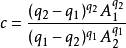
特性：

相轨迹为一簇抛物线，系统从任一初始状态出发，非周期的趋向于平衡状态。坐标原点为奇点，这种奇点称为稳定的节点1。

非线性系统的相轨迹继电型系统

继电型系统的非线性特性如上图所示。图(a)对应的数学表达式为

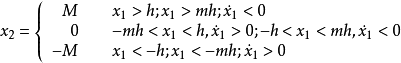
当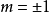 时可分别得到图(b)和图(c)

若系统的方框图如上所示，则图(b)系统的微分方程为 ，相轨迹如下图所示

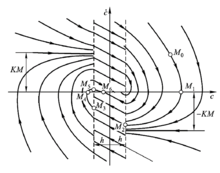
图(c)系统的微分方程为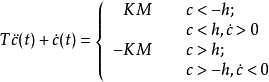 ，相轨迹如下图所示

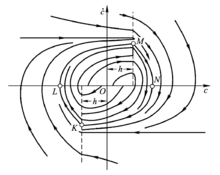
作图方法相轨迹的作图方法可分为：解析法和图解法，其中解析法主要针对可直接由方程求出 关系的、相对比较简单的系统，而图解法则针对不能直接由方程求出 关系的系统，原则上说，此法对任何非线性系统都适用，图解法根据具体的作图方法不同，可进一步分为等倾斜线法 , δ 法。下面介绍这三种方法。

解析法适用于简单的二阶线性系统或是分段线性系统（如继电型系统），可以通过微分方程求的相轨迹的表达式。但是一般来说求出微分方程的解析解是比较困难的，所以解析法具有较大的局限性，因此对于非线性系统常采用等倾斜线法来画相轨迹图像或者采用描述函数法进行近似分析。

等倾斜线法等倾斜线法适用于下述一般形式的系统1：

其基本思想是：考虑相轨迹通过相平面上的点，令 是常数，即相轨迹通过该点的斜率一定。分别取不同的斜率绘制曲线，这些线称为等倾斜线。在每条等倾线上画出表示斜率值的小线段，并进行光滑连接，就得到所求的相轨迹和相平面图。

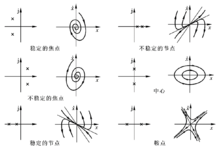
特征根和奇点对应关系二阶系统的特征根位置和奇点类型对应关系如下图所示