[科普中国]-多项式函数

一次函数概念

形如 y=kx+b （k为任意不为0的常数，b为任意常数）的函数叫做一次函数（linear function），也称线性函数，其图像在平面直角坐标系中可以用一条直线表示，当一次函数中的一个变量的值确定时，可以用一元一次方程确定另一个变量的值。

基本性质1.y的变化值与对应的x的变化值成正比例，比值为k

即：y=kx+b（k≠0) （k不等于0，且k，b为常数）

2.当x=0时，b为函数在y轴上的交点,坐标为(0,b).

当y=0时，该函数图象在x轴上的交点坐标为（-b/k，0）

3.k为一次函数y=kx+b的斜率,k=tanθ(角θ为一次函数图象与x轴正方向夹角,θ≠90°)

形、取、象、交、减。

4.当b=0时(即 y=kx)，一次函数图象变为正比例函数，正比例函数是特殊的一次函数.

5.函数图象性质：当k相同，且b不相等，图像平行；

当k不同，且b相等，图象相交于Y轴；

当k互为负倒数时，两直线垂直；

6.平移时：上加下减在末尾，左加右减在中间1。

二次函数概述一般地，形如y=ax^2+bx+c的函数叫做二次函数（quadratic function）。二次函数是自变量的最高次数为二次的多项式函数。其图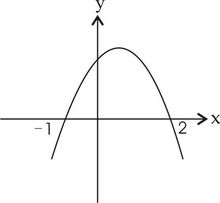像在平面直角坐标系中呈一条抛物线。

基本性质1、二次函数的图像是抛物线，但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图形。对称轴为直线x=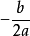 。对称轴与抛物线唯一的交点为抛物线的顶点P。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）。

2、抛物线有一个顶点P，坐标为P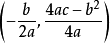 。当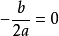 时，P在y轴上；当 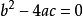时，P在x轴上。

3、二次项系数a决定抛物线的开口方向和大小。当a>0时，抛物线开口向上；当a0），对称轴在y轴左侧；当a与b异号时（即ab