[科普中国]-加速度

加速度（Acceleration）是速度变化量与发生这一变化所用时间的比值Δv/Δt，是描述物体速度变化快慢的物理量，通常用a表示，单位是m/s2。加速度是矢量，它的方向是物体速度变化（量）的方向，与合外力的方向相同。

定义加速度 (acceleration) 表征单位时间内速度改变程度的矢量。一般情况下，加速度是个瞬时概念，它的常用单位是米/秒²、米/秒²等。

在最简单的匀加速直线运动中，加速度的大小等于单位时间内速度的增量。若动点的速度v1经t秒后变成v2，则其加速度可表示为：

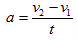
动点Q做一般空间运动时，速度矢量的变化和所经时间△t的比，称为△t时间内的平均加速度(图1)，记为a平：

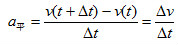
当时间间隔△t趋于零时，平均加速度的极限称为瞬时加速度(图1)，简称加速度，记为a：

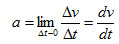
因而加速度的严格定义为：加速度矢量等于速度矢量对时向的导数，其方向沿着速端图的切线方向并指向轨迹的凹侧。关于加速度产生的原因，可参见牛顿运动定律。1

单位m/s2 或m·s-2（米每二次方秒）

加速度是矢量，既有大小又有方向。(方向由+、-号代表）

加速度的大小等于单位时间内速度的改变量；加速度的方向与速度变化量ΔV方向始终相同。特别，在直线运动中，如果加速度的方向与速度相同，速度增加；加速度的方向与速度相反，速度减小。

加速度等于对速度时间的一阶导数，等于位移对时间的二阶导数

物理意义表示质点速度变化的快慢的物理量。

举例：假如两辆汽车开始静止，均匀地加速后，达到10m/s的速度，A车花了10s，而B车只用了5s。它们的速度都从0变为10m/s，速度改变了10m/s。所以它们的速度变化量是一样的。但是很明显，B车变化得更快一些。我们用加速度来描述这个现象：B车的加速度（a=Δv/Δt，其中的Δv是速度变化量）>A车的加速度。

显然，当速度变化量一样的时候，花时间较少的B车，加速度更大。也就是说B车的启动性能相对A车好一些。因此，加速度是表示物体速度变化快慢的物理量。

注意1.当物体的加速度保持大小不变时，物体就做匀变速运动。如自由落体运动、平抛运动等。

当物体的加速度方向与大小在同一直线上时，物体就做匀变速直线运动。如竖直上抛运动。

2.加速度可由速度的变化和时间来计算，但决定加速度的因素是物体所受合力F和物体的质量M。

3.加速度与速度无必然联系，加速度很大时，速度可以很小；速度很大时，加速度也可以很小。例如：炮弹在发射的瞬间，速度为0，加速度非常大；以高速直线匀速行驶的赛车，速度很大，但是由于是匀速行驶，速度的变化量是零，因此它的加速度为零。

4.加速度为零时，物体静止或做匀速直线运动（相对于同一参考系）。任何复杂的运动都可以看作是无数的匀速直线运动和匀加速运动的合成。

5.加速度因参考系（参照物）选取的不同而不同，一般取地面为参考系。

6.当运动物体的速度方向与加速度（或合外力）方向之间的夹角小于90°时，速率将增大，速度的方向将改变；

当运动物体的速度方向与加速度（或合外力）方向之间的夹角大于90°而小于或等于180°时，速率将减小，方向将改变；

当运动物体的速度和方向与加速度（或合外力）方向之间的夹角等于90°时，速率将不变，方向改变。

7.力是物体产生加速度的原因，物体受到外力的作用就产生加速度，或者说力是物体速度变化的原因。说明当物体做加速运动（如自由落体运动）时，加速度为正值；当物体做减速运动（如竖直上抛运动）时，加速度为负值。

8.加速度的大小比较只比较其绝对值。物体加速度的大小跟作用力成正比,跟物体的质量成反比，加速度的方向跟作用力的方向相同，负号仅表示方向，不表示大小。

向心加速度

向心加速度（匀速圆周运动中的加速度）的计算公式：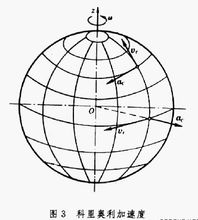

a=rω2=v2/r

说明：a就是向心加速度，推导过程并不简单，但可以说仍在高

中生理解范围内，这里略去了。r是圆周运动的半径，v是速度（特指线速度）。ω（就是欧姆的小写）是角速度。

这里有：v=ωr.

1．匀速圆周运动并不是真正的匀速运动，因为它的速度方向在不断的变化，所以说匀速圆周运动只是匀速率运动的一种。至于说为什么叫他匀速圆周运动呢？可能是大家说惯了不愿意换了吧。

2．匀速圆周运动的向心加速度总是指向圆心，即不改变速度的大小只是不断地改变着速度的方向。

3. 匀速圆周运动也不是匀变速运动，向心加速度的方向也在不断改变，但永远指向圆心且大小不变。

重力加速度

地球表面附近的物体因受重力产生的加速度叫做重力加速度，也叫自由落体加速度，用g表示。

重力加速度g的方向总是竖直向下的。在同一地区的同一高度，任何物体的重力加速度都是相同的。重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时，g变化不大。而离地面高度较大时，重力加速度g数值显著减小，此时不能认为g为常数

距离地面同一高度的重力加速度，也会随着纬度的升高而变大。由于重力是万有引力的一个分力，万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高，圆周运动轨道半径越小，需要的向心力也越小，重力将随之增大，重力加速度也变大。地球南北两极处的圆周运动轨道半径为0，需要的向心力也为0，重力等于万有引力，此时的重力加速度也达到最大。

由于g随纬度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665m/s2**;**作为重力加速度的标准值。在解决地球表面附近的问题中，通常将g作为常数，在一般计算中可以取g=9.80m/s2。理论分析及精确实验都表明，随纬度增大，重力加速度g的数值逐渐增大。如：

赤道g=9.780m/s2

广州g=9.788m/s2

武汉g=9.794m/s2

上海g=9.794m/s2

东京g=9.798m/s2

北京g=9.801m/s2

纽约g=9.803m/s2

莫斯科g=9.816m/s2

北极g=9.832m/s22

注：月球表面的重力加速度约为1.62 m/s2，约为地球表面重力加速度的六分之一。

自由落体中点速度：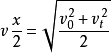

匀加速直线运动公式

1.匀加速直线运动的位移公式：

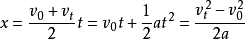
2.匀加速直线运动的速度公式:

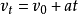
3.匀加速直线运动的平均速度(也是中间时刻的瞬时速度):

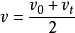
其中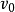 为初速度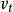， 为t时刻的速度，又称末速度。

4.匀加速度直线运动的几个重要推论:

(1)

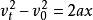
(以初速度方向为正方向，匀加速直线运动，a取正值； 匀减速直线运动，a取负值。)

(2) 时间中点的瞬时速度等于平均速度：

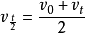
(3) AB段位移中点的即时速度：

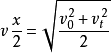
(4) 初速为零的匀加速直线运动,在前1s ,前2s,前3s……前ns内的位移之比为1^2:2^2:3^2……:n^2;

(5) 在第1s 内,第 2s内,第3s内……第ns内的位移之比为1:3:5……:(2n-1);

(6)在前1米内,前2米内,前3米内……前n米内的时间之比为1:2^(1/2):3^(1/2):……:n^(1/2)

(7) 初速无论是否为零,匀变速直线运动的质点,在连续相邻的相等的时间间隔内的位移之差相等，为一常数:△x= aT²(a一匀变速直线运动的加速度 T一每个时间间隔的时间)。

（8）竖直上抛运动: 上升过程是匀减速直线运动,下落过程是匀加速直线运动。全过程是初速度为VO,加速度为g的匀减速直线运动。

速度与加速度

物体运动时，如果加速度不为零，则处于变速状态。若加速度大于零，则为加速（即加速度和速度方向相同）；若加速度小于零，则为减速(即速度和加速度方向相反)。（提示：物理中的符号不同于数学中的符号，在数学中+、-号只代表是的标量，在物理中+、-号部分代表方向）

曲线加速运动

在加速度保持不变的时候，物体也有可能做曲线运动。比如，当你把一个物体沿水平方向用力抛出时，你会发现，这个物体离开桌面以后，在空中划过一条曲线，落在了地上。

物体在出手以后，受到的只有竖直向下的重力，因此加速度的方向和大小都不改变。但是物体由于惯性还在水平方向上以出手速度运动。这时，物体的速度方向与加速度方向就不在同一直线上了。物体就会往力的方向偏转，划过一条往地面方向偏转的曲线。

但是这个时候，由于重力大小不变，因此加速度大小也不变。物体仍然做的是匀加速运动，但不过是匀加速曲线运动。

量纲加速度可以有不同的单位，但其量纲是唯一的，即：L*T^(-2) 加速度也就是速度变化率

本词条内容贡献者为:

郎奠波 - 副教授 - 黑龙江财经学院