[科普中国]-重力加速度

重力加速度（Gravitational acceleration）是一个物体受重力作用的情况下所具 有的加速度。也叫自由落体加速度，用g表示。方向竖直向下，其大小由多种方法可测定。

通常指地面附近物体受地球引力作用在真空中下落的加速度，记为g。为了便于计算，其近似标准值通常取为980厘米/秒的二次方或9.8米/秒的二次方。在月球、其他行星或星体表面附近物体的下落加速度，则分别称月球重力加速度、某行星或星体重力加速度。

基础知识定义1重力加速度（Gravitational acceleration）是一个物体受重力作用的情况下所具有的加速度。 假设一个质量为m的质点与一质量为M的均匀球体的球心距离为r时，质量所受的重力大小约等于两物体间的万有引力，为：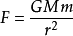

其中G为引力常数。 根据牛顿第二定律

F=ma=mg

可得重力加速度

三要素大小：与位置有关；（G=mg) （其中g=9.80665 m/s^2，为标准重力加速度）

方向：竖直向下；

作用点：重心1

证明自由落体运动时，a=g2。

证明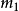： （ 为惯性质量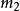， 为引力质量，经力学单位制统一后，两者数值上相等）

因为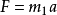

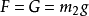
所以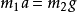

所以a=g2

自由落体⒈初速度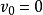

⒉末速度V=gt

⒊下落高度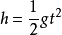 （从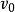 位置向下计算）

⒋推论**:**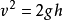

注：⑴自由落体运动是初速度为零加速度为g的匀加速直线运动，遵循匀变速直线运动规律；

⑵a=g=9.8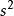m/ ≈10m/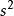 （重力加速度在赤道附近较小，在高山处比平地小，方向竖直向下）。

竖直上抛运动⒈位移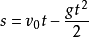

⒉末速度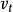 =v0-gt （g=9.8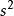m/ ≈10m/ ）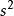

⒊有用推论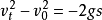

⒋上升最大高度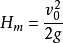 （抛出点算起）

⒌往返时间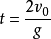 （从抛出落回原位置的时间）

注：⑴全过程处理：是匀减速直线运动，以向上为正方向，加速度取负值；

⑵分段处理：向上为匀减速直线运动，向下为自由落体运动，具有对称性；

⑶上升与下落过程具有对称性，如在同点速度等值反向等。△s=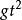

性质重力加速度g的方向总是竖直向下的。在同一地区的同一高度，任何物体的重力加速度都是相同的。重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时，g变化不大。而离地面高度较大时，重力加速度g数值显著减小，此时不能认为g为常数。

距离地面同一高度的重力加速度，也会随着纬度的升高而变大。由于重力是万有引力的一个分力，万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高，圆周运动轨道半径越小，需要的向心力也越小，重力将随之增大，重力加速度也变大。地理南北两极处的圆周运动轨道半径为0，需要的向心力也为0，重力等于万有引力，此时的重力加速度也达到最大。

通常指地面附近物体受地球引力作用在真空中下落的加速度，记为g。为了便于计算，其近似标准值通常取为980厘米/秒^2或9.8米/秒^2。在月球、其他行星或星体表面附近物体的下落加速度，则分别称月球重力加速度、某行星或星体重力加速度。

在近代一些科学技术问题中，需考虑地球自转的影响。更精确地说，物体的下落加速度g是由地心引力F（见万有引力）和地球自转引起的离心力Q（见相对运动）的合力W产生的（图1）。Q的大小为mω(RE+H）cosδ,m为物体的质量；ω为地球自转的角速度；RE为地球半径；H为物体离地面的高度；δ为物体所在的地球纬度。这个合力即实际见到的重力G=mg。地球重力加速度是垂直于大地水准面的。在海平面上g随纬度δ变化的公式（1967年国际重力公式）为：

g=978.03185（1+0.005278895*sinδ^2+0.00023462*sinδ^4）厘米/秒。

在高度为H的重力加速度g（1930年国际重力公式）同H和δ有关，即

g =978.049（1+0.005288*sinδ^2-0.000006*sin2δ^2)- 0.03086*H 厘米/秒，

式中H为以千米为单位的数值。

最早测定重力加速度的是伽利略。约在1590年，他利用斜面将g的测定改为测定微小加速度a=gsinθ，θ是斜面的倾角。测量重力加速度的另一方式是阿脱伍德机。1784年，G.阿脱伍德将质量同为Μ的重块用绳连接后，放在光滑的轻质滑车上，再在一个重块上附加一重量小得多的重块m（图2）。这时，重力拖动大质量物块，使其产生一微小加速度，测得a后，即可算出g。后人又用摆和2Μ+m各种优良的重力加速度计测定g。

地球上几个不同纬度处的g值见下表；从中可以看出g值随纬度的变化情况：

由于地球有自转，所以略微呈椭球形，在一般情况下，重力加速度的方向不通过地心。重力加速度的测定，对物理学、地球物理学、重力探矿、空间科学等都具有重要意义3

概念延伸地球表面在地球表面附近，一质点的自由落体加速度g与它的重力加速度a稍微不同，一个质点的重量mg与它所受的重力（万有引力和惯性力的共同作用叫重力）也不同，原因是地球会自转。若考虑地球自转，则：

(测量到的重量mg)=(万有引力)-(质量m×向心加速度(w^2)*R)

可以得到：

(自由落体加速度g)=(万有引力)-(向心加速度(w^2)*R)4

注意以上式子中的减法为矢量相减。自由落体加速度实际上是小于重力加速度的，方向也略有区别，在赤道上则相差最多，但由于地球的半径与自转周期的关系，两者大约只相差0.034m(s^2)，因此在日常使用的计算上，重量与重力之间的差异通常是可忽略的。

地表附近的所有物体下降的加速度都介于9.78和9.83m/(s^2);之间，差别是取决于纬度等因素(赤道最少，南北极最大)，标准重力加速度是9.80665 m/s^2;（为方便计算，一般使用9.81 m/(s^2);9.8 m/(s^2);或10 m(s^2);）。5

常用数值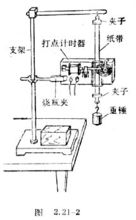由于g随经度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米/秒^2**;**作为重力加速度的标准值。在解决地球表面附近的问题中，通常将g作为常数，在一般计算中可以取g=9.80米/秒^2；。理论分析及精确实验都表明，随纬度的提高，重力加速度g的数值略有增大，如赤道附近g=9.780米/秒^2，

广州g=9.788米/秒^2。

武汉g=9.794米/秒^2。

上海g=9.794米/秒^2。

东京g=9.798米/秒^2。

北京g=9.801米/秒^2。

纽约g=9.803米/秒^2。

莫斯科g=9.816米/秒^2。

北极地区g=9.832米/秒^2。6

各纬度海平面的重力加速度（m/s^2）

|| ||

不同高度的重力加速度 (m/s^2）

|| ||

注：如果上升高度不大,则每升1km，g 减少0.03%。

重力加速度g不同单位制之间的换算关系为：重力加速度g = 9.81m/s^2**;= 981cm/s^2; = 32.18ft/s^2;**

注：图为测量的一种重力加速度试验单

月球表面的重力加速度约为1.62 m/s^2**;**，约为地球重力的六分之一

△g纬=8.14sin2φ×D（φ为纬度值，D为纬向距离、在北半球向北为正），即在北纬45°附近向北一公里 g增大8.14g.u.=8.14×10^-6m/s^2

△g高=-3.086△h（g.u.），即高度差距不太大时，每升高1米g减小3.086g.u.=3.086×10^-6m/s^2

精确计算严格说来，质点受到万有引力是质点的重力和质点随地球绕自转轴作匀速圆周运动产生向心力的矢量和。那么，重力就是质点受到万有引力和质点随地球绕自转轴作匀速圆周运动产生向心力的矢量差。

假设地球质量是M，质点质量是m，质点所在纬度是θ，海拔高度h，此处的地球半径是R，地球自转的角速度是ω，万有引力常数是G，质点和地球自转轴之间的距离是r，那么显然有r=(R+h)cosθ。此时，万有引力F引=GMm/(R+h)^2，向心力F向=mrω^2=mω^2(R+h)cosθ

由余弦定理得G^2=F引^2+F向^2-2F引F向cosθ

具体公式见图片。

上式是理论上的公式，实际应用可用下式

g=9.78049（1 + 0.0052884 (Sinθ）^2 - 0.0000059 *(Sin2θ） ^ 2） - 0.00000286h

计算方法因为F=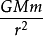 ,F=G=mg

所以g=GM/r^2（gr^2=GM被称为黄金代换）

G：引力常量=6.67259*10^-11N㎡/kg^2(m^3/k·gs^2）

M：中心天体质量/千克

r：天体中心与物体中心的距离/m

g的单位是m/s^2或N/kg

精确的重力加速度在近代一些科学技术问题中，需考虑地球自转的影响。更精确地说，物体的下落加速度g是由地心引力F（见万有引力）和地球自转引起的离心力Q（见相对运动）的合力W产生的（图1）。Q的大小为

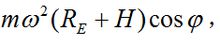
m为物体的质量；ω为地球自转的角速度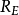； 为地球半径；H为物体离地面的高度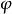； 为物体所在的地球纬度。这个合力即实际见到的重力W=mg。地球重力加速度是垂直于大地水准面的。在海平面上g随纬度 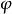变化的公式（1967年国际重力公式）为：

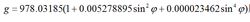
在高度为H的重力加速度g（1930年国际重力公式）同H和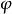 有关，即

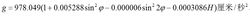
式中H为以米为单位的数值。

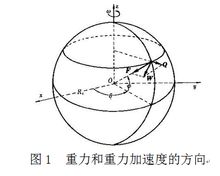
最早测定重力加速度的是伽利略。约在1590年，他利用斜面将g的测定改为测定微小加速度a=gsinθ，θ是斜面的倾角。测量重力加速度的另一方式是阿脱伍德机。1784年，G. 阿脱伍德将质量同为M的重块用绳连接后，放在光滑的轻质滑车上，再在一个重块上附加一重量小得多的重块m（图2）。这时，重力拖动大质量物块，使其产生一微小加速度，测得a后，即可算出g。后人又用摆和各种优良的重力加速度计测定g。

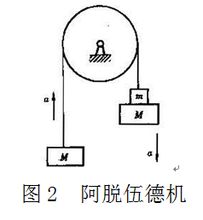
地球上几个不同纬度处的g值见下表；从中可以看出g值随纬度的变化情况：

由于地球是微椭球形的，加之有自转，在一般情况下，重力加速度的方向不通过地心，重力加速度的测定，对物理学、地球物理学、重力探矿、空间科学等都具有重要意义。

逃逸速度一个质量为m的物体具有速度v，则它具有的动能为mv^2/2。假设无穷远地方的引力势能为零（应为物体距离地球无穷远时，物体受到的引力势能为零，所以这个假设是合理的），则距离地球距离为r的物体的势能为-mar(a为该点物体的重力加速度，负号表示物体的势能比无穷远点的势能小）。又因为地球对物体的引力可视为物体的重量，所以有

GmM/r^2=ma

即a=(GM)/r^2.

所以物体的势能又可写为-GmM/r，其中M为地球质量。设物体在地面的速度为V，地球半径为R，则根据能量守恒定律可知，在地球表面物体动能与势能之和等于在r处的动能与势能之和，即

mV^2/2+(-GMm/R)=mv^2/2+(-GmM/r）。

当物体摆脱地球引力时，r可看作无穷大，引力势能为零，则上式变为

mV^2/2-GmM/R=mv^2/2.

显然，当v等于零时，所需的脱离速度V最小，即

V=2GM/R开根号，

又因为

GMm/R^2=mg,

所以

V=2gR开根号，

另外，由上式可见逃逸速度（第二宇宙速度）恰好等于第一宇宙速度的根号2倍。

其中g为地球表面的重力加速度，其值为9.8牛顿/千克。地球半径R约为6370千米，从而最终得到地球的脱离速度为11.17千米/秒。

不同天体有不同的逃逸速度，脱离速度公式也同样适用于其他天体。

天体计算宇宙总是那么奥妙无穷，我们知道天体的质量非常大，人们又是如何测量出天体的质量的呢？

一、 用万有引力定律和牛顿运动定律估算天体质量

在天体运动中，近似认为天体的运动是匀速圆周运动，在其运动过程中起决定因素的是万有引力，即万有引力提供天体做匀速圆周运动所需的向心力，有G(mM/r2）=m × （2π/T)2×r 其中周期可通过天文观测方式获得，从而可得天体质量为：M = [（2π/T)2×r3] / G

二 . 用万有引力计算天体轨道.

在天文尺度下物体的运动服从经典理论，因此可以从已知的边界条件（速度，位置，自旋）然后通过经典力学公式推算天体轨道，一个著名的例子是太阳系行星海王星的预测.（详见百度百科词条：海王星）

参考文献2

1、词条作者：高为炳．《中国大百科全书》74卷（第一版）力学 词条：重力加速度：中国大百科全书出版社，1987 ：596-597页．

本词条内容贡献者为:

郎奠波 - 副教授 - 黑龙江财经学院