测量不确定度是指测量结果含有的一个参数,用以“表征合理地赋予被测量之值的分散性”1。
来源实际工作中不确定度的来源一般有以下几点1:
被测量定义不完善
测量样本不能完全代表定义的被测量
被测量定义实现不理想
测量人员
环境
参数不准
测量仪器
测量方法和程序的近似和假设
在相同的测量下,重复测量中的随机变化
测量列中的粗大误差因不明显而未被剔除
A类评定贝塞尔法对于某量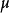 进行多次独立测量,得到测量列的分分布满足正态分布
进行多次独立测量,得到测量列的分分布满足正态分布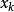 ~
~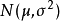 ,则单次测量的标准差估计为
,则单次测量的标准差估计为
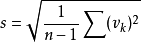
式中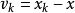 ,
,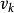 称为残差。该式称为贝塞尔公式,由贝塞尔在研究仪器误差理论时得到1。
称为残差。该式称为贝塞尔公式,由贝塞尔在研究仪器误差理论时得到1。
设测量测服从正态分布,则由最大残差得到标准差的估计为
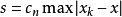
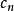 的取值见下表,该方法由中国计量科学研究院刘志敏研究员于1979年提出1。
的取值见下表,该方法由中国计量科学研究院刘志敏研究员于1979年提出1。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 |
| cn | - | 1.77 | 1.02 | 0.83 | 0.74 | 0.68 | 0.64 | 0.61 | 0.59 | 0.57 | 0.51 | 0.48 |
俄罗斯天文学家彼得斯采用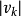 计算
计算 减弱了粗大误差值的影响1。
减弱了粗大误差值的影响1。
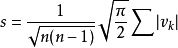
其他方法还有极差法、最大误差法等1
B类评定B类评定方法有别于统计分析法,是基于其他方法估计概率分布或假设服从某种分布评定标准不确定度的。关于B类评定主要是通过一定的实验,对测量列进行统计分析,以标准差表征其量值,其可靠性不仅与重复测量的次数有关,还与概率分布的类型有关。合理使用B类不确定度要求对经验及相关知识有透彻的了解,一般靠长期的实验经验逐步累积1。
倍数法如x取自制造说明书、校准证书、手册或其他来源,且给出的不确定度U(x)为标准差的k倍,则标准不确定度1:
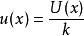
当估计值x受到多个独立因素的影响且影响的大小相近,可假设其服从正态分布1
1)若给出的不确定度U(x)对应的置信水准为90%、95%、99%、99.97%,可将不确定度除以适当的因子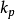 (
(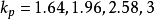 ),即可得到标准不确定度
),即可得到标准不确定度
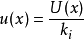
2)当x落入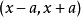 内的概率为50%,可取
内的概率为50%,可取
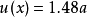
3)当 在
在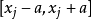 的概率为0.68,则
的概率为0.68,则
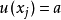
当X在[x-a,x+a]内各处出现的机会相等而区间外不出现时,X服从均匀分布,其最佳值x的标准不确定度为1:
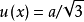
当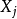 受到均匀分布的正余弦函数影响,它服从
受到均匀分布的正余弦函数影响,它服从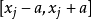 的反正弦分布,则最佳值
的反正弦分布,则最佳值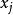 的标准不确定度1:
的标准不确定度1:
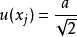
其他方法还有梯形分布与三角分布法、投影分布法等1
测量不确定度的合成合成标准不确定度的计算公式当测量结果受各种因素的影响而具有若干个不确定度分量时,测量结果的标准不确定度可用各标准不确定度的分量通过合成得到,一般用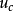 表示:
表示:

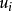 为第i个标准不确定度分量;
为第i个标准不确定度分量;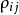 为第i个和第j个标准不确定度分量之间的相关系数;m为不确定度分量的个数1。
为第i个和第j个标准不确定度分量之间的相关系数;m为不确定度分量的个数1。
在间接测量中,被测量Y的估计值y是由N个其他直接测量的测得值的函数求得的,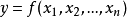 。若已知各直接测得值x的测量标准不确定度为
。若已知各直接测得值x的测量标准不确定度为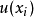 ,它对被测量估计值影响的传递函数为
,它对被测量估计值影响的传递函数为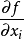 ,则由x_i引起被测量y的标准不确定度分量为1:
,则由x_i引起被测量y的标准不确定度分量为1:
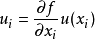
测量结果y的不确定度的计算公式为:
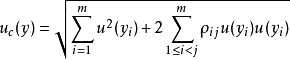
当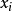 和
和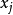 相互独立独立时,即
相互独立独立时,即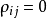 ,合成公式可以简化为:
,合成公式可以简化为:
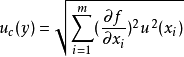




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国