定时抖动的积累是多中继数字传输系统中极为重要的问题。再生中继器的定时信号,通常采用直接从信号码流中提取的自定时方式。实际中,由于定时电路的不完善,传输中信号受噪声的干扰,接收端提取出来的定时信号呈现随时间不规则的晃动,即定时抖动。定时抖动使再生判决瞬间发生偏差,这不但使判决瞬间的信噪比恶化,而且还会反映到再生后的信号中,使再生后的信号产生相位调制,传到下一个中继器,形成抖动积累(jitter accumulation)。
关于电缆传输的抖动性能研究已比较完善。抖动分为与信号随机性有关的图案噪声和与信号无关的热噪声。但是,在光纤通信中,除了以上两个抖动源外,还存在第三个抖动源--散弹噪声。散弹噪声的统计特性与前两种噪声完成不同,且当采用雪崩光电二极管(APD)作光电检测器时,它是起主要作用约噪声源。
电缆中传输信号通常采用正负交替的脉冲序列,其频谱中没有1/T处的谱线,必须将信号进行非线性处理,才能定时提取。在光纤通信中,则常采用单极性归零码,这时的信号序列含有传输速率1/T处的谱线,故可直接提取定时信号,而不需要作预处理。通常把没有预处理的定时电路称作简单定时电路。文献利用定时抖动功率谱密度的统一范式,详细分析i割辰槽路(RC)式定时电路的抖动功率谱密度分布及抖动积累特性,给出抖动积累方差的简化公式。这些简化公式在工程估算中是十分方便的1。
抖动源随机性抖动源各种噪声源:在光缆系统中,除了一般电缆系统所具有的热噪声外,接收机的雪崩二极管还会产生可观的雪崩噪声。激光器本身会产生量子噪声、纽结噪声、模分配噪声及反射噪声。激光器与很短的光纤段相结合还会产生模式噪声。这些噪声的机理不尽相同,但其结果都会使信号脉冲波形发生随机畸变,从而使定时滤波器的输出信号波形产生随机的相位寄生调制,形成抖动。
激光器的跳模和光反馈:由于温度和其他条件的影响,激光器的工作模式会发生随机跳动,使传输信号的延迟发生变化,导致定时判决点偏离最佳时刻,形成抖动。这种激光器的跳模现象,如果与光源侧的不完善接头所造成的光反馈相结合,甚至会造成定时信息的暂时消失。但是,这种随机跳模所造成的影响是暂时的,不会形成恒定的损伤,而且在系统设计中可以设法尽量避免。
③定时滤波器失谐:定时滤波器的有效品质因数总是有限的,因而传输信息中靠近时钟频率的一小段连续谱也会得到输出。当滤波器失谐时,将产生不对称的输出波形,等效于非对称边带的调制,造成时钟分量幅度和相位上的调制。其中相位调制将弓!起定时抖动。
完全不相关的码型抖动:在码型相关抖动中有一部分是完全不相关的抖动,其积累特性如同随机噪声一样,可以按随机性抖动处理。
系统性抖动源在一个理想中继器中,信号码型对输出定时信号的相位没有影响。但是,实际的中继器总会有各种缺陷存在,这就会造成定时信号的相位变化,形成抖动。
码间干扰:目前的光纤制造技术还不能精确地控制光纤的色散特性,而均衡器又不希望做得很复杂,因而少量的码间干扰是容许的。随着温度变化和元器件老化,码间干扰会增大,使传输信号通过非线性元件后引起输出脉冲峰值位置的随机偏移,一`形成定时抖动。
有限脉宽作用:传输信号的脉冲宽度不可能是无限窄的a脉冲序列,因而其频谱在时钟附近带有一段倾斜的连续谱,其倾斜度随传输信息的内容变化而变化。这种时变的斜率将对定时信号进行相位调制,形成抖动。
限幅器的门限偏移:限幅器的门限会随温度的变化和元器件的老化而偏移。在这种情况下,当不同幅度的信号加到限幅器上时,将与门限的交叉点不再一致,使输出脉冲位置随输人信号的幅度而变化,而输人信号的幅度与传输信息的码型有关。
激光二极管的码型效应:在高比特率系统中,由于脉冲重复周期变短,激光二极管LD的有限通断时间对传输信号的码型(又称图案)的影响增大,而且这种影响随传输信号的码型不同而异,其结果导致码型相关抖动。
综上可知,光缆线路系统中的抖动源及其物理机制十分复杂,很难用精确的数学模型来描述。实际上,尽管各种不同机制的抖动源所引起的抖动谱是不一样的,但其差异仅表现在高频细节部分。经过多中继传输后,这些高频抖动分量均被滤除,只有低频分量才可能累积起来,进而对系统造成损伤。因此,、为了衡量光中继器各种抖动源所产生的抖动大小,更直接方法是测量。按照月前的技术水平,典型光中继器的随机性抖动均方根值为0.5°~1.5°,系统性抖动均方根值为0.5°~3.5°。总的抖动均方根值大约为1°~4°2。
理论模型在分析传统电缆数字线路系统抖动积累问题时,Chapman模型是广泛采用的分析模型。按照这一模型,在多中继链接的数字线路系统中,所有中继器都是线性时不变系统。对于由N个相同的中继器组成的线路系统,则第N个中继器的输出抖动功率谱密度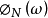 和输入抖动功率谱密度
和输入抖动功率谱密度 之间满足下述线性方程:
之间满足下述线性方程:
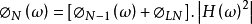
式中,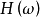 是中继器的抖动传递函数,
是中继器的抖动传递函数, 是中继器本身产生的抖动功率谱密度,它由随机性抖动分量
是中继器本身产生的抖动功率谱密度,它由随机性抖动分量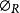 和系统性抖动分量
和系统性抖动分量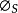 两部分组成。近来,Trischitta通过实验证明,Chapman的线性时不变模型原则上也适用于光缆数字线路系统。下面结合光缆数字线路系统的特点,叔lJ就三种不向类型的抖动积累进行分析。
两部分组成。近来,Trischitta通过实验证明,Chapman的线性时不变模型原则上也适用于光缆数字线路系统。下面结合光缆数字线路系统的特点,叔lJ就三种不向类型的抖动积累进行分析。
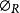 随机性抖动是指那些由各个中继器产生的、彼此互不相关的抖动分量。与传统分析方法不同,不仅将由噪声源和定时滤波器失谐所引起的抖动分量作为随机性抖动,而且也将码型相关抖动中彼此不相关的部分作为随机性抖动。因为尽管两者发生机理不同,但其积累规律是一样的。这里用表示总的随机性抖动功率谱密度。
随机性抖动是指那些由各个中继器产生的、彼此互不相关的抖动分量。与传统分析方法不同,不仅将由噪声源和定时滤波器失谐所引起的抖动分量作为随机性抖动,而且也将码型相关抖动中彼此不相关的部分作为随机性抖动。因为尽管两者发生机理不同,但其积累规律是一样的。这里用表示总的随机性抖动功率谱密度。
假设随机性抖动是均值为零的白色吧随机变量`由于各个中继器所产生的这种抖动是彼此无关的,于是经过N个相同的中继器后所得到的总的积累抖动均方值了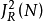 为
为

这一方程需用数值移分才能求解。但在下述两种虽然特殊却经常用的情况下,可以得到封闭解形式。
1、抖动传递函数为一阶低通滤波器函数形式
当定时滤波器采用单调谐电路亘失谐为零时,其相应抖动传递函数 可以表示为:
可以表示为:

式中B为抖动传递函数的3dB带宽。将式(3)代人式(2),经积分后可以得到封闭解如下:
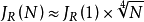
式中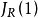 和
和 分别表示一个中继器和N个中继器的随机性抖动均方根值。累的随机性抖动均方根值随中继器数目的
分别表示一个中继器和N个中继器的随机性抖动均方根值。累的随机性抖动均方根值随中继器数目的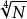 递增。
递增。
2、抖动传递函数为二阶低通滤波器函数形式
在高比特率光缆数字线路系统中,二阶低通滤波器是更常用的传递函数形式,其数学表达式为:

式中 表示阻尼系数,
表示阻尼系数,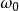 是抖动传递函数的3dB带宽角频率。这类传递函数可以用LC调谐电路、二阶锁相环或声表面波滤波器来实现。当阻尼系数示于0.707时,抖动传递函数的幅频特性出现大于0dB的最大值,称为抖动峰值。抖动峰值随
是抖动传递函数的3dB带宽角频率。这类传递函数可以用LC调谐电路、二阶锁相环或声表面波滤波器来实现。当阻尼系数示于0.707时,抖动传递函数的幅频特性出现大于0dB的最大值,称为抖动峰值。抖动峰值随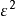 减小而增加。将式(5)代入式(2),可以得到封闭形式的解答如下:
减小而增加。将式(5)代入式(2),可以得到封闭形式的解答如下:


当中继器数目很大时,可以将上述公式进一步简化为:
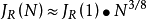

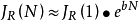
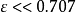
可见当阻尼系数很小时,随机性抖动可能随中继器数目的指数规律增长,而阻尼系数很大时,则仅随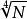 增长。为了控制抖动积累,应该取较大的阻尼系数`。这时,无论是一阶低通滤波器,还是二阶低通滤波器,抖动积累都随
增长。为了控制抖动积累,应该取较大的阻尼系数`。这时,无论是一阶低通滤波器,还是二阶低通滤波器,抖动积累都随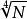 增长。
增长。
系统性抖动泛指各个中继器所产生的彼此完全相关的抖动。一般文献认为,系统性抖动就是码型相关抖动。实际各个中继器定时电路的缺陷不会是完全相同的,信号脉冲形状也有差异,因而码型相关抖动可以分解为两个正交分量:一项为码型全相关的抖动,称为系统性抖动,另一项是码型不相关的抖动,其特性如同随机噪声一样,因而可以归人随机性抖动。这样,由于各个中继器所产生的系统性抖动的功率密度谱沪,应按线性叠加,积累的抖动均方值为:

可见,积累的系统性抖动不仅跟抖动传递函数的幅频特性有关,而且还跟相频特性有关。这一点跟随机性抖动不同。
1、抖动传递函数为一阶低通滤波器函数形式。
将式(3)代人式(2)积分可以得到:

利用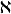 函数及其递推公式和近似展开式,可以将上式进一步简化为:
函数及其递推公式和近似展开式,可以将上式进一步简化为:
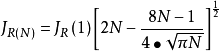
该式最大误差仅1.4%,特别是N值不太大时,比Byrne采用Sitrilgn公式所得到的近似公式精度要高。`当N>=100时,则有
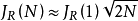
可见,积累的系统性抖动均方根值大致随杯了关系增长,其速率比随机性抖动要快得多了。
综上所述,当抖动传递函数没有峰值时,无论采用一阶低通滤波器,还是二阶低通滤波器,积累的系统性抖动都随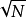 关系增长,比随机性抖动要快得多、但是,当抖动传递函数出现峰值时,则系统性抖动也近似按中继器数目的指数规律递增,只不过积累速率不如随机性抖动那么快2。
关系增长,比随机性抖动要快得多、但是,当抖动传递函数出现峰值时,则系统性抖动也近似按中继器数目的指数规律递增,只不过积累速率不如随机性抖动那么快2。
目前,已发表的有关实际光缆线路系统的抖动积累测试数据不多,`所得结果也差异甚大。事实上,:影响抖动积累规律的因素很多,诸如中继器数目、定时滤波器类型、传输信号的线路码型和抖动传递函数形纽贷等等。实际系统的这些参数千差万别,不可能用一个统一简单的规律来概括这些影响。但是,就长途光缆数字线路系统而言,下述的几个特点是值得注意的:
随机性抖动的影响不容忽视与传输电缆数字线路系统相比,光缆系统不仅增加了一些特有的随机性抖动源,而且在码型相关抖动中大约有50%的分量也属于随机性抖动,这就使得随机性抖动在总的抖动量中所占的比重增加。特别是,当抖动传递函数有峰值时,随机性抖动的积累速率甚至会超过系统性抖动,成为主要的部分。
码型相关抖动不一定按系统牲抖动积累如前所述,各个中继器所产生的码型相关抖动并非完全相关。实测结果表明,仅有50%是全相关的,仍按系统性抖动积累,而剩余的50%是完全不相关的,只能按随机性抖动积累处理。在一个由光缆系统组成的数字段内,抖动积累效应将有所减弱。
数字段内总的抖动积累效应有所减弱这是因为数字复用设备中备有独立的振荡器产生时钟,所以前一个数字段的抖动一般不能进入本数字段,这样,抖动主要在一个数字段内积累。而另一方面,在传统电缆线路系统中,中继器间隔只有几km,而光缆系统可达几十km,因而对于一个280km的标准数字段来说,只含有几个中继器。显然,中继器数目的大大减少意味着抖动积累效应的减弱。这有利于整个系统抖动性能的改善。
 总之,在一个设计良好的光缆系统中,抖动积累一般不会简单地遵循传统的
总之,在一个设计良好的光缆系统中,抖动积累一般不会简单地遵循传统的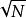 规律,而是处于
规律,而是处于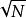 和
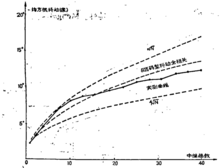
和 之间。当然,由于实际系统情况千差万别,得到不同的积累规律不足为怪。图给出最新发表的美国ATT公司280Mb/s单模光缆系统抖动积累测试结果。
之间。当然,由于实际系统情况千差万别,得到不同的积累规律不足为怪。图给出最新发表的美国ATT公司280Mb/s单模光缆系统抖动积累测试结果。
由图中实测曲线可见,当中继器数目少于10时,抖动积累按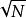 递增。而大于10以后,抖动积累逐渐偏离
递增。而大于10以后,抖动积累逐渐偏离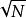 关系,处于
关系,处于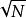 和
和 之间。采用修改的chapman模型(如图中间虚线)后,则计算结果与实测曲线比较吻合。因而,在系统分析时,我们可以采用修改的chapman模型来估算抖动积累特性2。
之间。采用修改的chapman模型(如图中间虚线)后,则计算结果与实测曲线比较吻合。因而,在系统分析时,我们可以采用修改的chapman模型来估算抖动积累特性2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国