[科普中国]-黏性阻力

计算方法边界层理论计算概述

影响边界层厚度的主要因素有：来流速度u、距板前单点O的距离x和流体的黏性（运动黏性系数）v。边界层厚度取决于有这三个物理量所组成的无量纲数：Rex=vx/u

1、积分法：以边界层的动量积分方程为基础，但遇到的困难是无法求出边界层内的速度分布，往往在计算之前先假定某种速度分布形式。

2、微分法：直接求解边界层的偏微分方程，但在求解时须引进所谓湍流模式来定量描述雷诺应力项。

N-S方程理论计算概述运用N-S方程理论计算黏性阻力时，应注意

1、由于RANS方法本身并不封闭，须引进所谓湍流模式来定量描述雷诺应力，能否正确给出湍流模式至关重要。

2、数值计算的方法和技巧。离散方法选取是否适当、网格划分是否恰当以及计算网格的自动生成在数值计算至关重要。

减阻方法当黏性流体(水、空气、原油等) 沿一固定边界流动时，不论是内流(如管流) 或外流(如黏性流场中运动的物体)，边界上的流速u均等于零，边界面上的法向速度梯度du/dy则不等于零，所以存在流体对边界的剪力τo.这边壁剪力做功的结果就要消耗掉流体中的一部分机械能，并最终以热量形式向周围发散，逸散于流体。 因此，降低黏性阻力就是减少机械能的消耗，也就意味着节能。1

长期以来，从航空到水下运动的广阔领域，人们一直在寻找减少流体阻力的有效方法。减小黏性阻力，大体有以下四种作法：1、用任何一种减小壁面剪切应力的方法来减小摩阻；2、作成浸水面积小、摩阻形状影响系数小的形状；3、 表面作得光滑以减小粗糙度的影响；4、防止边界层分离以减小压力阻力。

为了实现这些作法， 举出下列一些方法

（1）利用物体形状保持层流流动

（2）移动表面

（3）吸入流体保持层流流动

（4）均匀喷出流体

（5）利用空气膜

（6）弹性表面

（7）利用聚合物等添加剂

（8）利用物体形状减小浸水面积

（9）利用物体形状减小摩阻形状影响系数

（10）利用光滑表面减小粗糙度的影响

（11）利用物体形状防止端流分离

（12）利用吸入或喷出流体防止分离

（13）利用涡旋发生器或粗糙度防止分离

（14）利用变流板防止分离

（15）利用整流板控制分离

（16）磁流体力学控制边界层

（17）表面加热

（18）表面涂膜2

其中研究较为深入的方法有以下几种：

(1)探索物体的流线型，包括由于形体改变对保持层流边界层的影响。希望通过型线的选择，能“自动”保持边界层层流流态，如果做不到这一点，则通过吸气、增压或其它方法“强制”保持它3。

(2)随着流体力学和高分子化学研究的进一步发展，众多学者提出高分子稀溶液能实现黏性减阻。即当把高分子稀溶液注入物体壁面附近时(注入到流核区无效)，就内流而言，最高时可使阻力系数减少40%～50%，这在各领域已有了一定的应用。但这种减阻的方法在应用时有一定的局限性，有的情况甚至是不可能的，如船舶的黏性减阻就无法通过在水中加高分子稀溶液达到目的4。

(3)根据仿生学的启示，人们发现弹性材料护面可实现黏性减阻。有实验表明:游泳运动员游泳时穿紧身的弹性尼龙衣，比不穿游泳衣时所受的阻力要小。减阻的主要原因是此弹性边界为柔顺边界，最理想的情况下，边界的波动能自动与附面层的波动合拍，即所谓的同步波动，在这种情况下，流动阻力大大降低，可实现最大减阻。当然，同步程度的不同，传递的能量在边界区域直接散失的能量也不同。

工程实际简介当船体运动时，由于水的粘性，在船体周围形成“边界层”，从而使船体运动过程中受到粘性切应力作用，亦即船体表面产生了摩擦力，它在运动方向的合力便是船体摩擦阻力。另外由于水具有粘性，旋涡处的水压力下降，从而改变了沿船体表面的压力分布情况，这种由粘性引起船体前后压力不平衡而产生粘压阻力。因此，粘性阻力由摩擦阻力和粘压阻力两部分组成，它与船体的形状和雷诺数密切相关。

由于船体形状比较复杂，用理论精确计算船体的摩擦阻力尚不能付诸工程实用，为此船舶工程中仍不得不沿用傅汝德提出的相当平板假定，即船体的摩擦阻力与同速度、同长度、同湿面积的平板摩擦阻力相等。这一假定是计算船体摩擦阻力的基础。

平板边界层假设顺着流动方向放置一薄平板，水流以均匀速度υ流经平板，如图所示。当水流过平板时，由于水具有粘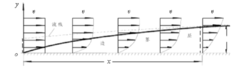性，故平板表面处的水质点均被吸附在平板上，平板表面上流速为零。随着与平板表面距离y 的增加，流速逐渐增加，当y 增至某一距离δ 时，其处流速达到来流的速度值。我们称存在粘性作用的这一薄层水流为边界层，δ 是纵向位置x的函数，称为界层厚度。在相应平板各处距离为δ 的点，可连成一界面，此界面称为界层边界。

应当指出，一般定义边界层厚度常以界层内流速达到99%来流速度作为界层的边缘，该处与板面的距离作为界层厚度值。根据实验测定，影响边界层厚度的主要因素是流速υ、距板前端点o的距离x和流体的粘性，即运动粘性系数ν。进一步的实验指出δ取决于由这三个物理量所组成的无量纲数Rex=vx/u，即局部雷诺数。如果υ，x一定，当Rex很大时，则表示流体的粘性作用很小，δ就很小。理想流体可视为运动粘性系数ν = 0的实际流体，其雷诺数Re=∞，边界层厚度δ = 0。

对边界层内的流动状态进行观察研究，发现边界层内存在两种流动状态：在平板前端部分，水质点表现有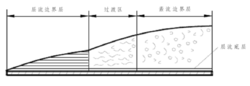稳定的分层流动，边界层沿板长方向增长较慢，这种流动状态称为层流。而在平板后部，水质点互相碰撞，运动方向极不规则，但其平均速度还是沿平板方向前进，界层厚度沿板长方向的增长较层流情况为快，这种流动称为紊流(又称湍流)。实际上在层流和紊流之间还有一段过渡状态称为过渡流或变流，如图所示。

层内的流动状态完全取决于平板的局部雷诺数Rex：

层流状态：Rex