[科普中国]-弯曲应力

基本概述

在载荷作用下，梁横截面上一般同时存在剪力和弯矩。由切应力τ构成剪力，由正应力σ构成弯矩，如图1所示。由正应力与切应力引起的弯曲分别称为弯曲正应力与弯曲切应力。1

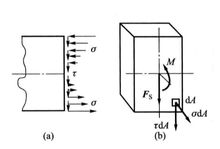
弯曲正应力的一般公式推导纯弯曲梁横截面的正应力公式，与推导扭转切应力公式相似，也需要从变形儿何关系、物理关系和静力学三方面来考虑。1

变形几何关系纯弯曲时梁的纵向“纤维”由直线变为圆弧，相距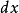的两横截面1'－1'和2'－2'绕中性轴发生相对转动，如图2所示。横截面1'－1'和2'－2'延长相交于O点，O点即为中性层的曲率中心。设中性层的曲率半径为ρ，此两横截面夹角为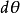，则距中性层为y处纵向“纤维”ab的正应变为

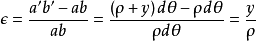
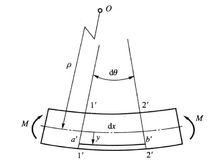
实际上，由于距中性层等远各纵向“纤维”的变形相同，所以，上述正应变ε即代表距中性层为y的任一纵向“纤维”的正应变。

物理关系根据单向受力假设，各纵向”纤维”处于单向拉仲或压缩状态，因此，当正应力不超过材料的比例极限时，胡克定律成立，由此得横截面上距中性层y处的正应力为

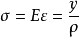
该式就是梁纯弯曲时横截面上的正应力分布规律。由此式可知，横截面上任一点处的正应力与该点到中性轴的距离成正比，距中性轴等远的同一横线上的各点处的正应力相等，中性轴各点处的正应力均为零。

静力学关系上面虽已得到正应力分布规律，但还不能用所给公式直接计算梁纯弯曲时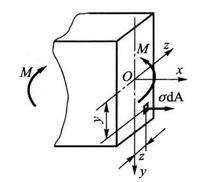横截面上的正应力。至此有两个问题尚未解决：一是中性层的曲率半径ρ仍未知；二是中性轴位置未知，故式中之y还无从确定。解决这两个问题，需要借助于静力学关系。

令横截面纵向对称轴为y轴，中性轴为x轴，梁轴线为x轴，在坐标（y，a）处取一微面积dA，法向微内力为ρdA（图3），横截面各微面积上的法向微内力ρdA组成一空间平行力系，而且横截面上不存在轴力，仅存在位于x－y平面内的弯矩M，因此

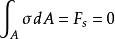
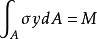
得：

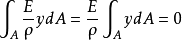
由于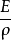≠0，故

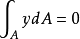
式中左边的积分代表横截面对z轴的静矩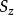。只有当z轴通过横截面形心时，静矩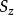才为零。由此可见，中性轴通过横截面形心。
可得：

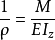
此式为用曲率表示的弯曲变形公式。公式中代表横截面对z轴的惯性矩。
由推出的公式易得纯弯曲时梁横截面上的正应力计算公式为：

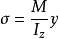
此式为弯曲正应力的一般公式。

弯曲正应力公式的应用范弯曲正应力公式是在纯弯曲情况下推导的。当梁受到横向力作用时，在横截面上，一般既有弯矩又有剪力，这种弯曲称为横力弯曲。由于剪力的存在，在横截面上将存在切应力τ，从而存在切应变γ=τ/G。由于切应力沿梁截面高度变化，故切应变γ沿梁截面高度也是非均匀的。因此，横力弯曲时，变形后的梁截面不再保持平面而发生翘曲，如图4中的1-1截面变形后成为1'-1'截面。既然如此，以平面假设为基础推导的弯曲正应力公式，在横力弯曲时就不能适用。但是，如果两截面间没有载荷作用时，则两截面的剪力相同，其翘曲程度也相同，由弯矩所引起的纵向纤维的线应变将不受剪力的影响，所以弯曲正应力公式仍然适用。当梁承受分布载荷作用时，两截面上的剪力不同，因而翘曲程度也不相同，而且，此时纵向纤维还受到分布载荷的挤压或拉伸作用，但精确分析表明，如果梁长l与梁高h相比足够大时，这种翘曲对弯曲正应力的影响很小，应用公式计算弯曲正应力仍然是相当精确的。

综上所述，对于各横截面剪力相同的梁和各横截面剪力不相同的细长梁，在纯弯曲情况下推导的弯曲正应力公式仍然适用。