[科普中国]-合力矩定理

基本概念

合力矩定理：在平面汇交力系中，合力对平面内任意一点的力矩，等于其所有分力对于同一点的力矩的代数和。由公式可以表示为：

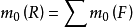
力矩力矩的作用是使物体绕点或轴转动，单位是牛·米（N·m）或千牛・米（kN，m）。1

力矩具有以下几点性质：

1）在平面同题中，力F对0点之矩不仅取决于力F的大小和方向，同时还与矩心0的位置有关，矩心的位置不同，力矩的大小和转向也不同，因此，力矩必须与矩心相对应，即指明矩心的位置，矩心的位置通常用符号 中的下标“0”来表示，不指明矩心来谈力矩是没有意义的；

2）在特殊情形下，当力的大小等于零，或力的作用线通过矩心（即d=0）时，则力矩等于零；

3）当力F沿其作用线移动时，它对任一点之矩不发生变化，因为这时力F的大小和方向以及力臂d均未改变；

4）互成平衡的两个力对任一点之矩的代数和恒等于0，因为此二力对任一点之矩大小相等，转向相反。

必须指出，力矩的感性概念是通过力使刚体绕固定点（或固定轴）转动而引出的，但当抽象为具有普遍意义的概念后，作用于刚体上的力可以对刚体上任意一点取矩。即矩心不一定非要取在可以使刚体绕之转动的固定点（或固定轴）上，而是可以取刚体上任意一点为矩心，对于非自由刚体，力对其上任意一点取矩时，刚体并不一定就绕该点转动，但定有转动趋势，例如，用坂手挖紧螺后，继保持用于坂手上的力，虽说螺帕和板手都不转动了，但力矩却仍然存在。

合力矩定理的证明设有平而汇交力系 ， ，…， ，其合力 ，如图1所示，在力系所在平面内任取一点0为矩心，以0点为原点，作直角坐标系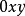 ，井使x轴通过各力的汇交点A。力 ， ，…， ，和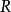 在y轴上的投影分别为 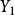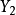， ，…， 和 。1

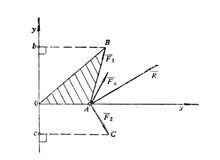
由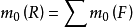

得力 对0点之矩

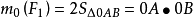
其中线段0b是力 在y轴上的投影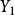，因此，上式又可写为

同理可得

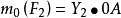
根据合力投影定理，有

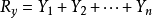
上式两边同乘以0A，得

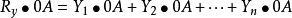
即：

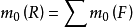
合力矩定理虽然是从具有合力的平面汇交力系导出的，但是也适用于有合力的其它力系。