基于时空序列信息的电网扰动传播特性量化评估方法

摘要

本文阐述了电网扰动传播特性，介绍了扰动传播特性机理，以及该领域研究现状。基于 K-means 聚类算法，提出了一种轨迹驱动的电网扰动传播特性量化评估方法。利用该方法针对 IEEE 39 节点系统进行扰动传播分析，并探讨了扰动传播分析的未来研究方向。

关键字

电网；扰动传播特性；时空轨迹序列；向量轨迹距离；量化评估

0 引言

随着人类的经济活动到了工业经济时代，对电力系统的稳定运行提出了更高要求。电网的扰动不可避免，但若能在扰动向其余区域传播初期即采取措施，则能在一定程度上降低可能带来的巨大损失，提高系统稳定性。随着电力系统的发展，电网时空分布特性日趋复杂，对电网扰动传播的准确评估也变得更加困难。

现有的对于电网扰动的研究主要包括扰动定位、扰动分类和扰动传播分析三部分。针对扰动定位和扰动分类问题的研究较为活跃，学者们提出了基于数据驱动和基于模型驱动的两大类方法，并已有很多较为成熟的算法；而扰动传播分析的相关研究则较少，都是针对各自定义的指标来分析扰动对各节点影响程度，尚无统一量化定义。

本文以电网扰动传播分析为主题，探讨了电网扰动传播特性机理；利用电网时空序列信息，基于K-means 聚类算法，提出了一种轨迹驱动的电网扰动传播特性量化评估方法，并借助连续潮流构建扰动数据集，采用该方法对 IEEE 39 节点系统的扰动传播进行深入分析。

1 电网扰动传播特性机理

电力系统在运行中常常会受到各种随机扰动的影响。扰动所引起的局部状态量的偏移将以机电波的形式向其他区域传播，从而导致其余地区电网状态量的改变，进而影响电网安全稳定运行。在模型驱动的扰动传播分析上，James Thorp 等将发电机、线路视为电网的基本元件，在电网规模无限大、发电机间距可忽略的假设下，提出电网连续体模型的建模方法，推导得到机电扰动传播速度和惯量的关系

其中，v 为机电扰动传播速度；ω 为发电机角频率；U 为电压幅值标幺值；θ 为线路阻抗角；z 为线路单位阻抗标幺值；h 为单位长度惯量。

虽然相比数值解，解析解更能反映各状态量之间的关系，进而反映扰动传播特性。但是，由于实际电网的参数空间分布规律复杂，难以得到电网扰动传播方程的解析解，现有的基于模型驱动算法大多进行了一些简化和假设，这便使模型法分析结果难以准确反映电网的真实情况。

近年来，各种基于数据驱动的算法也逐渐应用于电网故障扰动传播分析，如将生物学中成熟的传染病模型应用于电网扰动传播动力学模型的构建，从而揭示扰动发生后受扰动节点密度变化情况。随着人工智能技术的发展，许多基于机器学习的方法也被陆续提出，如利用卷积神经网络或循环神经网络实现对电网故障的定位、分类等任务。但是，当今大电网规模不断发展并且结构日益复杂，人们对于电网扰动传播特性机理的认识还远远不足，这一领域的研究尚需完善。

2 基于电网时空序列信息的扰动传播特性

分析考虑到扰动在电网中的影响常常具有很明显分布特性，针对扰动对节点状态量的影响，本文提出的轨迹驱动的电网扰动传播特性量化评估方法，采用 K-means 聚类算法对电网时空序列信息进行挖掘分析，通过聚类结果分析扰动对电网不同节点的影响程度。

在电网运行过程中，通过量测可以得到每个时间段面下的发电机、节点、支路和负荷的状态信息，本文所提方法针对节点状态信息进行聚类分析，进而对电网扰动传播特性进行分析。在一个具有 n 个节点的系统中，将一段时间内每个节点在每个时间断面下的电压幅值（U）和电压相角（A）分别视为一组时间序列，即可得到n组电压幅值序列和 n 组电压相角序列，通过进一步计算可得到对应的电压实部（SB）序列和电压虚部（XB）序列，从而可将各节点的电压实部、虚部数据在二维空间中表示。

其中，K 为总时间断面数；SBi 为节点 i 对应的电压实部序列；XBi 为节点 i 对应的电压虚部序列。在此基础上，设置合适的簇数量，利用 K-means算法对除平衡节点和受扰动节点之外的所有节点进行聚类，进而将扰动对节点的影响进行量化评估。

3 仿真算例

连续潮流是研究电压稳定分析的一种有力工具，它克服了常规潮流计算中雅可比矩阵奇异 , 从而导致潮流方程难以收敛的问题。在连续潮流中，针对某一种组合模式下的发电和负荷，按照某一固定模式不断增加，直到达到功率传输的极限，并可绘制出完整的PV曲线，以反映系统随着负荷变化而引起的节点电压的变化。连续潮流可视为一种对电网添加扰动的场景，因此本文利用连续潮流构建扰动传播数据集，并针对该数据集对扰动传播特性进行分析，具体的算法流程如图1所示。

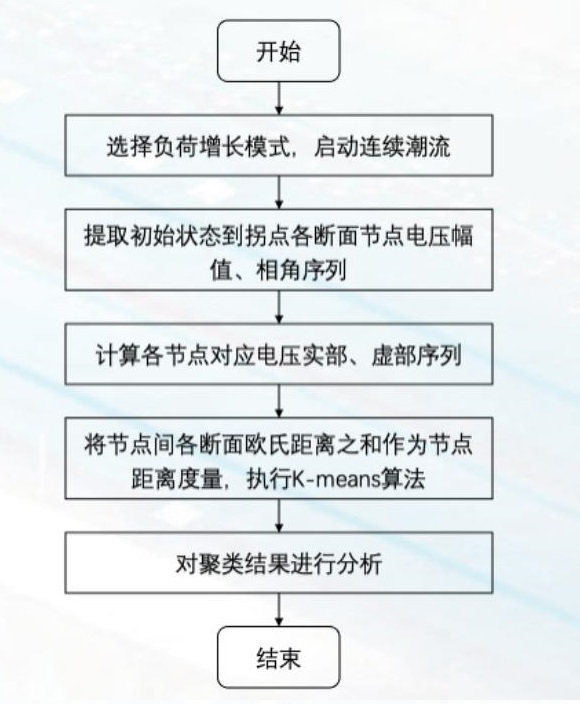
图 1 算法流程图

以 IEEE39节点系统为例，图2为39节点系统拓扑图，其中31号节点为平衡节点。在连续潮流中，将IEEE39节点系统标准算例数据作为初始状态，随机选取三个较分散的有代表性节点，本文选取 4、15、23 三个节点，共进行三组实验。① 不断增加 4节点负荷，直到达到PV曲线的拐点，得到624个断面；② 同理增加15节点负荷，得到937个断面；③ 同理增加23节点负荷，得到1349个断面。

图 2 IEEE 39 节点系统拓扑图

对于三种扰动下得到的电压幅值和相角序列，计算每种扰动下各节点的电压实部、虚部序列，图3为分别绘制的39个节点电压实部、虚部轨迹图。可以看到，受扰动的节点电压相角变化很大，因此其轨迹图在整体中较为突出，且不同节点的轨迹图呈现很明显的区域集中性。

本文利用第2章提到的方法，采用 K-means 算法对每种扰动下的37个节点（除受扰动节点和平衡节点）的电压轨迹进行聚类，在此，簇数量均设置为3，并进行了100次迭代，并分别对每种扰动下三个簇中37个节点和受扰动节点的电压实部、虚部轨迹用不同颜色着色以展示聚类效果。如图4所示，聚类效果比较理想，如对于15节点受扰动的情况，被15节点分隔的上半部分节点全部被聚为一个簇，下半部分节点也较好的被划分为两个簇。

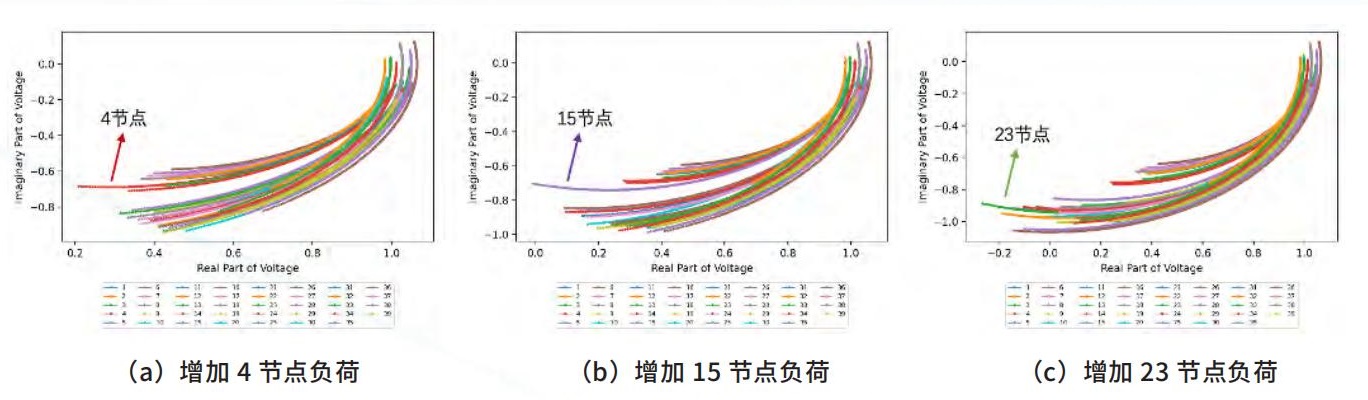
图 3 三种扰动下 39 个节点电压轨迹图

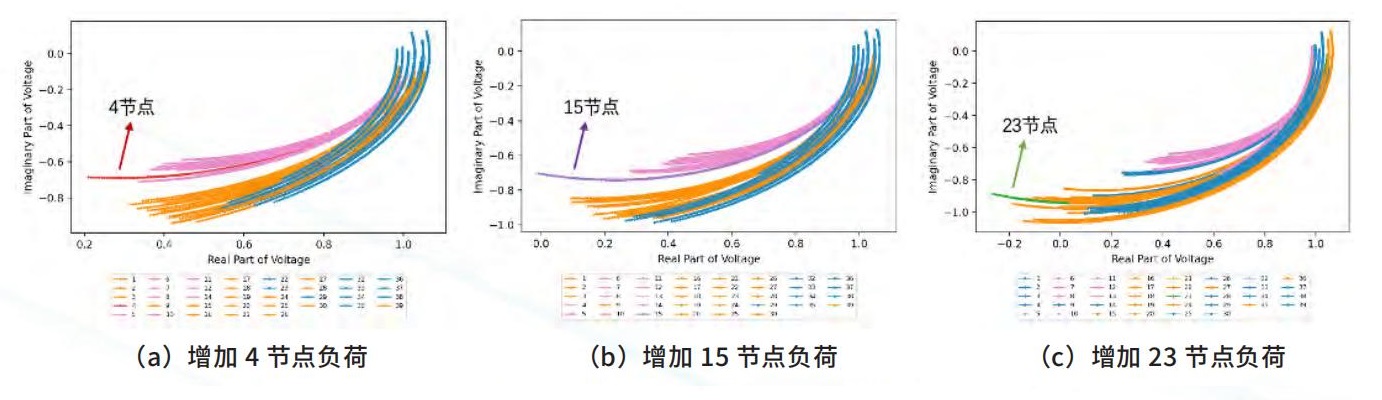
图 4 三种扰动下对电压轨迹聚类结果

为进一步分析扰动传播范围，每种扰动下，在拓扑图中对三个簇中节点用不同颜色进行着色以实现可视化，结果如图5所示。通过对比观察图4和图5中三组实验结果，可以得到下述结论。

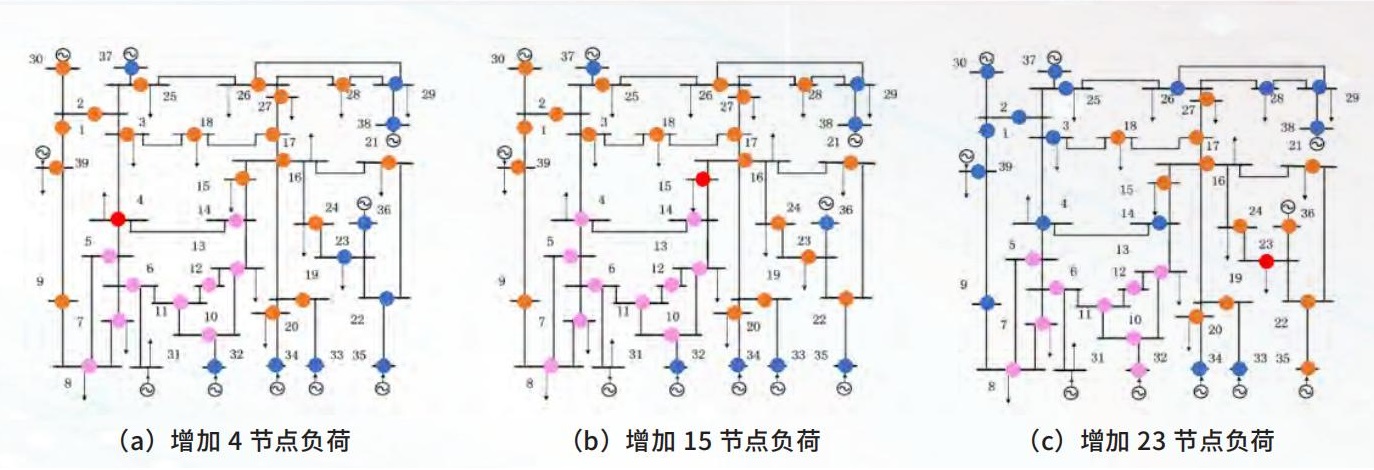
图 5 三种扰动下电压轨迹聚类结果在拓扑图中的可视化

（1）无论扰动发生在何处，粉色簇中包含的节点几乎相同，这些节点全部分布在平衡节点周围，电压幅值变化很大，而电压相角变化很小。

（2）橙色簇中包含的节点主要分布在扰动节点附近，这些节点电压相角变化很大，仅次于受扰动节点，但电压幅值变化很小。

（3）蓝色簇中包含的节点主要为发电机节点和离受扰动节点较远的部分节点，这些节点电压幅值、相角变化都比较适中，受扰动影响相对较小。

（4）由于电网复杂的内部机理，扰动对其余节点的影响虽然具有很强的区域集中性，但并非从受扰动节点均匀向各个方向传播，如 15 节点受到扰动后，一侧受平衡节点影响电压幅值变化较大，而另一侧电压相角变化较大。

此外，本文中仅将簇个数设置为3，得到了较为粗糙的聚类结果，若进一步设计更好的聚类算法，将节点划分为更多个簇，即可更清晰地将受扰动影响大的节点缩小到较小范围，从而更有助于评估扰动对不同区域的影响程度。

4 结束语

本文在介绍电网扰动传播机理及研究现状的基础上，基于 K-means 聚类算法，提出了一种轨迹驱动的扰动传播特性量化评估方法。借助连续潮流，在IEEE39节点系统标准算例的基础上制造数据集，通过添加不同位置的扰动，利用该方法获得了IEEE39节电系统中的扰动传播特性。本文提出的分析方法重点从时间序列的相似性上进行了初步探讨，针对电网特性设计更好地聚类算法，特别是对电网的拓扑连接与节点间的空间约束进行深入考虑，有助于准确评估扰动的影响范围。

此外，研究电网扰动传播特性机理具有重要的实际意义，基于数据驱动的方法具有很强的泛化能力，且样本数据足够时可以达到很好的性能，但缺乏一定的可解释性；基于理论驱动的方法具有很强的解释性，但随着电网规模的增大以及各种不确定因素的引入，理论建模变得十分困难，因此，在针对大电网扰动传播分析中，数据驱动和理论驱动相结合的方法值得进行深入研究。

（参考文献略）

选自《中国人工智能学会通讯》

2021年第11卷第11期

智慧能源专题