中国科大展示复杂系统随机建模的信息存储量子优势

近日，我校郭光灿院士团队与曼彻斯特大学、南洋理工大学合作，利用量子技术在复杂系统随机建模中的信息存储方面取得重要进展。该团队李传锋教授和项国勇教授与合作者使用单个量子比特的内存实现的量子模型可以获得比相同内存维度的任何经典模型更高的精度。该研究成功展示了量子技术在复杂系统非马尔科夫过程建模中的存储优势。该工作以“Implementing quantum dimensionality reduction for non-Markovian stochastic simulation”为题于5月6日在线发表于Nature Communications。

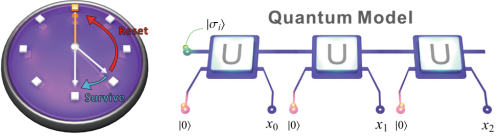
图1 实验中进行量子模型模拟的经典时钟过程概念图；基于酉操作的量子模型线路图

从化学反应到金融市场，从气象系统到星系形成，人们需要处理各种规模的复杂过程。随机建模能够帮助我们预测这些过程的未来行为。然而，由于这些随机过程通常是非马尔可夫的，其未来行为不仅取决于当前状态，也基于它的过去状态。为了模拟这样的过程，必须有一个存储器来存储系统的大量的观测信息。信息存储量将直接和预测未来行为的精度关联，因此，这在实践中将导致一个瓶颈，需要在减少内存与预测准确性之间进行权衡。

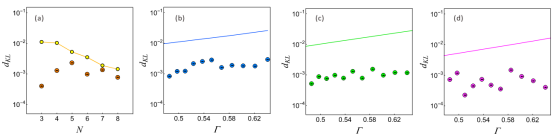
图2 实验结果图：实验实施的量子模型的精度与经典模型的理论极限精度。该精度用概率分布的距离dKL衡量，图（a-d）展示的是不同参数下的理论与实验结果

项国勇教授研究组发现即使在对纯经典动力学过程建模的时候，量子技术也可以展示出显著优势。该团队基于光子系统实验实现了一系列非马尔可夫随机过程的量子模型（如图1所示）。该类随机过程具有一个可调参数，用于控制其有效的内存长度，最优经典模型的内存维度随此参数的值而增长。实验证明，量子模型可以仅使用单个量子比特作为内存来模拟该类行为中的任何过程（即任意该参数），并且即使存在实验噪声，此量子模型也比最优的相同内存维度的经典模型能够更准确地做出未来行为的预测（如图2所示）。

Nature Communications编辑对本工作小结为：“Quantum technologies allow memory advantages in simulating stochastic processes, but demonstrating this for non-Markovian processes (where the advantage would be stronger) has been missing so far. Here the authors fill this gap analytically and experimentally, using a single qubit memory to model non-Markovian processes（量子技术在模拟随机过程中拥有存储优势，但是在非马尔科夫过程（该过程的量子优势更强）中的实验验证一直没有实现。本文的作者利用单比特存储实现非马尔科夫过程的建模，通过理论分析和实验验证填补了这一空白）。”总体而言，该工作是朝着展示这种量子记忆优势的可扩展性和鲁棒性迈出的关键一步。