抽奖也有心理学？进来看看你中奖的概率有多大

彩票、游戏抽卡，各类抽奖活动充斥着我们的生活。对于举办抽奖活动的商家来说，花哨的抽奖活动可以高效地招来客源；而对于参加抽奖活动的消费者来说，较小的投资就有概率获得丰厚回报的活动着实非常诱人。

但在参加抽奖活动时，你是否也会有疑惑：“奖品那么多，好多人都中奖了，为什么只有我从来没有抽到过？”

当然，抽不到奖并不排除黑心商家暗箱操作的可能，但今天我们要探究的是公正抽奖中的心理学与概率问题。

你为什么总感觉自己能中奖？

需要明确的是，生活中大部分抽奖活动的中奖概率都是很低的。

举个简单的例子，经常玩手游的朋友可能很清楚，抽到稀有角色的概率一般都在2%以下；而常见的彩票游戏机制“双色球”，中奖概率仅为6.71%（以福彩双色球为例，单式投注1注，包括一等奖至六等奖）。

至于“超级大奖”的一等奖，中奖概率只有大约一千七百万分之一，当然双色球还有复式投注等规则，我们这里只做简单举例。

由此可见，中奖的人，都属于人群中的“少数幸运儿”。

既然中奖概率这么低，中奖人数这么少，为什么我们又会感觉周围人都在中奖呢？这一点需要从心理学的角度去考虑。

首先，抽奖的举办方为了吸引更多人前来抽奖，会利用中奖的人进行宣传，而各路媒体也特别乐意报道中了大奖的幸运儿，这就导致我们的注意力集中在了中奖的少数人身上，忽视了广大未中奖的参与者，让我们产生了“人人都在中奖”的错觉。

这种逻辑谬误，在心理学上被称为幸存者偏差（Survivorship Bias），即人们只看到了经过某种筛选而产生的结果，并未意识到筛选的过程，因此忽略了被筛选掉的信息。

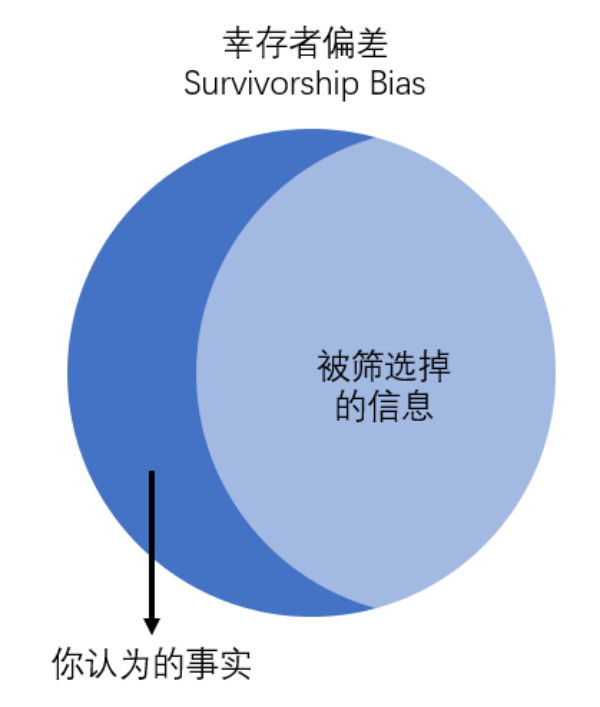
（图片来源：作者自制）

经过商家和媒体的筛选，我们只关注到了中奖的人，却没有关注到广大未中奖的人，从而忽略了“中奖概率很低”这个事实。

其次，作为抽奖的参与者，我们主观上希望自己中奖。所以，我们通常会将更多注意力放在中奖者身上，刻意忽视未中奖者的存在。

而这种思维误区，被称为确认偏误（confirmation bias，也称证实性偏差、验证性偏见），即我们在判断自己的假设并作出决策时，通常会觉得支持性的论据更具说服力，同时还会有意或无意地寻找与自己假设一致的信息，而忽视可能与之不一致的信息。

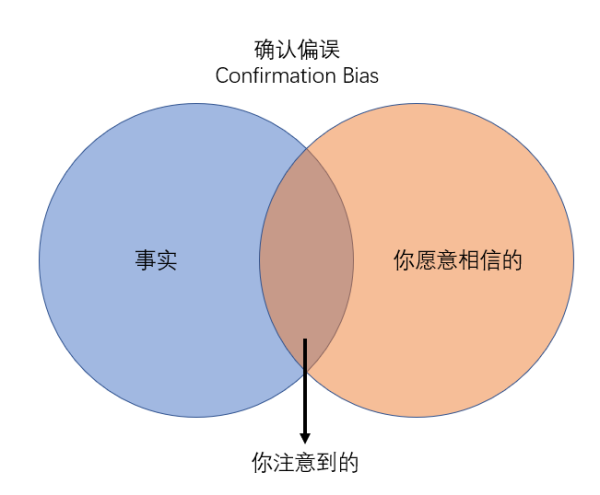
（图片来源：作者自制）

简单地说，就是“我们总是趋向于相信我们想相信的”。

在抽奖中，我们假设自己会中奖，接着，大脑就会持续地筛选支持我们假设的证据（少数中奖者），而选择性地忽略对我们的假设产生威胁的证据（大多数未中奖者），从而在主观层面忽视了“中奖概率很低”的事实。

抽奖的先后顺重要吗？

在抽签、摸奖这类抽奖活动中，因为带奖的奖券数目有限，很多人会担心抽奖时，要是奖券先被别人抽走了，后抽的人就抽不到了，所以后抽的人中奖概率会比先抽的人低。但事实真的是这样吗？

（图片来源：作者自制）

让我们先来明确一下概率中的基本概念。

首先是随机试验，即对于一个试验，如果在一定条件下该试验可重复，结果不止一个，并且每次试验时，我们不能肯定是哪一个结果出现，这样的试验就被称为随机试验。在随机试验中，最基本且不能再分的结果被称为基本结果或基本事件。

对于抽奖，我们无法确定每次抽奖抽到的是哪张奖券，所以这个抽奖活动就是一个随机事件，而抽到的每一张奖券则分别为一个基本事件。

此外，抽奖活动还属于古典概型，即基本事件的个数有限且可能相等。对于古典概型，我们有某一事件A发生的概率=A包含的基本事件的个数 基本事件的总数。

接下来是条件概率，即事件A在事件B发生的条件下发生的概率，表示为P(A|B)，当只有AB两个事件时，P(A|B)=P(AB)/P(B)，变形可得P(AB)=P(A|B) P(B)。

我们还是从例子入手来分析这个问题。

假设某次抽奖活动中共有10张券，其中1张奖券。那么根据古典概型，第一次抽奖共有10种可能的结果，其中一种结果为中奖，所以第一次抽奖抽中奖券的概率就是P(A)=1/10（记抽中奖为事件A，抽不到记为事件a，第二次抽到记为事件B）。

第二次抽奖中，根据第一次抽奖的结果不同，分为两种情况：

1. 第一次抽到了奖券，奖池中剩余9张不带奖的券。

2. 第一次未抽到奖券，奖池中剩余9张券中有1张带奖。根据古典概型，显然此时抽到奖券（记为事件C）的概率为1/9。

需要注意的是，在第二种情况下计算得到的概率，实际上是条件概率。即在第一次没有抽到奖券的条件下，第二次抽到奖券的概率，记为P(C/a)=1/9，并不是第二次抽到奖券的真实概率P(B)。

我们如果想要第二次抽奖抽到奖券，则需要情况2出现并且抽到奖券，即事件a和事件C同时发生，记作P(B)=P(Ca)，由我们之前介绍的条件概率公式，可得：

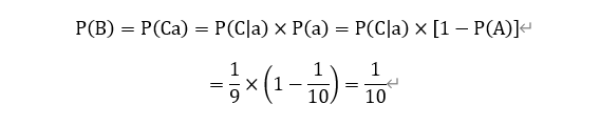
所以，可以得出结论P(A)=P(B)，即第一次抽奖和第二次抽奖抽中的概率相同。

以此类推，将抽奖之前中奖/未中奖笼统地归为两个事件，运用这种方法，我们可以拓展到第三，乃至第十次的抽奖。你会发现，每次中奖的概率都是相同的。

所以，在顺序抽奖中，先抽和后抽，中奖概率都是一样的。

遇上蒙特难题该怎么选？

蒙特难题是概率学中和抽奖有关的非常有趣的问题，也被俗称为“羊车门问题”，大概内容如下：

你参加了一档电视节目，在你的面前有三扇门，其中一扇门后面是一辆轿车，而剩下两扇门后分别是一只羊。

主持人关闭了这三扇门，让你选择其中一扇，如果你选择的门后是轿车，这辆车就是你的了，但如果你选择的门后是羊，你将无法获得任何东西。

在你做出了自己的选择后，知道轿车位置的主持人为你打开了剩下的两扇门中的一扇，而门后是一只羊。

此时主持人告诉你，你还有一次选择的机会。那么，你会坚持自己之前的决定，还是会选择未打开的另一扇门？

显然，在最初的选择时，能不能选到轿车，符合我们刚才讲到的古典概型，选到轿车的概率为1/3。

主持人为你排除了一个错误答案后，只剩两扇门——一只羊一辆车，不管选哪扇门，获得轿车的概率好像都是1/2，换不换门似乎没什么意义。

那么答案如何呢？如果你坚持己见，不选择换门，你获得轿车的概率仍为1/3；但如果你选择换门，你获得轿车的概率就会上涨到2/3，所以选择换门才是最佳策略。

这个答案听起来很反直觉，是不是？主持人开门排除一只羊后，剩下两扇门不论选择哪个获得轿车的概率都应该是50%才对啊？

别急，让我们从概率论的角度分析一下这个问题。

如下图所示，门后的排列总共有三种基本结果：

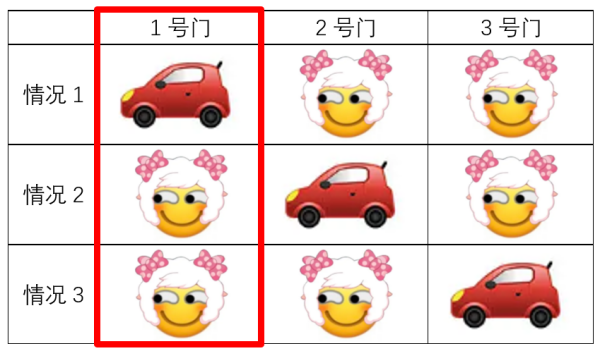
（图片来源：作者自制）

从图中我们可以看到，不管你选择哪个门，你获得轿车的概率都是三分之一。在你选择了一扇门后（假定为1号门），仍有三种情况。这时主持人为你打开了一扇有羊的门，场面上剩下两个门：

（图片来源：作者自制）

还是存在三种等可能的情况：

情况1：轿车在1号门，主持人排除了2或3号门中的任一扇，不换可以得到轿车，换得不到轿车。

情况2：轿车在2号门，主持人排除了3号门后的羊，不换得不到轿车，换可以得到轿车。

情况3：轿车在3号门，主持人排除了2号门后的羊，不换得不到轿车，换可以得到轿车。

因为三个情况的概率仍然相等，所以这个问题仍符合古典概型。由此不难得出，选择不换门，获得轿车的概率为1/3；选择换门，得到轿车的概率为2/3。

为了达到营销的目的，各路商家经常会开展各类抽奖活动，而抽奖活动的规则也五花八门。但实际上，这些令人眼花缭乱的抽奖规则基本上都是对商家有利的，你或许会小赚，但商家永远不亏。

在面对这些繁杂的抽奖活动时，只有了解基本的心理学理论、掌握好概率知识，才不会被黑心商家煽动诱导，不会被繁杂的抽奖规则蒙骗。

最后要强调的是，适度参加抽奖可以成为一种消遣方式，但万万不可沉迷抽奖，更不可过分希望通过抽奖“一夜暴富”，“赌徒心理”不可取！

作者：饭堂科普