最初的光速是如何测量的？

光在空气中的速度为299,552,816 m/s，一般四舍五入为3x10⑻米／秒。这个速度有多快呢？光在一秒钟内前进的距离大约就可以绕地球赤道7圈半，也就是说，几乎一眨眼的时间，光就可以毫不费力的环游世界。从地球到月球的距离约为38万公里，光打个来回也仅仅需要两秒多（事实上，地球和月球之间的准确距离就是计算激光来回所花费时间得到的）。而人类在1969年第一次登月，花费了三天多的时间才到达月球，由此可见光速有多快。光速是目前人类已知速度的上限。既然光速这么快，最初的科学家们是如何测量光速的呢？

▏伽利略的测量

17世纪以前，人们一直认为光是无限快的，甚至连著名科学家开普勒和笛卡尔都对此深信不疑。但一位我们很熟悉的科学家——伽利略，提出了不同的观点。他认为，光速虽然很快，但仍是有限的，并且可以被测量出来。

为了证实自己的猜想，伽利略在1607年设计了历史上第一个光速测量实验。伽利略一行四人，分成A和B两组，分别登上两座相隔1.6千米左右的山峰，每组都携带有一盏改装过的煤油灯。灯的一面加装了滑盖，当放下滑盖时，从另一座山峰上看，亮光就会被挡住。进行实验时，他们只需要快速地拉开滑盖，就能利用煤油灯的光发出信号。除了两盏煤油灯外，他们还携带了钟摆计时器（伽利略发明的计时装置，是摆钟的前身），以及记录数据的纸和笔。

伽利略的实验方法非常简单：A组拉开挡板发出信号的同时开始计时，当B组看到信号后也立即拉开挡板，A组看到B组反馈的光信号后结束计时。伽利略认为，两座山峰间距离的两倍除以计时时间就等于光速。

理论上来讲，伽利略的实验没什么问题，但伽利略没有预料到光速会如此之快——光跨越1.6千米的距离只需要18.75万分之一秒，当时没有任何计时工具可以达到这样的精度，以至于这个实验根本不可能测出光速。如果不计两人的反应时间和遮住灯的时间，光传播这段距离的时间只需要几微秒，以当时的设备条件无法完成测量。伽利略也承认，他没有通过这个实验测出光速，也没有判断出光速是有限的还是无限的。虽然伽利略的实验失败了，但他迈出了人类探索光速的第一步。

▏利用木星测光速

真正意义上的光速测量是从丹麦天文学家奥勒·罗默开始的。1610年，伽利略利用自己改进的望远镜发现了木星的四颗卫星，其中木卫一最靠近木星，每42.5小时绕木星一圈。而且，木卫一的轨道平面非常接近木星绕太阳公转的轨道，所以，有时候木卫一会转到木星背面，太阳的光无法照射到木卫一，地球上的人就看不到这颗卫星了，称为木卫一蚀。

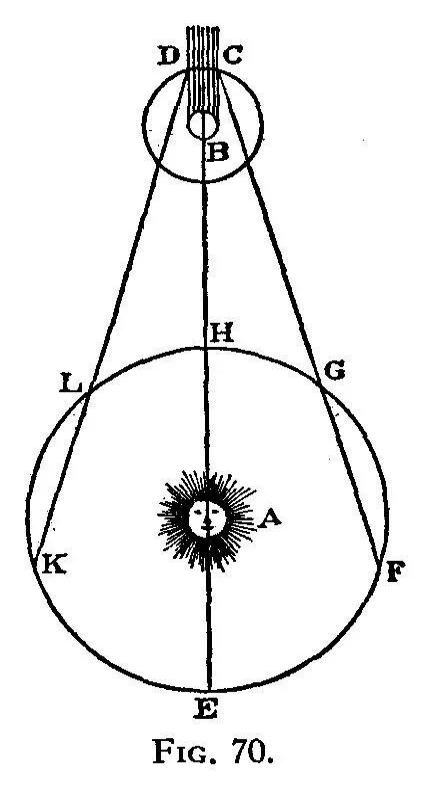
我们来看一个示意图，地球绕着太阳A在圆轨道FGLK上逆时针运动，木卫一绕着木星B也在逆时针运动。木星背后CD之间是木星的阴影区，如果木卫一进入这部分阴影，太阳光照射不到它，人们就无法看到它。也就是说，当木卫一到达C点时就会消失，称为“消踪”，如果木卫一从阴影出来，就能够被人观察到，也就是木卫一到达D点时就会出现，称为“现踪”。罗默就是利用这个现象测量光速的。

首先，我们研究地球靠近木星时发生的消踪和现踪现象。当木卫一到达C点时进入阴影，这个现象的光需要传播一段距离才能到达地球。假设光从C传播到地球时地球位于F点，那么人们观察到消踪现象就比木卫一进入阴影时间晚了一些，这段时间等于CF长度与光速之比。当木卫一到达D点时走出阴影，重新反射太阳光。这个现象也需要一段时间才能到达地球。由于地球在运动，假设这束光到达地球时地球位于G点，那么，人们观察到现踪现象也比木卫一走出阴影时间晚了一些，这段时间等于DG长度与光速之比。

但是，由于CF比DG长，所以消踪现象延迟比现踪现象延迟多一些，即晚发现消踪，早发现现踪。消踪与现踪的时间间隔比木卫一在阴影中的时间要短。我们可以用一个线段图表示这个关系。

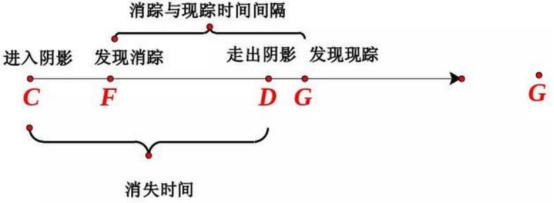
同样，我们可以讨论地球远离木星时的消踪和现踪现象。如果地球到达L发现木星消踪，到达K发现木星现踪，由于地球在远离木星，所以LC的长度小于KD的长度，早发现消踪，晚发现现踪，人们观察到消踪和现踪的时间间隔就会比木卫一实际在木星阴影中的时间长。

1671年到1673年，罗默进行了多次观测，并且得出在地球远离木星时，消踪、现踪时间差比靠近时长了7分钟，并得出了光的速度在214300km/s．这个光速值尽管离光速的准确值相差甚远，但它却是测定光速历史上的第一个记录。牛顿和惠更斯这两位科学巨匠虽然在光到底是粒子还是波的问题上争执不休，但是在光速测量上都支持了罗默的方法。牛顿还测量了光从太阳发射到地球需要8分钟的时间，也就是说：我们看到的太阳是8分钟以前的太阳。

▏接近正确答案

首次准确在地球上，而不是依靠天体运动来测量光速的实验是在1849年由法国物理学家阿曼德·斐索实行的，他使用的方法叫做齿轮测速法。

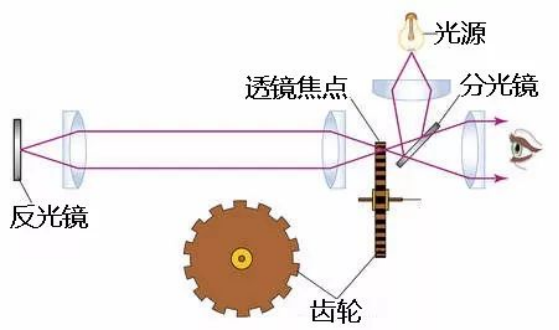
斐索将一个点光源放在透镜的焦点处，在透镜与光源之间放一个齿轮，在透镜的另一测较远处依次放置另一个透镜和一个平面镜，平面镜位于第二个透镜的焦点处。点光源发出的光经过齿轮和透镜后变成平行光，平行光经过第二个透镜后又在平面镜上聚于一点，在平面镜上反射后按原路返回。实验中齿轮的齿与光源齐平，也就是说光线可以通过齿槽，但是如果齿轮的齿在光源前面转动，就会挡住光线。所以，只需转动齿轮，观察光源闪烁。这样，当齿轮转动时，从光源一侧射入镜中的光也在闪烁。

在刚开始转速比较慢的时候，因为光速很快，光仍然会通过同一个齿缝回来。但是当齿轮越转越快，达到某个特定速度时，光返回的时候这个齿缝刚好转过去，于是光就被挡住了，我们就看不到那束光了。当齿轮的转速继续加快，快到一定程度时，光返回的时候恰好可以穿过了下一个齿缝，于是我们又能看见这术光了。这样的话，只要知道齿轮的转速、齿数，还有我们到镜子的距离，就能计算出光速。这个实验最巧妙的地方在于，它不需要用到计时器，之前所有的光速测量实验都失败的根本原因就在于找不到足够精度的计时装置。

就这样，在菲索不懈的努力下，当齿数上升到 720 齿，光源距镜子的距离达 8 千米，转数达到12.67 转/秒的时候，菲索首次观察到光被挡住的现象。当转速继续提高一倍后，菲索又再次看到了光束。由于齿轮的转速已知，即齿轮转动的周期已知。因此，将一转的周期除以总齿数，就可以得到转动一个齿的时间。既然我们知道了光来回到这个距离的时间，再测量观察者到平面镜的距离，我们就可以计算出光速了。

不过这个实验的难点在于光速太快了。因此，他必须设法将平面镜放置得足够远。这个实验的误差因素很多，距离的限制造成的误差影响会比较大。即便如此，斐索测得的光速还是很准确的。经过28次反复实验，他得出的数值约为每秒31.33万公里，与现代准确数值仅相差5%。

▏因测量光速获得诺贝尔奖

200年之后，第一个把光速测量精度大幅提高的人是美国物理学家迈克尔孙。1877到1879年，迈克尔孙改进了傅科发明的旋转镜，示意图如下：

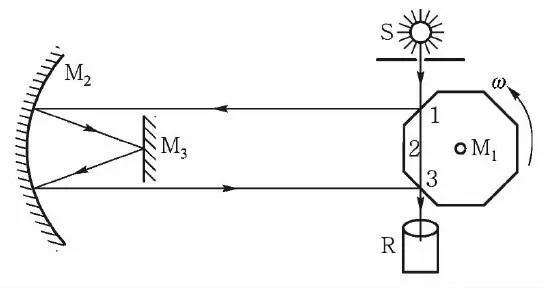
| 迈克尔孙测量光速装置示意图

迈克尔孙在相隔较远的两处分别放置八面镜M1和反射装置M2、M3，让一束光经过八面镜中的镜面1反射后发出，再通过M2和M3反射回八面镜，经过镜面3反射后进入观察目镜。只有在如图所示的位置时，观察目镜处才会有光。如果八面镜转动一点，经过界面1反射的光就无法照射到M2，观察目镜上就看不到光了。

如果让八面镜旋转起来，并且角速度逐渐增大，会发现某个角速度下又可以从观察目镜中看到光了。这是因为界面1刚好倾斜45度角时，光线经过界面1反射到达M2，再返回八面镜时，八面镜刚好转动一格（1/8周期），于是界面2刚好跑到图中镜面3的位置，将光线反射进入观察目镜。由于视觉暂留现象，观察目镜中就好像一直可以看到光。

假设左右两套装置相距为L，当八面镜转动周期为T时，可以从观察镜中看到光，由于L远远大于其它部分的长度，所以光从界面1反射到左侧，再回到八面镜走过的距离近似为：S=2L。根据刚才的分析，光来回运动一次，八面镜刚好走过1格，时间为：t=T/8。因此光的速度为

根据这个原理，迈克尔孙测出光的速度为299853±60km/s，与我们今天测量的更加精确的值非常接近。在当时，这被认为是最精确的数据，而迈克尔逊也因此获得了1907年诺贝尔物理学奖。

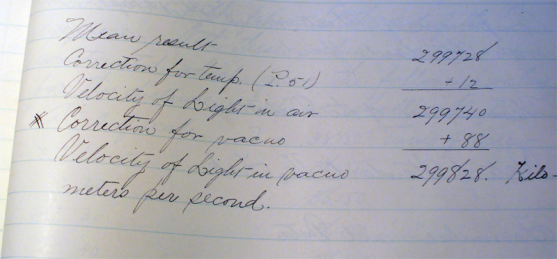
| 迈克尔逊手写的实验结果

这之后几十年里，新的实验技术和实验方法层出不穷，科学家测得的光速值也越来越精确。最终，在1972年，美国标准局埃文森等人用测量激光频率和真空中光的波长的方法，测得光速为299792.458千米/秒。这一数值也在1975年召开的第十五届国际计量大会被作为国际推荐值使用。不久后的1983年，国际计量大会直接规定光速的值为299792458m/s, 并且反过来用光速重新定义了米。也就是说现在的光速值是给定的，不会再改变了，精度也不会再继续提高了，因为它已经成了“米”这个基本单位的基准。所谓的基准，就是指“米”这个单位的最高精度是由光速的值给出的，因为光速值具有很好的稳定性和重复性。人们从无法测量光速到人们测量出较为精确的光速，共经历了300多年的时间。

（图片来源于网络）

作者 | 顾俊哲

计算机科学与技术硕士，毕业后从事网络信息收集与整理工作，关注大众科普知识，探索前沿科技。