寻找现实世界中的“MOSS”（五）：以不变拓扑应万变量子

如果让量子物理学家实现一个心愿，相信有99%的人都会希望在现实世界中构建出一台真正通用化的量子计算机。我们在“寻找现实世界中的‘MOSS’”系列的前4篇中，介绍了量子计算机和量子比特如何实现，在这个系列的最后两篇里，我们将面对量子计算机的“最大bug”。

量子计算机的“最大bug”在于，它虽然性能强大，但其基本运算单元——量子比特，对外界环境的干扰极其敏感，这就导致量子计算机在运算过程中会不可避免地出现错误。那么，我们该怎样弥补这个缺陷呢？

量子计算流程示意图

（图片来源：Veer图库）

量子计算机的软肋——脆弱的量子比特

量子比特抗干扰性差的缺陷，会随着量子计算机运算规模的增大而更加显著。

这是因为量子比特有一种不同于经典计算机比特的奇妙特性，那就是“量子叠加性”。量子比特可以同时处于1态和0态的叠加，也就是说，一个量子比特同时表示两种不同的运算状态。因此，随着量子比特数目N的不断增大，量子计算机的运算能力也将会呈现2^N的指数式爆炸增长。

然而，这种“量子叠加性”十分脆弱，以至于环境中的任何干扰都会破坏量子比特这种奇妙特性，量子比特数目N越大，这种“脆弱”也就越显著。这令无数的量子物理学家和工程师十分头疼。

量子计算概念图

（图片来源：Veer图库）

为了提高量子计算机的运算性能，科学家们需要不断增加量子比特的数量，但数量的增加也会提升量子计算机的运算错误率。就在这进退两难的关头，量子物理学家从数学的“拓扑”概念中找到了解决问题的灵感。

拓扑不变性——“翻花绳”的神秘力量

相信很多小伙伴都听说过数学几何中“拓扑”的概念。它是指一个图形在连续地变换下仍然能保持不变的性质。

不同的几何图片拥有不同的拓扑性质。简单而言，我们可以通过计算几何图形中圆孔的个数，来判断不同几何图形之间的拓扑性质是否相同。

例如，我们生活中常见的茶杯只有把手和杯身所构成的一个圆孔，而我们在超市中购买的甜甜圈也只有中间的一个圆孔。在我们看来，茶杯和甜甜圈完全不是同一种系统状态，然而它们在拓扑结构上都只有一个圆孔（拓扑性质上的连通度都为1）。因此，茶杯可以经过连续的平滑变换成为一个甜甜圈，而保持自身的拓扑性质不变。

拓扑的平滑不变性——从茶杯到握力环

（图片来源：Wikipedia）

因此，具有拓扑不变性的物体并不会由于外界环境的局部干扰，而剧烈地改变自身的拓扑性质。也就是说，我们并不需要刻意关注拓扑系统的局部细微变化，而只需要在意系统整体的拓扑不变性。

不仅如此，我们小时候玩过的翻花绳游戏，也蕴含着奇妙的拓扑不变性。

翻花绳游戏

（图片来源：Veer图库）

如果将一根细绳首尾相连，那么它自身的拓扑结构就天然存在一个圆孔，连通度是1。在翻花绳的行家手中，这根首尾相连的细绳无论经过多么复杂的翻挑操作，无论形成了什么千奇百怪的空间形状，只要一松手，这根细绳又会重新恢复成为一个环形，拓扑性质上的连通度还是1。

换句话说，单纯经过拉伸、折叠等连续平滑的形变，是不会改变某个系统的拓扑性质的，而这种拓扑不变性也是解决量子计算机目前软肋的关键。

拓扑量子计算——拓扑和量子的双向奔赴

既然拓扑性质这么神奇，那么如果量子物理学家可以在现实世界中找到具有拓扑不变性的载体充当量子比特，就可以使量子计算机的拓扑性质保持整体不变，从而保证其不会因外界干扰而产生运算错误，彻底解决量子计算机当前遇到的问题。

实际上，这种大胆的想法并非异想天开。早在1997年，美国物理学家阿列克谢·基塔耶夫 (Alexei Kitaev)就提出了这一设想：把拓扑和量子结合，成为拓扑量子计算。

美国物理学家阿列克谢·基塔耶夫 (Alexei Kitaev)

（图片来源：Wikipedia）

拓扑量子计算作为一种理论上近乎完美的方案，自从1997年被提出以来，就受到无数量子物理学家的广泛关注。

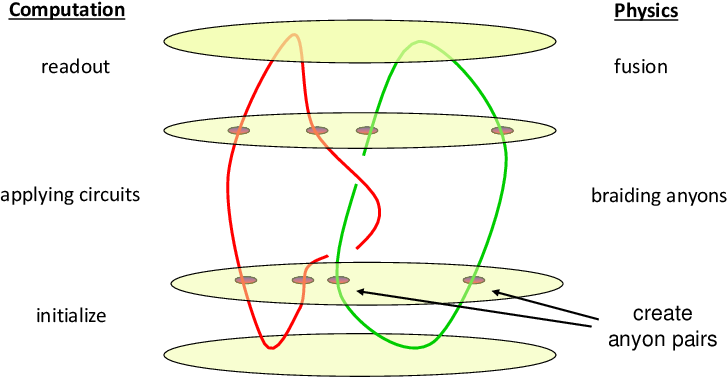
拓扑量子计算的编码与操纵

(图片来源：参考文献[1])

但是我们也不得不思考，现实世界中是否真的存在具有拓扑不变性的物理载体，作为量子比特参与到量子计算中呢？

结语

当奇妙的拓扑遇到神奇的量子，彼此碰撞形成的拓扑量子计算具有更加广阔的应用前景。它可以构建出真正通用的量子计算机，我们将能够突破计算的极限，并且开启处理更加复杂计算任务的大门。这将加速材料设计、药物研发、优化复杂系统等领域的进展，带来前所未有的科学和技术突破。

那究竟如何实现拓扑量子计算呢？我们将在接下来的文章中为大家揭开它的神秘面纱。

参考文献：

[1]Rowell, E.C., & Wang, Z. (2017). Mathematics of Topological Quantum Computing. arXiv: Quantum Algebra.

作者：栾春阳（清华大学物理系）