GPT4技术原理六：范畴的相变与知识的形成

GPT4技术原理六：范畴的相变与知识的形成

“钻石恒久远，一颗永流传”是彻头彻尾的骗局。

科学的角度看，“钻石不是一项好的长期投资！它们正在稳步变成石墨。在常温常压下最稳定的碳形式是石墨。因此，钻石将经历向石墨的相变，尽管需要很长的时间。”

钻石中，碳原子四面体中心的每个碳都与所有四个角的碳相连。石墨中，碳原子以相互滑动层状连接在一起。必须经历重大的结构重组才能从钻石变为石墨——这是有序向无序的转变，反之亦然。

大模型认知框架

类似的转变在大模型中也在不断发生，有序向无序，无序向有序。

《GPT4技术原理五：大模型的幻觉，解铃还须系铃人》中，笔者已经梳理出来如下图所示的大模型认知框架：重整化提取出范畴，持续重整化驱动范畴相变，然后采样做变分推理。

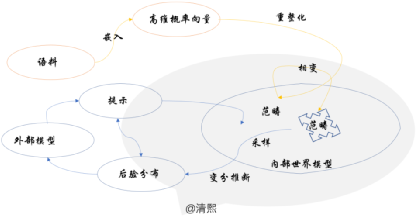
范畴中的相变

本系列较多探讨了重整化与变分推理，却对其中一块关键拼图（范畴的相变）做了留白。重整化如何持续驱动范畴的重构，于不动点附近，促其发生对称性破缺，滑入不同的相空间？

我们知道，范畴的不同的相空间，一如钻石的碳结晶，是大模型从语料中学到的世界模型。

《有感陆奇大模型世界观》中提到：学习的本质是从大量相关信息中提取知识的过程，即人们常说的数据->信息->知识。范畴中的相变机制是什么呢？知识是如何产生的呢？

《万字长文介绍为大语言模型建立的“语言、统计和范畴”数学框架》文中总结过：语言范畴中的对象是语言中的表达式，表达式之间用多头注意力捕捉的概率表征关系，构成概率丰富范畴。

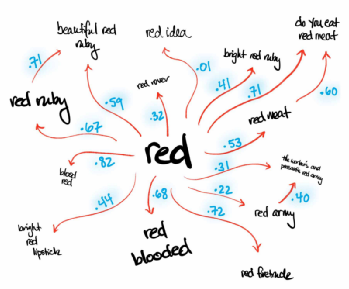
相变的过程

仔细观察这个用概率丰富化了的范畴，由节点和节点之间的边构成，节点与边的概率由重整化群流的学习过程，通过例如Transformer的注意力机制提取。不断训练，不断提取。

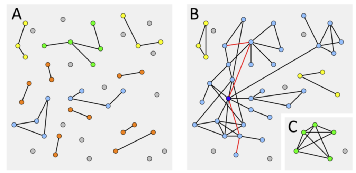
当边的数量少时，范畴中仅有小部件；更多训练，更多的关系被注意力捕捉，生成更多的边，大部件开始出现；持续学习，最终可以将几乎所有节点连结在一起。

重整化群流一层层提取语料中的潜变量和潜变量之间的关系，潜变量形成概率丰富范畴中的节点，而潜变量之间的关系形成该范畴中概率表征的边。这是一个随机的生成过程。

重整化群流生成概率丰富范畴的过程，从上文描述看，特点符合类似 Erdős-Rényi 生成随机图（Random Graph）的随机过程，只不过更加庞大而且复杂。

非同质随机图

数学家是一种把咖啡变成定理的机器。--- Alfred Renyi

从一组n个孤立的顶点开始，在它们之间随机添加连续的边，就可以得到一个随机图。随机图是其中“边随机分布”的图，由匈牙利数学家Paul Erdős和Alfréd Rényi于上世纪50年代末提出。

随机图的思想是，将概率推理和组合数学结合，实践中考虑具有某些固定属性的图的集合，用概率论推导出集合的属性。所以随机图有时也可以泛指在图上的概率分布，由随机过程产生。

通常说的随机图，例如ER(Erdős–Rényi )随机图，是简单同质的，节点具备相同的属性，每条边都是固定的出现概率p。

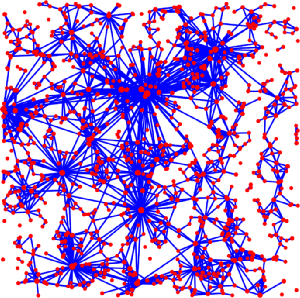
扩展节点类型，用一个n × n矩阵(pij)代替固定的概率p(0≤pij≤1)，可以得到随机图的一个自然推广：对于顶点集[n]，我们写G(n，(pij))，其中i和j由一条概率为pij的边连接，就构成了非同质随机图。

范畴学视角下，大模型学习到的概率丰富范畴，是一张以概率为边、语言表达式为节点，构成的巨大的随机图。因其每个表达式节点类型不同，每条边上的概率也不同，本质上是巨型的非同质随机图。

随机图与相变

ER随机图从一组n个节点开始随机添加边。首先，边会创建小的图形片段，逐渐形成大的组件。随后添加一条边可能会将两个大点的组件连接在一起，因此总连接性会迅速上升。

直到图中的每个节点都通过某种路径连接到其他每个节点。这种总连接性快速上升被称为连接雪崩，代表着一个相变。整个网络性质（例如平均连结路径长度）发生了变化，可以理解为涌现。

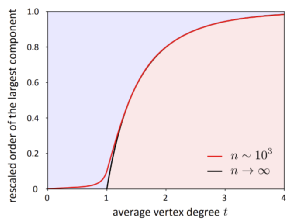
ER随机图中的相变

在连接雪崩之前，连接的节点很少。由于连接的组件很小，因此节点之间的平均路径长度也很小。但随着雪崩期间组件迅速变大，越来越多的节点被连接起来，但它们之间通常只有一条长路径。

随着连接雪崩后添加更多节点，它们有效地提供了捷径，平均路径长度会再次下降。这种路径长度的增加类似于相变期间看到的长程有序，物理上如晶体内质点的有序分布。

随机图是许多复杂系统的基础，严格映射到随机图，证明同构，可以确定系统将发生相变（参考文档2）。同样， 非同质随机图相变也已经被理论上证明 （参考文档 1）。

复杂系统相变

相变具有一般特征，在经典集群模型、人类专业知识和社交网络等多种系统中都能窥见相变的身影。基于信息的度量在检测和分析相变中起到关键作用：

信息熵的不连续性，代表了一阶相变；互信息的峰值意味着二阶相变，费雪几何与转移熵也常被用来做为度量相变的指标。如股票市场的泡沫和崩溃就被证明是互信息峰值处的相变。

大脑神经元网络也已被建模为随机图。神经元之间的连接和相互作用决定了大脑的功能。脑活动实验研究导致一个假设：大脑似乎是在一个临界状态下运作，一个接近相变的状态。

Thomas Kuhn在其著作《科学革命的结构》中讨论到：从哥白尼日心说，到相对论和量子力学，都是人类思维和知识组织的相变。本文阐释了类似的相变一直也在大模型中发生。

至此，恰逢中秋月圆国庆美满，GPT4技术原理系列主体也已经圆满完成。笔者借此篇，祝各位读者中秋家人团圆、国庆幸福康健！

参考资料

1.THE PHASE TRANSITION IN INHOMOGENEOUS RANDOM GRAPHS: https://arxiv.org/pdf/math/0504589.pdf

2.The phase transition in random graphs - a simple proof: https://arxiv.org/abs/1201.6529

3.Warming Up to Enriched Category Theory: https://www.math3ma.com/blog/warming-up-to-enriched-category-theory-part-2

4.Random Graphs: Theory and Applications from Nature to Society to the Brain: https://www.math.tugraz.at/~kang/papers/imn-randomgraphs.pdf

5.Information and phase transitions in socio-economic systems: https://casmodeling.springeropen.com/articles/10.1186/2194-3206-1-9

作者：王庆法 麻省理工学院物理系学者，数据领域专家，首席数据官联盟专家组成员