跨越时空的诡异互动——量子纠缠

量子纠缠正是多粒子的一种量子叠加态。以双粒子为例，一个粒子 A 可以处于某个物理量的叠加态，可以用一个量子比特来表示，同时另一个粒子 B 也可以处于叠加态。当两个粒子发生纠缠，就会形成一个双粒子的叠加态，即纠缠态。如有一种纠缠态就是无论两个粒子相隔多远，只要没有外界干扰，当粒子 A 处于0 态时，粒子 B 一定处于 1 态 ；反之，当粒子 A 处于 1 态时，粒子 B 一定处于 0 态。

再用薛定谔的猫做比喻，就是 A 和 B 两只猫如果形成上面的纠缠态 ：

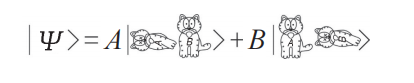
无论两只猫相距多远，即便在宇宙的两端，当猫 A 是“死”的时候，猫 B 必然是“生”；当猫 A 是“生”的时候，猫 B 一定是“死”（当然真实的情况是猫这种宏观物体不可能把量子纠缠维持这么长时间，几万亿分之一秒内就会因“退相干”变成经典状态。但是基本粒子是可以的，如光子）。

2016 年 11 月 30 日，许多来自世界各地的互联网使用者加入了一项有趣的实验 ：贡献自由意志的随机数，用来检验贝尔不等式。时隔一年半，这项实验结果在《自然》（Nature）上正式发表，实验结果再次违反贝尔不等式，又一次验证了量子力学的正确性，即在更吹毛求疵的条件下验证了量子纠缠的存在。

那么什么是贝尔不等式？它为何能够验证量子纠缠？

贝尔不等式这个不等式是由物理学家约翰·贝尔（John Bell）于 1964 年提出的 （见图1）。贝尔假设，如果存在局域隐变量理论，那么按照该理论，测量两个相隔遥远的粒子 A 和粒子 B，它们的间隔除以测量花费的时间大于光速，粒子 A 和粒子 B 之间不会发生任何联系，它们的行为都是事先决定好的，应该符合经典的概率模型。于是贝尔推导出了以下不等式 ：

|h(a, b)-h(a, c)|-h(b, c)≤1

其中，a、b、c 代表测量粒子 A 和粒子 B 的两个探测器的 3 种模式，h(a,b)=(Naa+Nbb-Nab-Nba)/(Naa+Nbb+Nab+Nba) 代表按照局域隐变量理论的测量计数关联的结果（Nab 代表测量 A 的探测器处于模式 a，测量 B 的探测器处于模式 b 时测到的粒子数量，以此类推）。如果存在局域隐变量，必须符合上述不等式，否则如果实验违反上述不等式，那就可以排除局域隐变量理论。

图 1贝尔不等式提出

5 年之后，4 位物理学家 John Clauser、Michael Horne、Abner Shimony 和 R. A. Holt 进一步对贝尔不等式做了推广，提出了更有利于实验验证的 CHSH 不等式 ：

h(a, b)-h(a, b')+h(a', b)+h(a', b' )≤2

现在提到的验证贝尔不等式的实验，主要验证的都是 CHSH 不等式。由于实验技术的限制，直到 1982 年，第一个验证贝尔不等式（CHSH 不等式）的实验才横空出世。得益于激光技术和单光子探测技术的发展（激光和单光子探测器正是归功于量子力学预言和发现），法国物理学家阿斯派克（Alain Aspect）领导的小组利用量子光学方案，在实验上明确地观测到了违反贝尔不等式的结果（测量一系列纠缠光子得到的实验统计结果 >2），随后以蔡林格（A.Zeilinger）小组为代表的世界上很多团队做了一系列实验，都明确地违反了贝尔不等式。于是我们可以说实验已经基本上证实了局域隐变量理论是不对的，量子力学是对的，局域性必须被抛弃。

贝尔不等式检验的实验已经走出实验室，向着更远的距离行进。2016 年 8月，中国成功发射的“墨子号”量子科学实验卫星，在国际上首次在上千千米的星地距离上利用量子纠缠分发检验贝尔不等式，获得了违反贝尔不等式的结果，验证了量子纠缠在跨越 1200 千米的距离上依然存在。

----摘自《大话量子通信》