CPU的工作原理3——如何加减乘除

我们知道CPU的主要功能就是运算，加减乘除运算的基础是加法运算，所以我们先来看如何制作一个加法器。

我们所说的加法器当然是指二进制的加法，请看下图：

左边表格是二个一位二进制数相加的情况分析（二进制没有2，只能通过进位用10描述）。目标有了，怎么实现呢？之前介绍过的异或门的逻辑与此很像（右边的表格），我们看到前三种情况的加法，异或门可以直接实现，而最后一种情况1+1的结果是0而不是10，这里面其实缺少了一个进位，我们可以增加一个与门，解决进位的问题。

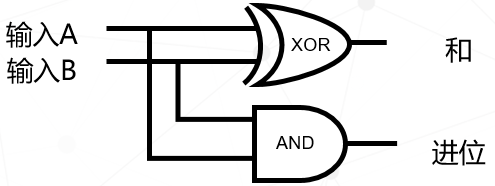
电路图是这样的，其中异或门的输出作为“和的个位数”，与门的输出作为进位。最终实现的结果如下表：

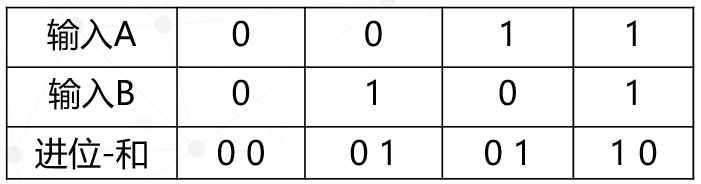
可能有人会想，1+1=10没问题，但0+0=00,0+1=01很是奇怪，能否把前面的0去掉呢？其实我们不用担心，这只是与我们的日常思维习惯有些冲突，并不影响结果的正确性，毕竟在一个数字前面加0和不加0的结果都一样。

这样我们就实现了一位二进制数的加法电路，使用这个符号表示。

为什么叫“半加器”呢？因为还不完善，因为一个完整的加法必然要考虑多位数相加，刚刚分析的只是一位数相加，如果有多位数，必然要考虑前一位数字相加后可能有进位，这个进位也要加进来，所以还可以对这个电路继续完善，直至满足多位数相加，这个完善的加法电路就称为全加器，用这个符号表示。

有了半加器、全加器，就可以实现多位二进制相加了，例如二个八位二进制数相加的电路如下：

可简化为：

减法器的过程稍显复杂，因为减法不考虑进位，但需要考虑借位，而借的这一位如何记录，如何归还都是问题，所以我们要想办法将借位化解掉。我们先从熟悉的十进制减法入手，例如35-16，用借位法很容易得出结果19，但现在我们要避免借位，怎么做呢？我们可以把式子变换一下：

35-16=35-16+100-100=35-16+99+1-100=35+（99-16）+1-100

这样99-16就不涉及到借位，因为对于二位数来说99是最大的。我们继续变换式子：

35+（99-16）+1-100=35+83+1-100=118+1-100=119-100

这时又遇到减法，但是不涉及借位，只需把百位的1去掉即可，结果是19。虽然看起来绕了很大一个弯路，但我们成功地避免了借位。

接下来我们来看二个八位二进制数相减的例子：

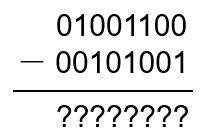
参考前面十进制减法的例子，把这个式子转换为：

这其中涉及到二次减法，其中：

观察一下结果会发现，差和减数是按位取反的，也就是每位0、1正好相反，这个逻辑可以使用如下电路实现：

但问题是，该电路只会对输入取反，而我们要做的是既能做加法也能做减法的电路，所以应该在减法时实现反转，改造电路如下：

当做减法时，取反端=1，才对输入取反，如果是加法，取反端=0，输入不取反。我们将这个电路简化一下，称为求补器：

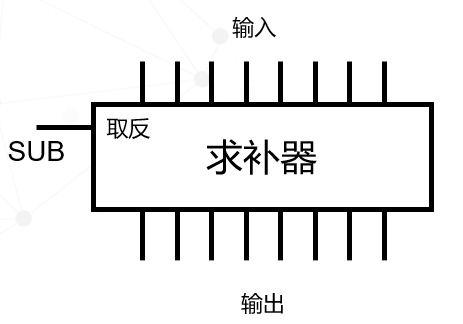
有了求补器，我们就可以将第一个减法变为加上取反后的结果：

这样就只剩下最后一个减法，减去100000000，这个逻辑很简单，只需将首位变为0即可，当然是在做减法的时候。终于我们将所有的减法都化解掉了，现在我们使用加法器，再配合异或门就可以实现加减法运算。

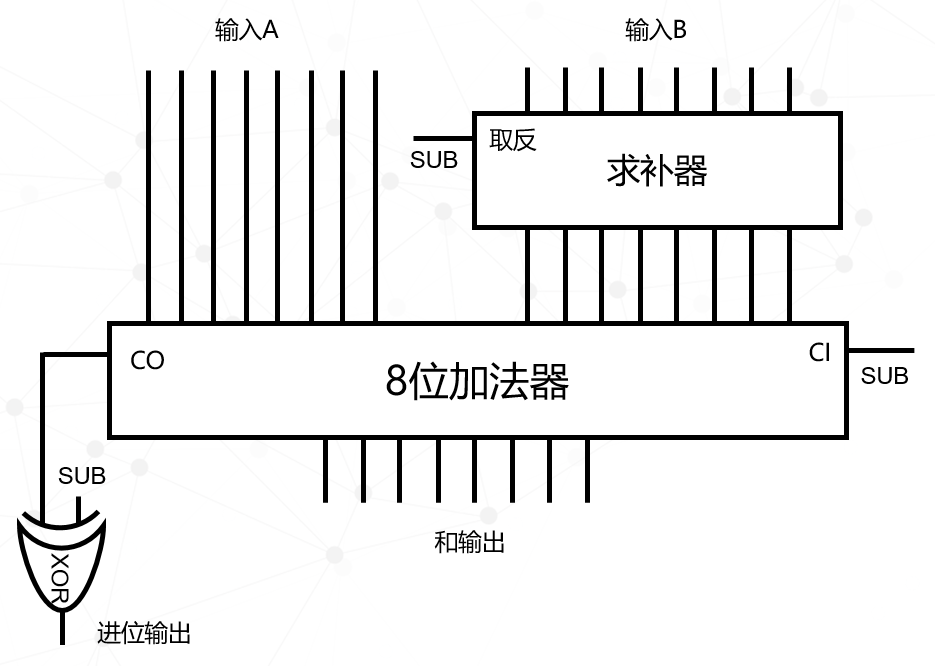
图中有三个SUB端，这就是加减法的切换开关，当SUB=0时，进行加法运算，当SUB=1时，进行减法运算。在减法中，输入B的数据会先通过求补器进行取反，然后再和输入A相加。另外通过加法器的CI（进位输入）可以实现结果+1（因为SUB=1），最后加法器的CO进位输出（也就是结果的首位数据）通过一个异或门处理，减去1，最终得到最后的结果。

至此我们的电路已经能做加减法了，而乘法就是多次加法，除法就是多次减法，所以我们也就能实现乘除的运算了。