复杂网络韧性的边际效应研究 —以配电网重构为例-

“现实生活中，复杂网络随处可见，网络韧性是表征网络抵抗干扰或破坏的能力，韧性研究是复杂网络领域的一个热点，那么复杂网络的韧性提升是否符合边际效应递减规律呢？”

什么是复杂网络

真实系统通过高度抽象得到的具有复杂结构和特性的网络被称为复杂网络。如图1所示，现实生活中各种各样的网络结构可以抽象为复杂网络，如互联网、神经网络、交通运输网、电力网络等。此外，许多常见的社会系统如人际社会关系、学术合作关系等也可以被抽象为复杂网络进行研究和分析。复杂网络与我们的日常生活密切相关，如在信息的传播、流行病的传播和阻断、配电网重构等方面，复杂网络都提供了极有价值的参考模型和分析工具。

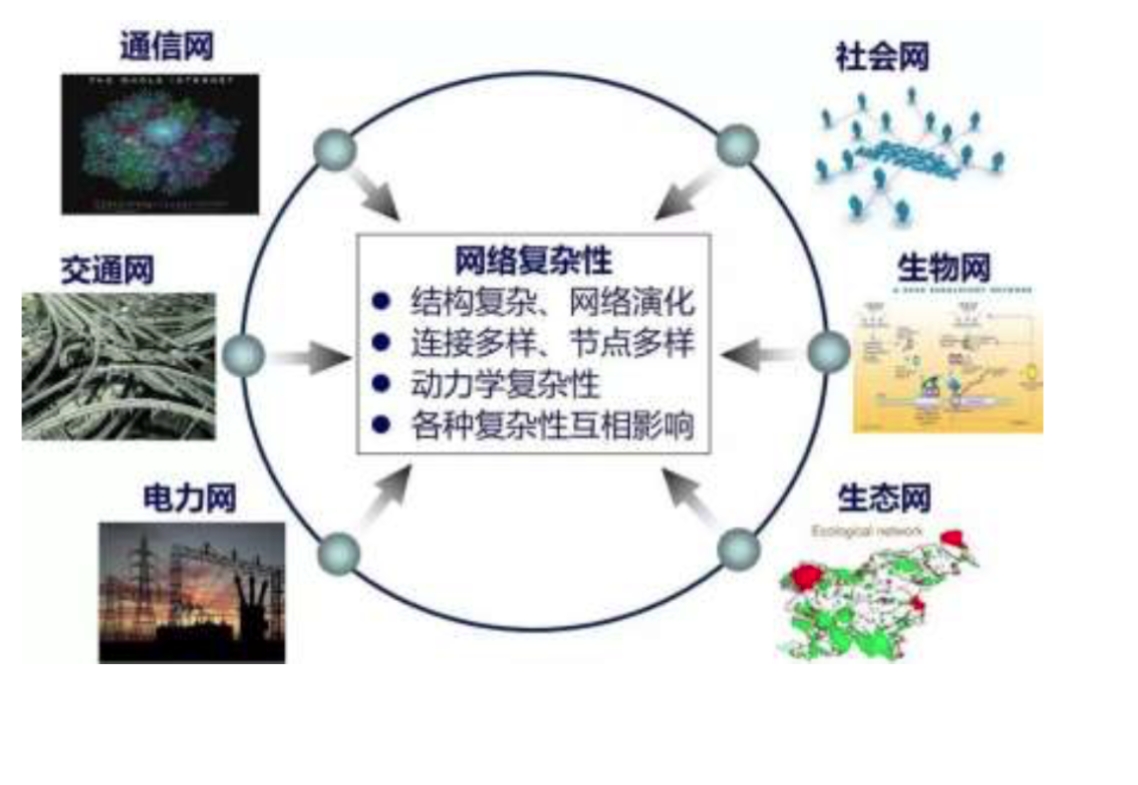
图1 复杂网络示例网络的拓扑性质是指在不考虑节点位置和边具体形态的情况下所表现出来的性质，对应的结构称为网络的拓扑结构。举个例子：- 在人际关系网络中，每个个体抽象为节点，而他们之间的关联关系可以抽象为节点之间的边，如朋友关系、亲戚关系、同事关系等等，这些节点和边的组合构成了一个复杂的人际关系网络，这个网络的拓扑结构可以帮助我们理解人们之间的联系以及信息的流动。

在电力网络中，根据应用场景的不同，节点可以表示母线、变电站、微电网等，而边则表示这些节点之间的连接和传输电力的关系，其拓扑结构可以帮助我们理解电力系统的分布、负载平衡以及电力供应的可靠性，通过分析电力网络的拓扑结构，我们可以优化电力系统的规划和运行方案，从而提高电力供应的质量和效率。其他类型网络对应的拓扑结构也有类似的作用。

因此，网络拓扑研究在理解复杂网络的运作和性质方面起着重要的作用。通过深入理解网络的拓扑结构，我们可以更好地把握现实世界中复杂系统的运作规律，并为设计和优化这些系统提供科学有效的指导。

网络韧性评估指标

由于网络故障的必然性，网络的韧性分析成为一个需要关注的问题。韧性强调的是网络抵御风险能力和故障恢复能力，一个韧性较高的网络可以经受住一定程度的破坏或攻击，而不会完全崩溃或失效。在进行网络韧性分析时，通常关注网络中孤立节点出现的概率，因为这代表网络崩溃或失效。因此，网络对应的径向拓扑结构代表着该网络最脆弱的可能状态（断裂任何一条边将导致网络成为非连通图），该脆弱状态对应的拓扑可由生成树表示。

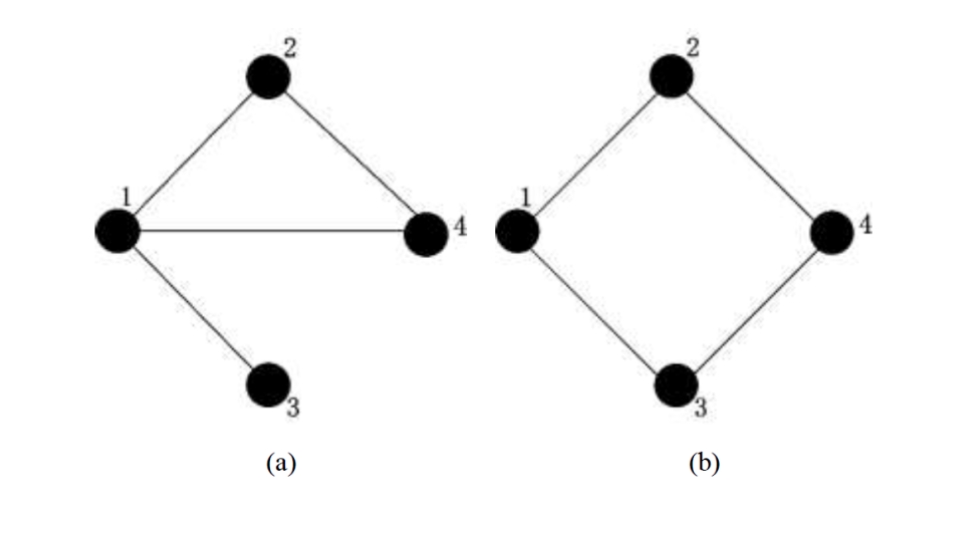
图2 4节点网络说明示例

图2描绘了2种不同的网络拓扑结构，每个网络均由4个节点和4条边组成。图1(a)表示的网络只能生成3棵生成树，一旦边1-3出现故障，网络就会出现失控节点。相比之下，图1(b)代表的系统可以生成4棵生成树，并且在任意一条边出现故障的情况下网络均能保持连通。因此，图1(b)所示网络具有更强的韧性，从而具有更好的生存能力。

根据上述分析，网络的韧性可通过其拓扑所能生成的生成树数量来量化。同时，网络所对应的生成树数量可基于矩阵树定理高效计算：

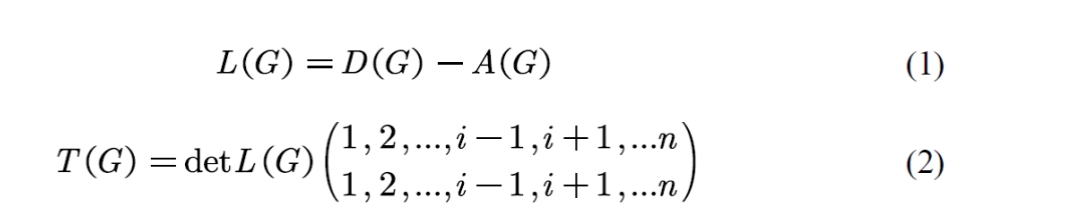
其中，是有n个节点的无向图，式(1)表示计算基尔霍夫矩阵、、分别代表度矩阵及邻接矩阵；式(2)表示图所能生成的生成树数量可通过计算基尔霍夫矩阵的任意n-1阶主子式的行列式值得到。的值越大，网络的韧性越强，反之亦然。

已有学者从复杂网络角度出发提出了多种节点重要性评估指标，包括节点的度、介数中心性、接近中心性、特征向量中心性等，但以上方法都是从节点层面提出的评估指标，存在一定的片面性和局限性，基于生成树数量的网络韧性评估指标则是从网络层面提出的整体性能指标。

网络韧性评估优化

在实际应用中，增加网络连接会带来成本和复杂度增加等问题，因此考虑增加一定数量的网络连接，即考虑在原有网络中增加条边，使得网络韧性最大，构建网络韧性优化模型。
网络韧性优化模型的目标函数为：

网络韧性优化模型的约束条件为：

式(4)表示新增连接关系数量约束，其中和表示节点编号，为0-1决策变量，表示和之间是否需要新建连接关系，表示新增的连接关系数量，为决策者设置的参数，即投资上限。

算例分析

以电力网络为例，选取IEEE 16节点、IEEE 33节点配电网测试算例进行实验。即在给定初始径向拓扑的基础上，添加K条线路，使得网络韧性最大。分别使用启发式策略求解，包括逐步递减策略、最大步长策略、最大步长-度策略、贪婪策略和微调-贪婪策略。

1) 生成树数量变化趋势分析：为了验证可添加线路条数与生成树数量之间的关系，在IEEE 16节点、IEEE 33节点测试算例中，将可添加线路数量K设置为1到10，分别进行10组实验，实验结果如图3所示。在两组实验当中，通过不同策略求解得到的韧性最大的拓扑结构和随机生成的最优拓扑结构（随机生成的韧性最强的网络对应的拓扑），均表现出新增线路数量线性增加时，网络所能形成的生成树数量呈指数增长趋势。

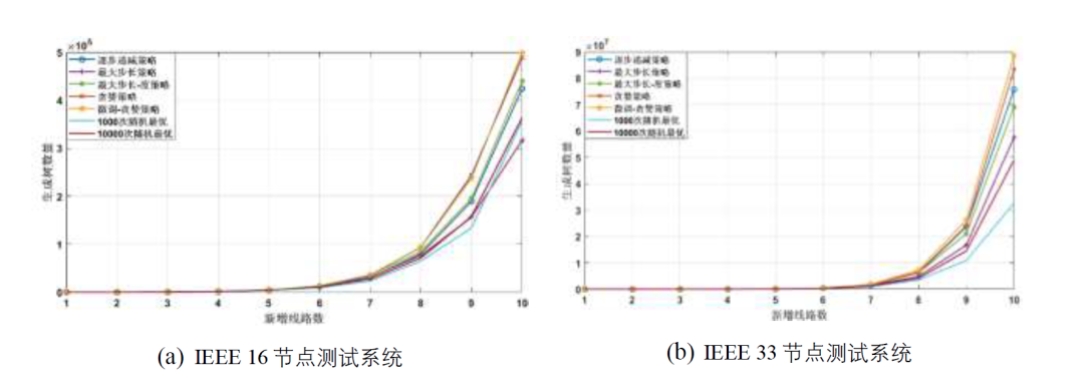
图3 生成树数量变化趋势

2）增长因子分析：增长因子定义为相邻两次计算生成的生成树数量之比，用于定量计算给定拓扑在增加一条线路后带来的网络韧性增长率。图4显示了增长因子在2个测试系统下的变化。随着新增线路数量的增加，增长因子逐渐降低，初期降低速率较快后期变化速率较慢。增长因子下降速度明显减慢的点称之为knee点，表明在该点以后通过添加线路来增强网络韧性的效果不再显著。实验发现对于每个测试系统网络韧性增长率呈现出明显的边际递减效应。

图4显示了增长因子在2个测试系统下的变化

结论

我们围绕复杂网络拓扑优化，定义了基于生成树数量的网络韧性评估指标，并构建了网络韧性的优化模型，不失一般性，以配电网重构为例，研究发现在网络边数量线性递增的情况下，网络韧性评估指标呈现出指数增长的趋势，但增长率表现出明显的边际递减效应，揭示出在以复杂网络为基础的资源优化配置中亟需考虑投资与性能的平衡点，在满足性能需求的前提下，最优化投资。