勾三股四弦五 碧草玉兰修竹——中国古代重要科技发明创造（十六）

图1、图2为《勾股容圆》纪念封。（图片由中国集邮有限公司提供）

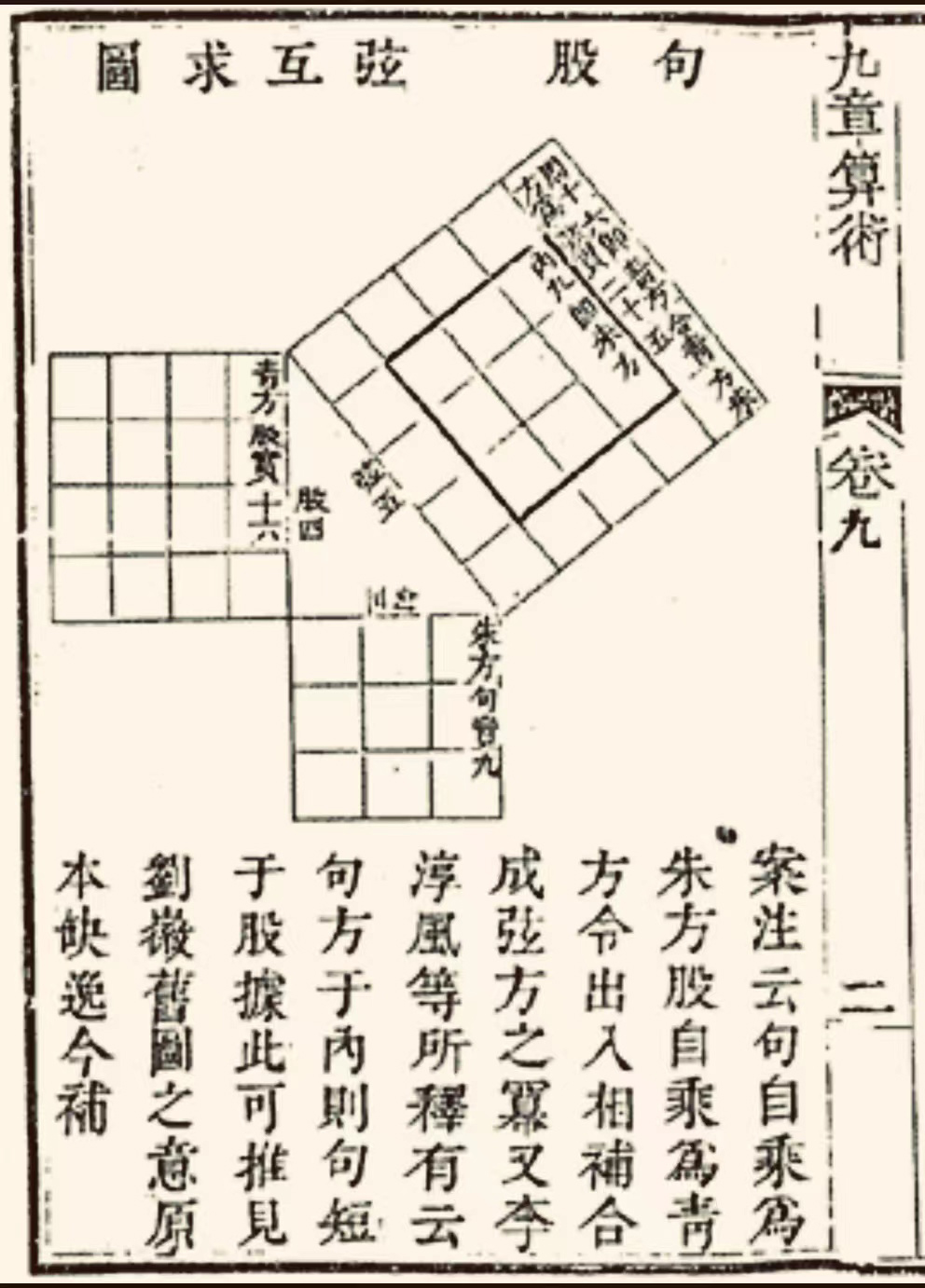
图3、图4、图5、图6分别为《周髀算经》《九章算术》《测圆海镜》《则古昔斋算学》的书影。（图片由作者提供）

据汉代《周髀算经》记载，昔者周公问算于商高，商高对曰：“勾广三，股修四，径隅五。”周公赞曰：“大哉言数。”

古人以“勾三股四弦五”为上联，有对仗下联“六诗七绝八古”者，也有巧对“碧草玉兰修竹”者，又何其美哉言数也！

汉代《九章算术》勾股章第16题“今有勾八步，股十五步。问勾中容圆，径几何？”

该题“术文”为“八步为勾，十五步为股，为之求弦。三位并之为法，以勾乘股，倍之为实。实如法，得径一步。”三位即勾、股、弦，若分别以a、b、c表示，则此圆径d=2ab／a+b+c。

此开勾股容圆问题研究之先河。勾股容圆是通过勾股形（今称直角三角形）和圆的各种相切关系求圆直径的问题，这是中国数学史上的一个重要问题。

魏晋时期的刘徽用出入相补原理和率的理论（借助衰分术）两种方法证明了这个公式。

宋金时期，洞渊在此基础上研究了同一个圆和各种勾股形的相切关系，给出了由勾股形的三边求圆径的9个公式，称为“洞渊九容”。洞渊是道教的派别，通“九数”，活跃于唐宋。

元代李冶由洞渊九容演绎成《测圆海镜》，不仅保留了洞渊九容公式，即9种求直角三角形内切圆直径的方法，而且给出一批新的求圆径公式。

卷一“圆城图式”：“假令有圆城一所，不知周径。四面开门，门外纵横各有十字大道。其西北十字道头，定为乾地；其东北十字道头，定为艮地；其东南十字道头，定巽地；其西南十字道头，定为坤地。所有测望杂法，一一设问如后。”此为《测圆海镜》170问的总题设：今正方形乾坤巽艮容一圆，圆与15个勾股形的各种关系，由此展开。

这是全书的总括图解，由一个直角三角形、它的内切圆以及一些特定的点和直线组成。其中的顶点、圆心和交点都用某个汉字来指代，相当于西方用字母，有异曲同工之妙，是为李冶的创造。

卷一“识别杂记”阐明了圆城图式中各勾股形边长之间的关系以及它们与圆径的关系，共600余条，每条可看作一个定理（或公式），这部分内容是对中国古代关于勾股容圆问题的总结。

后面各卷的习题，都可以在“识别杂记”的基础上以天元术（解方程）为工具推导出来。李冶总结出一套简明实用的天元术程序，并给出化分式方程为整式方程的方法。他发明了负号和一套先进的小数记法，采用了从零到九的完整数码。除零以外的数码古已有之，是筹式的反映。但筹式中遇零空位，没有符号“0”。从现存古算书来看，李冶的《测圆海镜》和秦九韶《数书九章》是较早使用0的两本书，它们成书的时间相差不过一年。《测圆海镜》重在列方程，对方程的解法涉及不多。但书中用天元术导出许多高次方程（最高为6次），给出的根全部准确无误，可见李冶是掌握高次方程数值解法的。

总之，李冶在勾股容圆术中有专门的概念和公式，采用了演绎推理的方法，这在中国数学思想发展史中占有重要的地位。

中国宋元时期，研究测圆术的数学家不在少数。比如朱世杰的《四元玉鉴》中有“勾股测望”门，其中就有这方面的题目。比如有一题是这样的：“今有圆城，不知大小，各中开门。甲、乙俱从城心而出，甲出南门一十五步而立；乙出东门四十步见甲。问城周几何？”

后世学者对《测圆海镜》给予高度的评价。清代阮元认为《测圆海镜》是“中土数学之宝书”；《则古昔斋算学》的作者李善兰称赞它是“中华算书实无有胜于此者”，又补充了3种容圆关系：勾弦上容圆，股弦上容圆，弦外容圆。

（作者王渝生 系国家教育咨询委员会委员，中国科技馆原馆长、研究员）