中科院半导体所论文再登 TNNLS 顶刊，贡献探索数学表达式的新视角

求解数学表达式是机器学习领域中一个非常重要的研究课题，而符号回归 (Symbolic regression,SR) 则是一种从数据中寻找精确数学表达式的方法。

符号回归用于揭示给定观测数据的潜在数学表达式，具有天然的解释和概括能力，能够解释变量之间的因果机制或预测复杂系统的发展趋势，在物理学、天文学等不同领域也有着广泛应用。

一个著名的应用案例是 Kepler 发现行星的轨道，科学家们通过符号回归算法，发现了一些新的天体运动规律，从而推导出它们的运行轨道。这对于人类探索宇宙的星辰大海有着重要贡献。

不过，符号回归研究也有其自身的难点。符号回归侧重于在给定自变量 X 和因变量 Y 的情况下，获得这些元素的最佳组合，并求解最合适的系数。但是，获得最佳组合是一个 NP-hard 问题 (non-deterministic polynomial)，组合空间会随着符号表达式的长度呈指数增长。此外，系数的非线性求解过程和元素组合优化过程是相互干扰的，因此确定精确表达式就非常耗时。

针对这一学术界难题，中国科学院半导体研究所的研究人员将表达式结构的求解视为分类问题，并通过监督学习进行解决，提出一种名为 DeepSymNet 的符号网络来表示符号表达式。与目前流行的几种基于监督学习的 SR 算法相比，DeepSymNet 使用标签 (label) 更短，减少了预测的搜索空间，同时提升了算法鲁棒性。

论文地址：
https://ieeexplore.ieee.org/document/10327762
关注公众号，后台回复「DeepSymNet」即可下载论文

现有方法局限性凸显
目前流行的符号表达结构的解法主要分为两种：

基于搜索的方案

经典的基于搜索的方案有GP (genetic programming ) 算法。首先随机获得许多表达方式作为初始种群，然后通过复制、交换和突变进行进化，并选择优度较小的后代继续进化，直到表达式满足优度要求为止。

另外，在基于搜索的方法中，有一类重要的方法是利用强化学习来搜索合适的表达结构，比如 DSR 算法，它将符号树编码作为序列，并使用深度强化学习中的策略梯度法进行求解。DSR 背后的理念是提高奖励较大的表达式的抽样概率，从而产生误差较小的表达方式。

还有一种用于物理公式的 SR 算法——AIFeynman，主要利用物理学中的先验知识来判断表达式结构，从而将表达式分解为更小的子问题，缩小搜索空间；另一种基于稀疏优化的方法——EQL，主要利用 BP 算法结合稀疏优化来学习参数，从而获得 EQL 网络中的稀疏子网络，进而获得数学表达式结构。

这一类方法除各自缺点明显之外，共同缺点就是速度较慢，因为搜索空间较大，而且无法重复使用求解经验。

基于监督学习的方案

基于监督学习的方案可以克服基于搜索的方案耗时长的缺点，具有代表性的方法有SymbolicGPT、NeSymReS 和 E2E。

* SymbolicGPT 将符号表达式编码为字符串，并将表达式结构解决方案视为语言翻译任务，其语言翻译过程中的 GPT 模型使用大量的人工生成样本进行监督训练；

* NeSymReS 通过前序遍历将符号树编码作为序列，并使用 set Transformer 进行训练；

* E2E 将表达式结构和系数编码成标签进行训练，从而同时预测表达结构和系数。

不过这些方案存在多个等价标签和训练样本不平衡的问题，在训练过程中容易产生歧义，影响算法的鲁棒性。除此外，它们还存在其他缺点，比如 SymbolicGPT 因为用于采样的符号数最多只有四层，所以其考虑的表达式相对简单；E2E 将系数编码为标签，使得标签很长进而影响预测精度等等。

全新解题思路——DeepSymNet
中国科学院半导体研究所的研究人员提出了一种名为DeepSymNet的全新符号网络来表示符号表达式，并展示了DeepSymNet的整体框架，第一层为数据，中间层是隐藏层，最后一层是输出层。

DeepSymNet整体框架

隐藏层节点由运算符号组成，包括+、-、×、÷、sin、cos、exp、log、id 等，其中 id 运算符与 EQL 中的 id 运算符相同。

每个隐藏层中的 id 运算符数等于前一层中的节点数，而其他运算符在每个隐藏层中仅出现一次。运算符 id 与上一层的节点一一对应，其作用使得每一层都能利用上一层的所有信息。其他算子都是普通算子，完全连接到上一层。

id 运算符与上一层之间的连接是固定的，普通运算符与上一层没有连接，或者有一个或两个连接，这意味着在该网络中一个子网络代表一个符号表达式。表达式占用的隐藏层越多，表达式的复杂度就越高，因此，可以用隐藏层的数量来粗略衡量表达式的复杂程度。

但要注意的是，输入层有一个特殊节点「const」，用于表示符号表达式中的常量系数。只有连接到「const」节点的边才有权重（常数系数），以防止符号表达式中出现足够多的常数系数。

总而言之，DeepSymNet 是一个可以表示任何表达式的完整网络，SR 的求解就是在 DeepSymNet 中搜索子网络的过程。

两组实验对照，优势尽显
研究团队分别基于人工生成的数据集和公共数据集进行了测试，并对当前流行的算法进行了比较。

数据集下载地址：
https://github.com/wumin86/DeepSymNet

实验中，DeepSymNet 最多有 6 个隐藏层，最多支持 3 个变量。研究团队为每个标签生成 20 个样本，每个样本包含 20 个数据点。常系数和变量的采样间隔均为 [-2,2]。训练策略是提前停止（即当验证集上的损失不再减少时停止训练）。辅助以 Adam 优化器。

人工生成数据的测试结果

测试结果显示：

* 预测的困难程度会随着预测对象数量的增加而增加，同时表达式的隐藏层（即复杂度）也会增加；

* 标签预测的瓶颈在于操作员的选择；

* DSN2 比 DSN1 更好地求解了最优和近似解；

* 等效标签合并和样本平衡可以增强算法算法的鲁棒性。

首先，DeepSymNet 比符号树能更有效地表示表达式，对于在一个表达式中多次出现的同一模块，DeepSymNet 的平均标签长度比 NeSymRes 短。

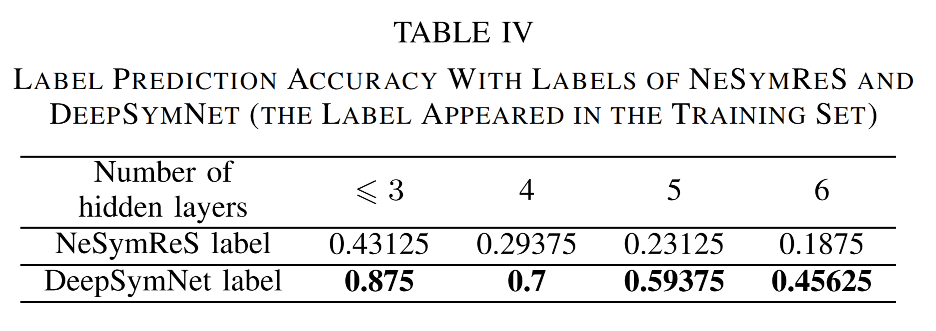
使用 DeepSymNet 标签训练的模型的预测准确率远超使用 NeSymReS 标签训练的模型，如上图所示。这说明 DeepSymNet 标签优于符号树标签。

其次，随着表达式所占隐层数的增加，该模型的预测准确率迅速下降。所以，研究团队提出标签预测可以分为两个子任务——算子预测和连接关系预测，以确保标签预测问题能够得到更好的解决。

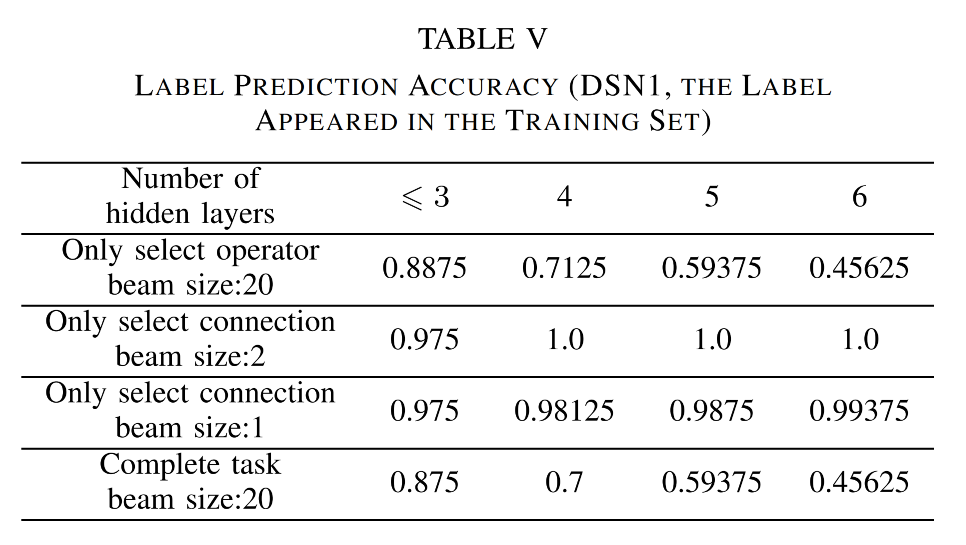
将 DeepSymNet 分为两部分进行训练的结果表明，随着隐层数的增加，算子选择的预测精度急剧下降，而连接关系的预测精度一直很高。这是由于算子选择空间要比连接关系选择空间大的多。所以，为了提高算子选择的准确性，研究人员对算子选择进行了单独训练。

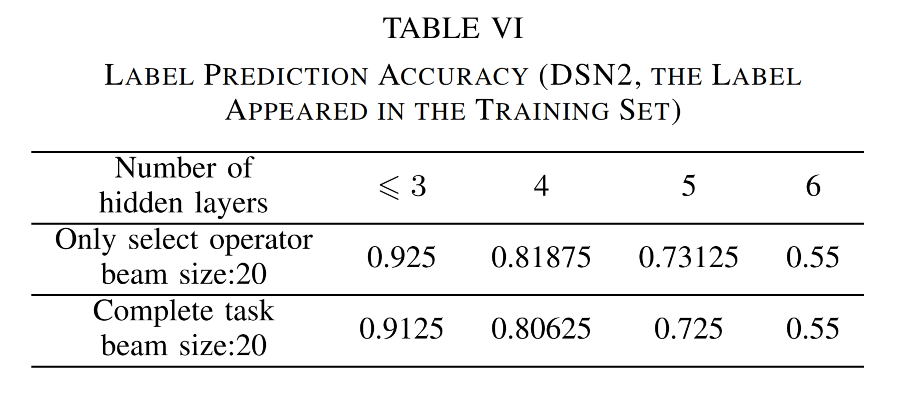
在预测过程中，团队首先使用算子选择模型获得算子选择序列，然后将其输入到训练后的模型 DSN1 中预测连接关系，测试结果如上图。在对运算符选择进行单独训练后，预测精度大大提升。单独训练的模型称为 DSN2。

此外，研究人员还进行了验证等效标签合并和样本平衡增强鲁棒性的消融实验。首先随机抽取了 50 万个训练样本，其中包含 128,455 个不同的标签 (TrainDataOrg)。结果发现这些标签的样本数分布严重不均，最小样本数为 1，最大样本数为 13,196，样本数方差为 13,012.29。

随后团队对样本数进行了平衡，分别获得训练样本 TrainDataB，以及合并等效标签后获得的训练样本 TrainDataBM。

随后基于 3 个训练数据得到模型 DSNOrg、DSNB 和 DSNBM，这 3 个模型在测试集上进行了测试，三者从前至后准确率依次提升，说明增加样本平衡和合并等效标签后，模型求解最优解的准确率得到了提高，确实增强了算法的鲁棒性，提高了算法的性能。

公共数据集测试结果

研究团队使用了 6 个测试数据集：Koza、Korns、Keijzer、Vlad、ODE 和 AIFeynman，从这些数据集中选取了不超过 3 个变量的表达式进行测试。与目前流行的基于监督学习的方法比较显示，该算法 (DSN1、DSN2) 的准确性优于对比算法。

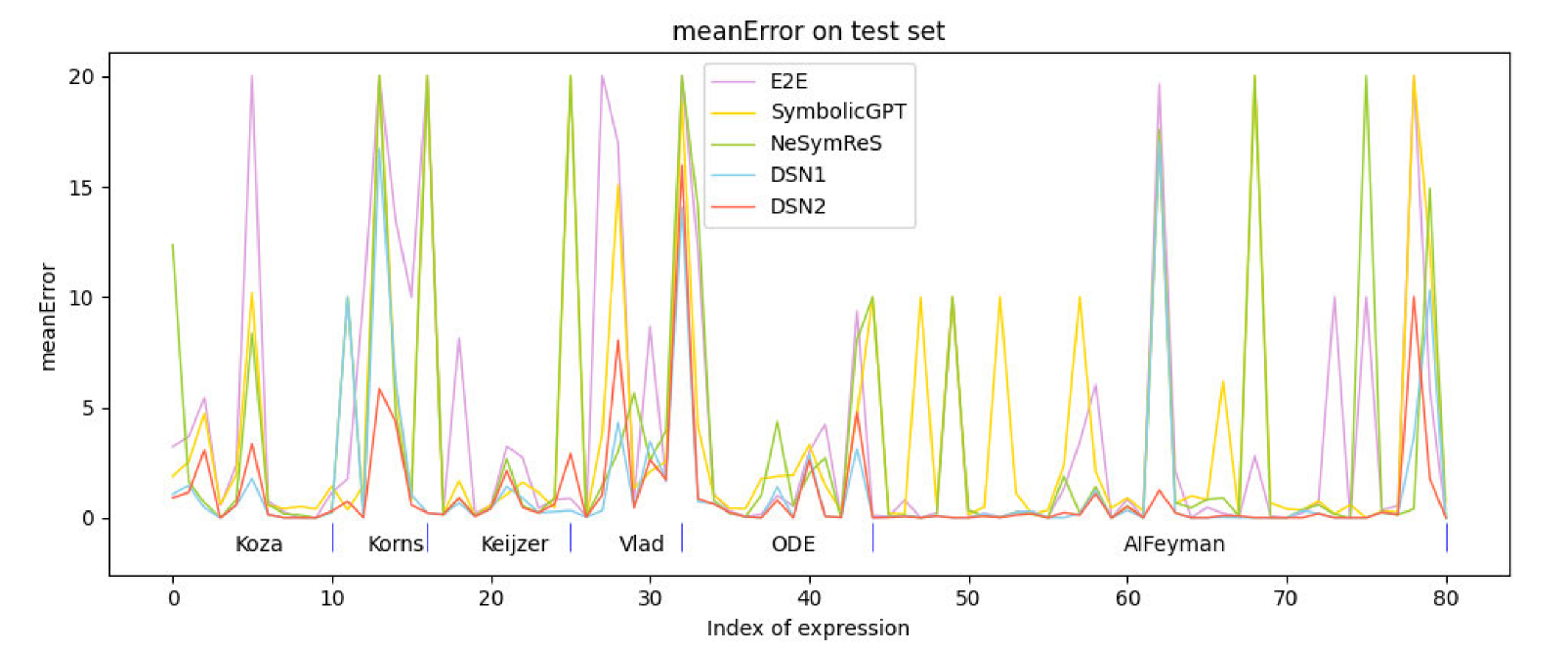
此外，团队将该算法与当前流行的基于搜索的方法 EQL、GP 和 DSR 进行比较，得到结果如下图所示。

该算法 (DSN1、DSN2) 的平均误差最小，得到的表达式的复杂度也最接近真实表达式的复杂度。

综上，根据结果可以得出结论，该团队研究的算法在符号表达式误差、符号表达式复杂度和运行速度 3 个方面都优于对比算法，证实了该算法的有效性。

背后团队星光熠熠
关于符号回归的核心问题，全世界的科学家都在不断努力。尽管在论文中提到，DeepSymNet 仍有一些局限性，但这项研究仍旧为人工智能解决数学问题做出重要贡献，通过将其视为分类问题的方法，无疑为基于监督学习的 SR 方法提供了一个全新的解题思路。

当然，取得这一成就的背后还离不开一群人的热血和汗水，比如论文的第一作者吴敏，从中科院半导体所官网查询，吴敏现为中国科学院半导体研究所助理研究员，参与了「基于深度学习的符号回归及其在半导体器件研发中的应用」、「知识融合的神经网络分治约简符号回归方法」等多个科研项目。

另外，论文作者中的刘婧逸博士，在去年 7 月以第一作者的身份，被人工智能顶刊 Neural Networks 收录了一篇论文，论文题为《SNR: Symbolic Network-based Rectifiable Learning Framework for Symbolic Regression》，为符号回归问题提供了一种具有纠正能力的学习框架。

从相关课题的研究来看，国内正在扎扎实实地引领创新性的方法，未来可期的是，这些理论和研究成果必将在不久的将来对于解决实际问题贡献重要意义。