双曲正弦函数

简介

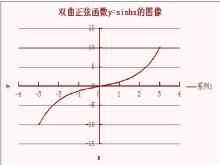应用上常遇到以e为底的指数函数和所产生的双曲函数以及它们的反函数——反双曲函数，而双曲正弦函数是双曲函数的一种，它的定义式1为。

当x的绝对值很大时，双曲正弦函数的图形在第一象限内接近于曲线，在第三象限内接近于曲线。当x=0时，sinhx=sinh0=0。

定义域和值域

双曲正弦函数的定义域为，值域也为。

奇偶性

双曲正弦函数是奇函数，它的图形通过原点且关于原点对称2。

证明如下：

而

根据奇函数的定义，可得出上述结论。

单调性

双曲正弦函数在区间内它是单调增加的。证明如下：

查双曲函数的导数公式，得到：

而双曲余弦函数的值域是。无论取何值，的值永远大于0。可见，双曲正弦函数在内永远是单调递增的。

周期性

无论是双曲正弦函数y=sinhx，还是双曲正切函数y=tanhx、双曲余弦函数y=coshx，它们都不是周期函数。

凹凸性

双曲正弦函数在是凸函数，在是凹函数

证明：根据函数凹凸性的判定定理：设f(x)在[a,b]上连续，在(a,b)内具有一阶和二阶导数，那么：

（1）若在（a,b）内，，则f(x)在[a,b]上的图形是凹的

（2）若在（a,b）内，，则f(x)在[a,b]上的图形是凸的

根据双曲函数的导数公式，求得双曲正弦函数的二阶导数3为：

可见，双曲正弦函数的二阶导数仍然是双曲正弦函数（它本身），而根据双曲正弦函数的单调性，且sinh0=0。可知当x>0时，sinhx的二阶导数大于0。x<0时，sinhx的二阶导数小于0，则可得出上述结论。

导数

双曲正弦函数的导数是双曲余弦函数，即。3

不定积分

双曲正弦函数的积分3是这样的：

其中，大写的C为任意常数。不难发现，除去任意常数C,双曲正弦函数的积分也是双曲余弦函数。

其中，大写的C为任意常数。

泰勒展开式

双曲正弦函数的泰勒展开式3为：

即：

反函数

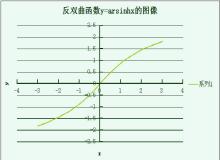双曲正弦函数的反函数是反双曲正弦函数，数学表示上记作arsinh。它的定义式为：

函数y=arsinhx的定义域为，它是奇函数，在区间内单调增加。

其他双曲函数

双曲正弦函数：shx=[e^x-e^(-x)]/24

双曲余弦函数：chx=[e^x+e^(-x)]/24

双曲正切函数：thx=[e^x-e^(-x)]/[e^x+e^(-x)]4

双曲余切函数：chx=[e^x+e^(-x)]/[e^x-e^(-x)]4