共线向量基本定理

定义与证明

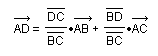如果a≠0，那么向量b与a共线的充要条件是：存在唯一实数λ，使得b=λa。

证明：

（1）充分性：对于向量 a(a≠0)、b，如果有一个实数λ，使 b=λa，那么由实数与向量的积的定义知，向量a与b共线。

定理中的向量a是非零向量，若 a=0，当定理从前往后推出时 ，向量b必为零向量，0与0共线失去讨论意义；当定理从后往前推出时，则向量b为任意向量都可以，同时λ的值不确定，可取任意实数， 即零向量与任意向量共线 ，向量共线的概念已做明确规定 ，故定理中限制向量 a非零。3

（2）必要性***：已知向量a与b共线，a≠0，且向量b的长度是向量a的长度的m倍，即 ∣b∣=m∣a∣。那么当向量a与b同方向时，令 λ=m，有 b=λa*，当向量a与b反方向时，令 λ=-m，有 b=λa。如果b=0，那么λ=0。

（3）唯一性：如果 b=λa=μa，那么 (λ-μ)a=0。但因a≠0，所以 λ=μ。

证毕。1

推论

推论1

两个向量a、b共线的充要条件是：存在不全为零的实数λ、μ，使得 λa+μb=0。

证明：

（1）充分性，不妨设μ≠0，则由 λa+μb=0 得 -b=(λ/μ)a。由 共线向量基本定理 知，向量a与b共线。

（2）必要性，已知向量a与b共线，若a≠0，则由共线向量基本定理知，b=λa，所以 λa-b=0，取 μ=-1≠0，故有 λa+μb=0，实数λ、μ不全为零。若a=0，则取μ=0，取λ为任意一个不为零的实数，即有 λa+μb=0。

证毕。

推论2

两个非零向量a、b共线的充要条件是：存在全不为零的实数λ、μ，使得 λa+μb=0。

证明：

（1）充分性，∵μ≠0，∴由 λa+μb=0 可得 b=(λ/μ)a。由 共线向量基本定理 知，向量a与b共线。

（2）必要性，∵向量a与b共线，且a≠0，则由 共线向量基本定理 知，b=λa；又∵b≠0，∴λ≠0； 取 μ=-1≠0，就有 λa+μb=0，实数λ、μ全不为零。

证毕。

推论3

如果a、b是两个不共线的向量，且存在一对实数λ、μ，使得 λa+μb=0，那么λ=μ=0。

证明：（反证法）

不妨假设μ≠0，则由 推论1 知，向量a、b共线；这与已知向量a、b不共线矛盾，故假设是错的，所以λ=μ=0。

证毕。

推论4

如果三点P、A、B不共线，那么点C在直线AB上的充要条件是：存在唯一实数λ，使得

向量PC=(1-λ)向量PA+λ向量PB。（其中，向量AC=λ向量AB）。

证明：

∵三点P、A、B不共线，∴向量AB≠0，

由 共线向量基本定理 得，

点C在直线AB上 <=> 向量AC 与 向量AB 共线 <=> 存在唯一实数λ，使 向量AC=λ·向量AB

∵三点P、A、B不共线，∴向量PA 与 向量PB 不共线，

∴向量AC=λ·向量AB <=> 向量PC-向量PA=λ·(向量PB-向量PA) <=> 向量PC=(1-λ)向量PA+λ·向量PB。

证毕。

推论5

如果三点P、A、B不共线，那么点C在直线AB上的充要条件是：存在唯一一对实数λ、μ，使得

向量PC=λ向量PA+μ向量PB。（其中，λ+μ=1）

证明：

在推论4 中，令 1-λ=μ ，则λ+μ=1，知：

三点P、A、B不共线 <=> 点C在直线AB上的充要条件是：存在实数λ、μ，使得向量PC=λ向量PA+μ向量PB。（其中，λ+μ=1）

下面证唯一性，若 向量PC=m向量PA+n向量PB，则 m向量PA+n向量PB=λ向量PA+μ向量PB，

即，（m-λ）向量PA+（n-μ）向量PB=0，

∵三点P、A、B不共线，∴向量PA 与 向量PB 不共线，

由 推论3 知，m=λ，n=μ。

证毕。

推论6

如果三点P、A、B不共线，那么点C在直线AB上的充要条件是：存在不全为零的实数λ、μ、ν，使得

λ向量PA+μ向量PB+ν向量PC=0，λ+μ+ν=0。

证明：

（1）充分性，由推论5 知，若三点P、A、B不共线，则 点C在直线AB上 <=> 存在实数λ、μ，使得 向量PC=λ向量PA+μ向量PB（其中，λ+μ=1）。

取ν=-1，则有：λ向量PA+μ向量PB+ν向量PC=0，λ+μ+ν=0，且实数λ、μ、ν不全为零。

（2）必要性，不妨设ν≠0，且有：λ向量PA+μ向量PB+ν向量PC=0，λ+μ+ν=0，则 向量PC=（λ/ν)·向量PA+(μ/ν)·向量PB，（-λ/ν）+（-μ/ν）=1。由推论5 即知，点C在直线AB上。

证毕。

推论7

点P是直线AB外任意一点，那么三不同点A、B、C共线的充要条件是：存在全不为零的实数λ、μ、ν，使得

λ向量PA+μ向量PB+ν向量PC=0，λ+μ+ν=0。

证明：（反证法）

∵点P是直线AB外任意一点，∴向量PA≠**0，向量PB≠0，**向量PC≠0，且 向量PA、向量PB、向量PC两两不共线。

由推论6 知，实数λ、μ、ν不全为零，

（1）假设实数λ、μ、ν中有两个为零，不妨设λ≠0，μ=0，ν=0。则 λ向量PA=0，∴向量PA=0。这与向量PA≠0。

（2）假设实数λ、μ、ν中有一个为零，不妨设λ≠0，μ≠0，ν=0。则 λ向量PA+μ向量PB=0，∴向量PA=（μ/λ）·向量PB，∴向量PA 与 向量PB共线，这与向量PA 与 向量PB不共线矛盾。

证毕。

共线向量定理

定理1

⊿ABC中，点D在直线BC上的充要条件是

其中

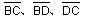都是其对应向量的数量。

证明：有推论5 即可证得。2

定理2

⊿ABC中，点D在直线BC上的充要条件是

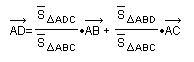其中都是有向面积。通常约定，顶点按逆时针方向排列的三角形面积为正，顶点按顺时针方向排列的三角形面积为负。

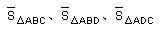
证明：由定理1 即可得证。