拉格朗日乘数法

基本信息

定义介绍

设给定二元函数z=ƒ(x,y)和附加条件φ(x,y)=0，为寻找z=ƒ(x,y)在附加条件下的极值点，先做拉格朗日函数 ，其中λ为参数。

令F(x,y,λ)对x和y和λ的一阶偏导数等于零，即

F'x=ƒ'x(x,y)+λφ'x(x,y)=01

F'y=ƒ'y(x,y)+λφ'y(x,y)=0

F'λ=φ(x,y)=0

由上述方程组解出x,y及λ，如此求得的(x,y)，就是函数z=ƒ(x,y)在附加条件φ(x,y)=0下的可能极值点。

若这样的点只有一个，由实际问题可直接确定此即所求的点。

拉格朗日乘数法是求具有约束条件下多元函数最值问题的有效方法，“只要把拉格朗日函数在区域内部的驻点及函数在区域边界上驻点的函数值加以比较，最大的（最小的）就是函数的最大值（最小值）”。3

几何意义

设给定目标函数为 ，约束条件为 。1

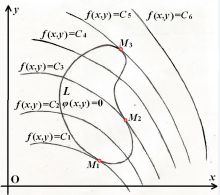如图1所示，曲线 为约束条件 ， 为目标函数的等值线族。

在 、 偏导数都连续的条件下，目标函数 在约束条件 下的可能极值点 ，从几何上看，必是目标函数等值线曲线族中与约束条件曲线能相切的那个切点。

因为两曲线在切点处必有公法线，所以目标函数等值线在点 处法向量 与约束条件曲线在点 处法向量 平行，即

也就是说，存在实数 ，使下式成立

需要注意的是，目标函数等值线与约束条件曲线的切点未必就是目标函数 在约束条件 下的极值点（如图1中的 点）。

证明

以三元函数为例，即求目标函数：u=f(x,y,z) 在限制条件：①G（x,y,z）=0 ② H（x,y,z）=0下的极值。

假定f,G,H具有连续的偏导数，且Jacobi矩阵：1

注释：这里表示的是2x3的矩阵，Hx和Gx分别表示H,G对x求偏导。

在满足约束条件的点处是行满秩，即Rank(J)=2。

先考虑取到条件极值的必要条件，上述约束条件实际是空间曲线的方程。设曲线上一点( , , ) 为条件极值点，由于在该点处rank(J)≠0，不妨假设在( , , )点处 ，则由隐函数存在定理，在点( , ,)附近由该方程可以确定 y=y(x),z=z(x)，其中 =y( ), =z( )，它是这个曲线方程的参数形式。

将它们带入目标函数，原问题就转化为函数：

的无条件极值问题， 是函数 （x）的极值点，因此有 '（x）=0。

也就是

这说明向量2gradf( , , )与向量 正交，即与曲线在点( , , )的切向量正交，因此这点的梯度grad f(,,)可以看做是曲线在点 ( , , ) 处的法平面上的向量。在根据平面上任意一个向量都可以有一对不共线的向量线性表示，又由于这个法平面是由grad G(x0,y0,z0)与gradH( , , )张成的，因此，存在常数a,b使得 gradf( , , )=a*grad G(x0,y0,z0)+b*gradH(x0,y0,z0**)**。

这就是点(,,)为条件极值点的必要条件。

将上述方程写成分量的形式，就可以得到。

求极值

求函数f(x,y,z)在条件φ(x,y,z)=0下的极值。1

方法（步骤）是：

1.做拉格朗日函数L=f(x,y,z)+λφ(x,y,z),λ称拉格朗日乘数；

2.求L分别对x,y,z,λ求偏导，得方程组,求出驻点P(x,y,z)；

如果这个实际问题的最大或最小值存在，一般说来驻点只有一个，于是最值可求。

条件极值问题也可以化为无条件极值求解，但有些条件关系比较复杂，代换和运算很繁，而相对来说“拉格朗日乘数法”不需代换，运算简单一点，这就是优势。

条件φ(x,y,z)一定是个等式，不妨设为φ(x,y,z)=m

则再建一个函数g(x,y,z)=φ(x,y,z)-m

g(x,y,z)=0以g(x,y,z)代替φ(x,y,z)

在许多极值问题中，函数的自变量往往要受到一些条件的限制，比如，要设计一个容积为 V的长方体形开口水箱，确定长、宽和高，使水箱的表面积最小.。设水箱的长、宽、高分别为 x,y,z， 则水箱容积V=xyz。

焊制水箱用去的钢板面积为 S=2xz+2yz+xy

这实际上是求函数 S 在 V 限制下的最小值问题。

这类附有条件限制的极值问题称为条件极值问题，其一般形式是在条件限制下，求函数F的极值。

条件极值与无条件极值的区别

条件