时间膨胀

简介

时间膨胀是一种物理现象：两个完全相同的时钟之中，拿着甲钟的人会发现乙钟比自己的走得慢。这现象常被说为是对方的钟“慢了下来”，但这种描述只会在观测者的参考系上才是正确的。任何本地的时间（也就是位于同一个坐标系上的观测者所测量出的时间）都以同一个速度前进。时间膨胀效应适用于任何解释时间速度变化的过程。 在阿尔伯特·爱因斯坦的相对论中，时间膨胀出现于两种状况：1

• 在狭义相对论中，所有相对于一个惯性系统移动的时钟都会走得较慢，而这一效应已由洛伦兹变换精确地描述出来。
• 在广义相对论中，在引力场中拥有较低势能的时钟都走得较慢。这种引力时间膨胀效应在本条目中只会被略略带过，在主条目中会有更详细的讨论（另见：引力红移）。

狭义相对论中，时间膨胀效应是相互性的：从任一个时钟观测，都是对方的时钟走慢了（当然我们假定两者相互的运动的等速均匀的，两者在观测对方时都没有加速度）。

相反，引力时间膨胀却不是相互性的：塔顶的观测者觉得地面的时钟走慢了，而地面的观测者觉得塔顶的时钟走快了。引力时间膨胀效应对于每个观测者都是一样的，膨胀与引力场的强弱与观察者所处的位置都有关系。

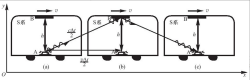
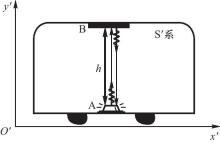在大学物理教学过程中，讲到时间膨胀效应时，通常选用如图1所示的例子。假设有 一个高度为ｈ的火车车厢，相对于地面以速度ｖ水平向右做匀速直线运动，在火车车厢的Ａ点处有一光源竖直向上发出一束光，光束经车顶 Ｂ 处的反射镜反射到Ａ点的接收器。将 Ａ点处发光作为事件1，A点的接收器接收到光作为事件2． 在地面上建立S参照系，在火车上建立S'参照系。在S'系中两个事件的时间间隔是同一地点A测量的,为本征时间 Δt’，且有 Δt'=2hc。图2（a）为A开始发光时，（b）为反射镜刚接收到光并反射时，（ｃ）为Ａ处接收到光时各点的位置示意图。从 Ａ 处发光到 Ｂ 接收到光，再到 Ａ 处接收到光， 两个事件在地面上看是在不同地点测量的．两事件的事件间隔记为 Δt。Δt 为运动时间且满足几何关系 (cΔt/2)2＝ (ｖΔt/2)2+h2。即为时间膨胀效应公式2

定义

狭义相对论中测定时间膨胀的公式为：

当中

是根据某个观测者的时钟，两个本地事件（就是在同地方发生的两个事件）之间的时间间隔——这被称为固有时；

是根据另一个观测者的时钟，同两个事件之间的时间间隔；

v是第二个时钟相对第一个时钟移动的速度；

c是光速；

是洛伦兹因子。

那么移动中的那个时钟走得就比较慢。日常生活中，就算是高速的航天飞行，造成的时间膨胀效应也太小，一般很难被探测到，因此可被忽略。只有在物体达到30,000km/s（光速的1/10）以上时，时间膨胀才显得十分重要。

因为洛伦兹因子而引起的时间膨胀现象是于1897年由Joseph Larmor发现──最起码有电子在原子核运转而引起的现象。

实验证明

时间膨胀的试验已经做过许多次了。自1950年代开始的粒子加速器（如欧洲核子研究组织的加速器）的日常工作，就是持续进行的狭义相对论实验。具体的几个实验包括：

速度时间膨胀实验

• Rossi and Hall（1941）比较了位于山顶和位于海平面的由宇宙射线制造出的μ子数量。尽管μ子从山顶到地面所需的时间已经是几个半衰期，但是在海面的μ子数量却只是少了一点。这是由于μ子相对于测试者以高速运动，导致了可观的时间膨胀效应。经计算，快速移动的μ子的衰变速度比它们相对测试者静止时的衰变速度要慢10倍。

引力时间膨胀实验

• Pound, Rebka在1959年测量出位于较低海拔（所受重力较强）的光波的频率有很小的引力红移。得出的数值和广义相对论预测的数值有小于10%的偏差。不久后Pound和Snider在1964年得出更准的1%偏差，正好就是引力时间膨胀预测的效应。

速度和引力时间膨胀结合实验

• Hafele and Keating在1971年把两个铯原子钟分别放在两架分别向东和西飞的商务客机上，并对比放在美国海军天文台的时钟。飞机上的原子钟应该衰变得更快，因为他们位于距离地面较高，因此引力时间膨胀较小。不过，相反地，它们又会走得较慢，因为他们相对天文台的时钟的速度很快。而当中的引力时间膨胀效应较大，因此两个时钟的时间相对走快了。实验结果和预测的结果相符合。在2005年，英国国家物理实验室公布了他们在另一次相似的实验中所得出的结果。这次实验的飞行时间较1971年的那一次短（来回伦敦和华盛顿），但是实验之中的原子钟更为精确。公布的结果误差为4%。
• 全球定位系统可被视为一项持续进行的狭义和广义相对论实验。轨道上的时钟根据时间膨胀效应被调校成适当的速度，以对应位于地面的时钟。另外，有关广义相对论的一些微调已经编写进定位卫星，要不然，每12个小时定位结果便会有大约7米的偏差。

介子衰期

比较不同速度下μ-介子的衰期是可行的。慢速的介子可在实验室里制造，而快速的介子则在宇宙射线穿入大气层时制造出来。实验室中静止介子的衰期为2.22 μs，由宇宙射线制造出来的介子的速度为光速的98%，衰期为比静止时大5倍左右，和理论相符合。实验中的“时钟”是介子的衰期，而高速运动介子的时钟有着自己的前进速度，也就是比实验室里的“时钟”慢许多。

太空飞行与时间膨胀

根据时间膨胀效应，太空人在相对于地球上的观察者以极高速运动的飞船内时，对于地球观察者而言，尽管地球已经经历了很长的岁月，飞船内的人却没什么老化，因为极大的速度会使飞船（和里面的所有物体）的时间减慢。也就是说，地球上的观察者会发现，当飞船的时钟走了一圈时，地球上的时钟已经转了许多圈了。只要速度够高，这个效应便会明显地显示出来。比方说，对地球上的观察者而言，可能都过了十个钟头了，太空旅行者的手表却只走了一个小时。此效应对飞船或地球这两个坐标系是对称的，因为地球看飞船在动，飞船看地球也在动，而且速度大小相等。也就是说，对太空人而言，地球的时间才是较慢的，可能飞船的时钟过了十分钟，太空人却发现地球上的时钟只过了一分钟(详见更下面的段落以及孪生子佯谬)。

人们更加有可能利用这个效应把人类送到距离地球最近的恒星附近，而不需耗掉航天员的一生光阴(尽管地球上的观察者可能会发现旅行所花的时间仍然大得夸张，但对飞船上的人而言，却只花了更少的一段时间)。然而，要实现这种省时的情况，则需要研发一些更新、更先进的推进技术。另一个问题是，在这么高的速度下，空间里的粒子会折射，成为高能量的宇宙射线。要想飞船不被毁灭，必须用到一些不可思议的防辐射措施。其中一种建议的措施是利用强电磁场把前来的物质离子化，或把它们反弹出去。

目前的航天科技有着许多根本性的限制，如要把飞船加速到接近光速需要大量能量，小型碎片等会对飞船造成威胁。不过，在今天的航天任务中，时间膨胀并不是考虑的因素之一，因为飞船速度相对于光速实在是太小了。另外一个太空飞行会涉及到的时间膨胀效应情况，是接近一个有着极大引力的地方，如黑洞，那里会有强大的引力时间膨胀效应，电影星际穿越中便有相关的桥段出现。

参见

• 四维矢量
• 广义相对论
• 洛伦兹变换
• 闵可夫斯基时空
• 狭义相对论
• 双生子佯谬