三角形中位线定理

定理

三角形的中位线平行于第三边（不与中位线接触），并且等于第三边的一半。

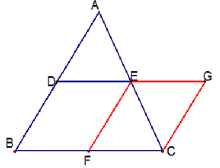
如图1所示，在三角形ABC中，DE是以BC为底的三角形中位线，则可得DE//BC，且DE=BC/2。具体证明过程如下。

证明

如图1，已知△ABC中，D，E分别是AB，AC两边中点。

求证DE平行于BC且等于BC/2

方法一：过C作AB的平行线交DE的延长线于G点。

∵CG∥AD

∴∠A=∠ACG

∵∠AED=∠CEG、AE=CE、∠A=∠ACG（用大括号）

∴△ADE≌△CGE （A.S.A)

∴AD=CG(全等三角形对应边相等)

∵D为AB中点

∴AD=BD

∴BD=CG

又∵BD∥CG

∴BCGD是平行四边形（一组对边平行且相等的四边形是平行四边形）

∴DG∥BC且DG=BC

∴DE=DG/2=BC/2

∴三角形的中位线定理成立.

方法二：相似法：

∵D是AB中点

∴AD：AB=1：2

∵E是AC中点

∴AE：AC=1:2

又∵∠A=∠A

∴△ADE∽△ABC

∴AD：AB=AE：AC=DE：BC=1：2

∠ADE=∠B，∠AED=∠C

∴BC=2DE,BC∥DE

方法三：坐标法：

设三角形三点分别为（x1，y1），（x2，y2），（x3，y3）

则一条边长为 ：根号（x2-x1）^2+(y2-y1）^2

另两边中点为（（x1+x3）/2，（y1+y3）/2），和（(x2+x3）/2，（y2+y3）/2）

这两中点距离为：根号（（x2+x3）/2-(x1+x3）/2）^2+((y2+y3）/2-(y1+y3）/2）^2

最后化简时将x3，y3消掉正好中位线长为其对应边长的一半

方法4：

延长DE到点G，使EG=DE，连接CG

∵点E是AC中点

∴AE=CE

∵AE=CE、∠AED=∠CEG、DE=GE

∴△ADE≌△CGE (S.A.S)

∴AD=CG、∠G=∠ADE

∵D为AB中点

∴AD=BD

∴BD=CG

∵点D在边AB上

∴DB∥CG

∴BCGD是平行四边形

∴DE=DG/2=BC/2

∴三角形的中位线定理成立

方法五：向量DE=DA+AE=(BA+AC)/2=BC/2

∴DE//BC且DE=BC/2

逆定理

逆定理一：

在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线2。

如图2DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。

证明：∵DE∥BC

∴△ADE∽△ABC

∴AD:AB=AE:AC=DE:BC=1:2

∴AD=AB/2，AE=AC/2，即D是AB中点，E是AC中点。

逆定理二：

在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线2。

如图2D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2

证明：取AC中点E'，连接DE'，则有

AD=BD，AE'=CE'

∴DE'是三角形ABC的中位线

∴DE'∥BC

又∵DE∥BC

∴DE和DE'重合（过直线外一点，有且只有一条直线与已知直线平行）

∴E是中点，DE=BC/2

**注意：在三角形内部，经过一边中点，且等于第三边一半的线段不一定是三角形的中位线。**3

如图2，在△ABC中，D是AB中点，E在AC上，DE=BC/2，那么DE不一定是△ABC的中位线。理由如下：

以D为圆心，DE为半径作圆，设⊙D与AC交于另一点E'，则有DE'=DE=BC/2，但DE'不是三角形的中位线。

但在一定条件下该命题是真命题。根据正弦定理解三角形可知，若∠A是锐角，当DE≥AD（即当BC≥AB），或DE=ADsinA（即BC=ABsinA，此时∠C=90°）时，命题成立。若∠A是钝角或直角，则当DE>AD（即BC>AB）时，命题成立。

历史

古巴比伦人（BC1800一 BC1600)在三角形土地的分割实践中，已经知道三角形中位线定理。古希腊数学家欧几里得（公元前3世纪，《几何原本》）则证明了更一般的定理。中国数 、学家刘徽在推导三角形面积公式时（3世纪，《九章算术》注释），实际上也得 出了这个定理，尽管他并未明确提出来。19-20世纪的西方几何教科书中，该定理主要是以更一 般的“平行线分线段成比例”定理或“平行线等分 线段”定理的推论呈现的，是一个并不受特别关 注的“配角”。4