光电效应

定律定义

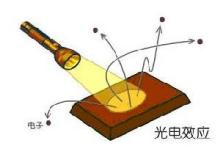
光照射到金属上，引起物质的电性质发生变化。这类光变致电的现象被人们统称为光电效应（Photoelectric effect）。光电效应分为光电子发射、光电导效应和阻挡层光电效应，又称光生伏特效应。前一种现象发生在物体表面，又称外光电效应（photoelectric emission）。后两种现象发生在物体内部，称为内光电效应。

按照粒子说，光是由一份一份不连续的光子组成，当某一光子照射到对光灵敏的物质(如硒)上时，它的能量可以被该物质中的某个电子全部吸收。电子吸收光子的能量后，动能立刻增加;如果动能增大到足以克服原子核对它的引力，就能在十亿分之一秒时间内飞逸出金属表面，成为光电子，形成光电流。单位时间内，入射光子的数量愈大，飞逸出的光电子就愈多，光电流也就愈强，这种由光能变成电能自动放电的现象，就叫光电效应。1

赫兹于1887年发现光电效应，爱因斯坦第一个成功的解释了光电效应（金属表面在光辐照作用下发射电子的效应，发射出来的电子叫做光电子）。光频率大于某一临界值时方能发射电子，即截止频率，对应的光的频率叫做极限频率。临界值取决于金属材料，而发射电子的能量取决于光的波长而与光强度无关，这一点无法用光的波动性解释。还有一点与光的波动性相矛盾，即光电效应的瞬时性，按波动性理论，如果入射光较弱，照射的时间要长一些，金属中的电子才能积累到足够的能量，飞出金属表面。可事实是，只要光的频率高于金属的极限频率，光的亮度无论强弱，电子的产生都几乎是瞬时的，不超过十的负九次方秒。正确的解释是光必定是由与波长有关的严格规定的能量单位(即光子或光量子)所组成。

光电效应里电子的射出方向不是完全定向的，只是大部分都垂直于金属表面射出，与光照方向无关。光是电磁波，但是光是高频震荡的正交电磁场，振幅很小，不会对电子射出方向产生影响。

光电效应说明了光具有粒子性。相对应的，光具有波动性最典型的例子就是光的干涉和衍射。

只要光的频率超过某一极限频率，受光照射的金属表面立即就会逸出光电子，发生光电效应。当在金属外面加一个闭合电路，加上正向电源，这些逸出的光电子全部到达阳极便形成所谓的光电流。在入射光一定时，增大光电管两极的正向电压，提高光电子的动能，光电流会随之增大。但光电流不会无限增大，要受到光电子数量的约束，有一个最大值，这个值就是饱和电流。所以，当入射光强度增大时，根据光子假设，入射光的强度（即单位时间内通过单位垂直面积的光能）决定于单位时间里通过单位垂直面积的光子数，单位时间里通过金属表面的光子数也就增多，于是，光子与金属中的电子碰撞次数也增多，因而单位时间里从金属表面逸出的光电子也增多，电流也随之增大。

研究历史

光电效应首先由德国物理学家海因里希·赫兹于1887年发现，对发展量子理论及提出波粒二象性的设想起到了根本性的作用。菲利普·莱纳德用实验发现了光电效应的重要规律。阿尔伯特·爱因斯坦则提出了正确的理论机制。

十九世纪

1839年，年仅十九岁的亚历山大·贝克勒尔（Alexandre Becquerel），在协助父亲研究将光波照射到电解池（electrolytic cell）所产生的效应时，发现了光生伏特效应。虽然这不是光学效应，但对于揭示物质的电性质与光波之间的密切关系有很大的作用。威勒毕·史密斯（Willoughby Smith）于1873年在进行与水下电缆相关的一项任务，测试硒圆柱高电阻性质时，发现其具有光电导性，即照射光束于硒圆柱会促使其电导增加。

海因里希·赫兹

1887年，德国物理学者海因里希·赫兹做实验观察到光电效应、电磁波的发射与接收。在赫兹的发射器里有一个火花间隙（spark gap），可以借着制造火花来生成与发射电磁波。在接收器里有一个线圈与一个火花间隙，每当线圈侦测到电磁波，火花间隙就会出现火花。由于火花不很明亮，为了更容易观察到火花，他将整个接收器置入一个不透明的盒子内。他注意到最大火花长度因此减小。为了理清原因，他将盒子一部分一部分拆掉，发现位于接收器火花与发射器火花之间的不透明板造成了这屏蔽现象。假若改用玻璃来分隔，也会造成这屏蔽现象，而石英则不会。经过用石英棱镜按照波长将光波分解，仔细分析每个波长的光波所表现出的屏蔽行为，他发现是紫外线造成了光电效应。赫兹将这些实验结果发表于《物理年鉴》，他没有对该效应做进一步的研究。

紫外线入射于火花间隙会帮助产生火花，这个发现立刻引起了物理学者们的好奇心，其中包括威廉·霍尔伐克士（Wilhelm Hallwachs）、奥古斯图·里吉（Augusto Righi）、亚历山大·史托勒托夫（Aleksandr Stoletov）等等。他们进行了一系列关于光波对于带电物体所产生效应的研究调查，特别是紫外线。这些研究调查证实，刚刚清洁干净的锌金属表面，假若带有负电荷，不论数量有多少，当被紫外线照射时，会快速地失去这负电荷；假若电中性的锌金属被紫外线照射，则会很快地变为带有正电荷，而电子会逃逸到金属周围的气体中，假若吹拂强风于金属，则可以大幅度增加带有的正电荷数量。

约翰·艾斯特（Johann elster）和汉斯·盖特尔（Hans Geitel），首先发展出第一个实用的光电真空管，能够用来量度辐照度。艾斯特和盖特尔将其用于研究光波照射到带电物体产生的效应，获得了巨大成果。他们将各种金属依光电效应放电能力从大到小顺序排列：铷、钾、钠钾合金、钠、锂、镁、铊、锌。对于铜、铂、铅、铁、镉、碳、汞，普通光波造成的光电效应很小，无法测量到任何效应。上述金属排列顺序与亚历山德罗·伏打的电化学排列相同，越具正电性的金属给出的光电效应越大。

汤姆孙量度粒子荷质比的光电效应实验装置。

当时研究“赫兹效应”的各种实验还伴随着“光电疲劳”的现象，让研究变得更加复杂。光电疲劳指的是从干净金属表面观察到的光电效应逐渐衰微的现象。根据霍尔伐克士的研究结果，在这现象里，臭氧扮演了很重要的角色。可是，其它因素，例如氧化、湿度、抛光模式等等，都必须纳入考量。

1888至1891年间，史托勒托夫完成了很多关于光电效应的实验与分析。他设计出一套实验装置，特别适合于定量分析光电效应。借助此实验装置，他发现了辐照度与感应光电流的直接比例。另外，史托勒托夫和里吉还共同研究了光电流与气压之间的关系，他们发现气压越低，光电流变越大，直到最优气压为止；低于这最优气压，则气压越低，光电流变越小。

约瑟夫·汤姆孙于1897年4月30日在大不列颠皇家研究院（Royal Institution of Great Britain）的演讲中表示，通过观察在克鲁克斯管里的阴极射线所造成的萤光辐照度，他发现阴极射线在空气中透射的能力远超一般原子尺寸的粒子。因此，他主张阴极射线是由带负电荷的粒子组成，后来称为电子。此后不久，通过观察阴极射线因电场与磁场作用而产生的偏转，他测得了阴极射线粒子的荷质比。1899年，他用紫外线照射锌金属，又测得发射粒子的荷质比为7.3×10emu/g，与先前实验中测得的阴极射线粒子的数值7.8×10emu/g大致符合。他因此正确推断这两种粒子是同一种粒子，即电子。他还测出这粒子所载有的负电荷 。从这两个数据，他成功计算出了电子的质量：大约是氢离子质量的千分之一。电子是当时所知质量最小的粒子。

二十世纪

匈牙利物理学家菲利普·莱纳德

菲利普·莱纳德于1900年发现紫外线会促使气体发生电离作用。由于这效应广泛发生于好几厘米宽区域的空气，并且制造出很多大颗的正离子与小颗的负离子，这现象很自然地被诠释为光电效应发生于在气体中的固体粒子或液体粒子，汤姆孙就是如此诠释这现象。1902年，莱纳德又发布了几个关于光电效应的重要实验结果。第一，借着变化紫外光源与阴极之间的距离，他发现，从阴极发射的光电子数量每单位时间与入射的辐照度成正比。第二，使用不同的物质为阴极材料，可以显示出，每一种物质所发射出的光电子都有其特定的最大动能（最大速度），换句话说，光电子的最大动能于光波的光谱组成有关。第三，借着调整阴极与阳极之间的电压差，他观察到，光电子的最大动能与截止电压成正比，与辐照度无关。

由于光电子的最大速度与辐照度无关，莱纳德认为，光波并没有给予这些电子任何能量，这些电子本来就已拥有这能量，光波扮演的角色好似触发器，一触即发地选择与释出束缚于原子里的电子，这就是莱纳德著名的“触发假说”（triggering hypothesis）。在那时期，学术界广泛接受触发假说为光电效应的机制。可是，这假说遭遇到一些严峻问题，例如，假若电子本来在原子里就已拥有了逃逸束缚与发射之后的动能，那么，将阴极加热应该会给予更大的动能，但是物理学者做实验并没有测量到任何不同结果。

英姿焕发的爱因斯坦在1905年（爱因斯坦奇迹年）发表了六篇划时代的论文。

1905年，爱因斯坦发表论文《关于光的产生和转化的一个试探性观点》，对于光电效应给出另外一种解释。他将光束描述为一群离散的量子，现称为光子，而不是连续性波动。对于马克斯·普朗克先前在研究黑体辐射中所发现的普朗克关系式，爱因斯坦给出另一种诠释：频率为f的光子拥有的能量为E=hf ；其中， h因子是普朗克常数。爱因斯坦认为，组成光束的每一个量子所拥有的能量等于频率乘以普朗克常数。假若光子的频率大于某极限频率，则这光子拥有足够能量来使得一个电子逃逸，造成光电效应。爱因斯坦的论述解释了为什么光电子的能量只与频率有关，而与辐照度无关。虽然光束的辐照度很微弱，只要频率足够高，必会产生一些高能量光子来促使束缚电子逃逸。尽管光束的辐照度很强劲，假若频率低于极限频率，则仍旧无法给出任何高能量光子来促使束缚电子逃逸。

爱因斯坦的论述极具想像力与说服力，但却遭遇到学术界强烈的抗拒，这是因为它与詹姆斯·麦克斯韦所表述，而且经过严格理论检验、通过精密实验证明的光的波动理论相互矛盾，它无法解释光波的折射性与相干性，更一般而言，它与物理系统的能量“无穷可分性假说”相互矛盾。甚至在实验证实爱因斯坦的光电效应方程正确无误之后，强烈抗拒仍旧延续多年。爱因斯坦的发现开启了量子物理的大门，爱因斯坦因为“对理论物理学的成就，特别是光电效应定律的发现让爱因斯坦荣获1921年诺贝尔物理学奖。

图为密立根做光电效应实验得到的最大能量与频率关系线。竖轴是能够阻止最大能量光电子抵达阳极的截止电压，P是逸出功，PD是电势差（potential difference)。

爱因斯坦的论文很快地引起美国物理学者罗伯特·密立根的注意，但他也不赞同爱因斯坦的理论。之后十年，他花费很多时间做实验研究光电效应。他发现，增加阴极的温度，光电子最大能量不会跟着增加。他又证实光电疲劳现象是因氧化作用所产生的杂质造成，假若能够将清洁干净的阴极保存于高真空内，就不会出现这种现象了。1916年，他证实了爱因斯坦的理论正确无误，并且应用光电效应直接计算出普朗克常数。密立根因为“关于基本电荷以及光电效应的工作”获颁1923年诺贝尔物理学奖。

根据波粒二象性，光电效应也可以用波动概念来分析，完全不需用到光子概念。威利斯·兰姆与马兰·斯考立（Marlan Scully）于1969年证明这理论。

数学推导

光束里的光子所拥有的能量与光的频率成正比。假若金属里的自由电子吸收了一个光子的能量，而这能量大于或等于某个与金属相关的能量阈值（称为这种金属的逸出功），则此电子因为拥有了足够的能量，会从金属中逃逸出来，成为光电子；若能量不足，则电子会释出能量，能量重新成为光子离开，电子能量恢复到吸收之前，无法逃逸离开金属。增加光束的辐照度会增加光束里光子的“密度”，在同一段时间内激发更多的电子，但不会使得每一个受激发的电子因吸收更多的光子而获得更多的能量。换言之，光电子的能量与辐照度无关，只与光子的能量、频率有关。

被光束照射到的电子会吸收光子的能量，但是其中机制遵照的是一种非全有即全无的判据，光子所有能量都必须被吸收，用来克服逸出功，否则这能量会被释出。假若电子所吸收的能量能够克服逸出功，并且还有剩余能量，则这剩余能量会成为电子在被发射后的动能。

逸出功 W 是从金属表面发射出一个光电子所需要的最小能量。如果转换到频率的角度来看，光子的频率必须大于金属特征的极限频率，才能给予电子足够的能量克服逸出功。逸出功与极限频率v0之间的关系为

W=h*v0

其中，h是普朗克常数， W是光频率为v0的光子的能量。

克服逸出功之后，光电子的最大动能 Kmax 为

Kmax=hv-W=h（v-v0）

其中，hv 是光频率为 v的光子所带有并且被电子吸收的能量。

实际物理要求动能必须是正值，因此，光频率必须大于或等于极限频率，光电效应才能发生。

光电效应原文

关于光的产生和转化的一个启发性观点

爱因斯坦

1905年3月

在物理学家关于气体或其他有重物体所形成的理论观念同麦克斯韦关于所谓空虚空间中的电磁过程的理论之间，有着深刻的形式上的分歧。这就是，我们认为一个物体的状态是由数目很大但还是有限个数的原子和电子的坐标和速度来完全确定的；与此相反，为了确定一个空间的电磁状态，我们就需要用连续的空间函数，因此，为了完全确定一个空间的电磁状态，就不能认为有限个数的物理量就足够了。按照麦克斯韦的理论，对于一切纯电磁现象因而也对于光来说，应当把能量看作是连续的空间函数，而按照物理学家的看法，一个有重客体的能量，则应当用其中原子和电子所带能量的总和来表示。一个有重物体的能量不可能分成任意多个、任意小的部分，而按照光的麦克斯韦理论（或者更一般地说，按照任何波动理论），从一个点光源发射出来的光束的能量，则是在一个不断增大的体积中连续地分布的。

用连续空间函数来运算的光的波动理论，在描述纯悴的光学现象时，已被证明是十分卓越的，似乎很难用任何别的理论来替换。可是，不应当忘记，光学观测都同时间平均值有关，而不是同瞬时值有关，而且尽管衍射、反射、折射、色散等等理论完全为实验所证实，但仍可以设想，当人们把用连续空间函数进行运算的光的理论应用到光的产生和转化的现象上去时，这个理论会导致和经验相矛盾。

确实在我看来，关于黑体辐射，光致发光、紫外光产生阴极射线，以及其他一些有关光的产生和转化的现象的观察，如果用光的能量在空间中不是连续分布的这种假说来解释．似乎就更好理解。按照这里所设想的假设，从点光源发射出来的光束的能量在传播中不是连续分布在越来越大的空间之中，而是由个数有限的、局限在空间各点的能量子所组成，这些能量子能够运动，但不能再分割，而只能整个地被吸收或产生出来。

下面我将叙述一下我的思考过程，并且援引一些引导我走上这条道路的事实，我希望这里所要说明的观点对一些研究工作者在他们的研究中或许会显得有用。

§1关于“黑体辐射”理论的一个困难

让我们首先仍采用麦克斯韦理论和电子论的观点来考察下述情况。设在一个由完全反射壁围住的空间中，有一定数目的气体分子和电子，它们能够自由地运动，而且当它们彼此很靠近时，相互施以保守力的作用，也就是说，它们能够象气体[分子]运动理论中的气体分子那样相互碰撞。此外，还假设有一定数目的电子被某些力束缚在这空间中一些相距很远的点上，力的方向指向这些点，其大小同电子与各点的距离成正比。当自由的[气体]分子和电子很靠近这些[束缚]电子时，这些电子同自由的分子和电子之间也应当发生保守[力]的相互作用。我们称这些束缚在空间点上的电子为“振子”；它们发射一定周期的电磁波，也吸收同样周期的电磁波。

根据有关光的产生的现代观点，在我们所考察的空间中，按照麦克斯韦理论处于动态平衡情况下的辐射，应当与“黑体辐射”完全等同——至少当我们把一切具有应加以考虑的频率的振子都看作存在时是这样。

我们暂且不考虑振子发射和吸收的辐射，而深入探讨同分子和电子的相互作用（或碰憧）相适应的动态平衡的条件问题。气体[分子]运动理论为动态平衡提出的条件是：一个电子振子的平均动能必须等于一个气体分子平移运动的平均动能。如果我们把电子振子的运动分解为三个相互垂直的[分]振动，那么我们求得这样一个线性[分]振动的能量的平均值为

这里R是绝对气体常数，N是克当量的“实际分子”数，而T是绝对温度。由于振子的动能和势能对于时间的平均值相等，所以能量等于自由单原子气体分子的动能的。如果在21世纪不论由于哪一种原因——在我们的情况下由于辐射过程——使一个振子的能量具有大于或小于的时间平均值，那末，它同自由电子和分子的碰撞将导致气体得到或丧失平均不等于零的能量。因此，在我们所考察的情况中，只有当每一个振子都具有平均能量时，动态平衡才有可能。

我们进一步对振子同空间中存在的辐射之间的相互作用作类似的考虑。普朗克（Planck）先生曾假定辐射可以看作是一种所能想象得到的最无序的过程，在这种假定下，他推导出了这种情况下动态平衡的条件。他找到：

这里是本征频率为ν的一个振子（每一个振动分量）的平均能量，c是光速，ν是频率，而是频率介于ν和之间的那部分辐射在每个单位体积中的能量。

频率为ν的辐射，如果其能量总的说来既不是持续增加，又不是持续减少，那么，下式

必定成立。

作为动态平衡的条件而找到的这个关系，不但不符合经验，而且它还表明，在我们的图象中，根本不可能谈到以太和物质之间有什么确定的能量分布。因为振子的振动数范围选得愈广，空间中辐射能就会变得愈大，而在极限情况下我们得到：

§2．关于普朗克对基本常数的确定

下面我们要指出普朗克先生所作出的对基本常数的确定，这在一定程度上是同他所创立的黑体辐射理论不相关的。

迄今为止，所有经验都能满足的关于的普朗克公式是：

其中，

对于大的值，即对于大的波长和辐射密度，这个公式在极限情况下变成下面的形式：

人们看到，这个公式是同§l 中用麦克斯韦理论和电子论所求得的公式相符的。通过使这两个公式的系数相等，我们得到：

或者

这就是说，一个氢原子重克克。这正好是普朗克先生所求得的数值，它同用其他方法求得的关于这个量的数值令人满意地相符合。

我们因此得出结论：辐射的能量密度和波长愈大，我们所用的理论基础就愈显得适用；但是，对于小的波长的小的辐射密度，我们的理论基础就完全不适用了。

方程

在以爱因斯坦方式量化分析光电效应时使用以下方程：光子能量 = 移出一个电子所需的能量 + 被发射的电子的动能代数形式：其中h是普朗克常数，ν是入射光子的频率，是功函数，从原子键结中移出一个电子所需的最小能量，是被射出的电子的最大动能，ν0是光电效应发生的阈值频率，m是被发射电子的静止质量，vm是被发射电子的速度，注：如果光子的能量（hν）不大于功函数（ϕ），就不会有电子射出。功函数有时又以W标记。这个方程与观察不符时（即没有射出电子或电子动能小于预期），可能是因为某些能量以热能或辐射的形式散失了。

效应

(一)反常光生伏特效应：

光生伏特效应

一般光生电压不会超过Vg=Eg/e,但某些薄膜型半导体被强白光照射会出现比Vg高的多的光生电压，称反常光生伏特效应。（已观察到5000V的光生电压）

70年代又发现光铁电体的反常光生伏特效应（APV）可产生1000V到100000V的电压，且只出现于晶体自发极化方向上，

光生电压：V=(Jc/(σD+△σl))l

(二)贝克勒尔效应：

将两个同样的电极浸在电解液中，其中一个被光照射，则在两电极间产生电位差，称为贝克勒尔效应。

（有可能模仿光合作用制成高效率的太阳能电池）

(三)光子牵引效应：

当一束光子能量不足以引起电子-空穴产生的激光照射在样本上，可在光束方向上于样本两端建立电势差VL，其大小与光功率成正比，称为光子牵引效应。

(四)俄歇效应（1925年法国人俄歇）

用高能光子或电子从原子内层打出电子，同时产生确定能量的电子（俄歇电子），使原子、分子称为高阶离子的现象称为俄歇效应。

应用：俄歇电子能谱仪用于表面分析，可辨别不同分子的“指纹”。

光电效应

(五)光电流效应（1927年潘宁）

放电管两级间有光致电压（电流）变化称为光电流效应。

（1）：低压气体可以放电（约100Pa的惰性气体）

（2）：空间电荷效应与辉光放电：

放电管中由阴极到阳极存在7个不同的区域：

1：阿斯顿暗区：靠近阴极很薄的一层暗区。原因：从阴极由正离子轰击出的二次电子动能很小，不足以激发原子发光。

2：阴极辉区：继阿斯顿暗区后很薄的发光层。

3：阴极暗区：电子从阴极达到该区，获能量越来越大，超过原子电离能，引起大量碰撞电离，雪崩电离过程集中发生在这里。产生电离后电子很快离开，这里形成了很强的正空间电荷，引起电场分布畸变，管压大部分降在此处和阴极间

以上三区为阴极位降区。

4：负辉区：是发光最强的区域。电子在负辉区产生许多激发碰撞发出明亮的辉光。

5：法拉第暗区：电子在负辉区损失能量，进入此区无足够的能量产生激发。

6：正柱区：在此区电子密度与正离子密度相等，净空间电荷为零，因此又称等离子区。

7：阳极区：可看到阳极暗区和阳极辉区。应用：气体放电器件，如气体放电灯（荧光灯、霓虹灯、原子光谱灯、氖泡）、稳压管、冷阴极闸流管等。激光器中用正柱区实现粒子束反转，粒子束装置中冷阴极离子源，半导体工艺中等离子体刻蚀，薄膜溅射沉积，等离子体化学沉积等。

光电流效应机理：亚稳态（寿命约10^(-4)s到10^(-2)s）原子较中性原子易于电离，多产生一些激发原子，尤其是亚稳态原子，可能改变放电管中载流子浓度。

光电流光谱技术应用：光电流光谱无需常规光谱仪的光学系统，从紫外、可见、红外到微波都可产生光电流效应。光电流光谱有8个数量级的动态范围，灵敏度高、噪声小，是一种超灵敏的光谱技术。（1976年格林等用激光证实光电流光谱）

焦希效应：当用可见光连续辐照以空气或绝缘气体为介质的气体电容器时，流经电容器的低频电流将发生变化，称为焦希效应。

马尔特效应：当放电管阴极表面有金属氧化膜，正离子轰击表面时，二次电子发射作用增强，称为马尔特效应。

实验验证

1887年，赫兹在做证实麦克斯韦的电磁理论的火花放电实验时，偶然发现了光电效应。赫兹用两套放电电极做实验，一套产生振荡，发出电磁波；另一套作为接收器。他意外发现，如果接收电磁波的电极受到紫外线的照射，火花放电就变得容易产生。赫兹的论文《紫外线对放电的影响》发表后，引起物理学界广泛的注意，许多物理学家进行了进一步的实验研究。

1888年，德国物理学家霍尔瓦克斯（Wilhelm Hallwachs）证实，这是由于在放电间隙内出现了荷电体的缘故。

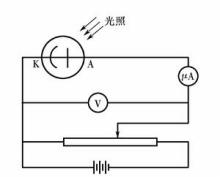1899年，J.J.汤姆孙用巧妙的方法测得产生的光电流的荷质比，获得的值与阴极射线粒子的荷质比相近，这就说明产生的光电流和阴极射线一样是电子流。这样，物理学家就认识到，这一现象的实质是由于光（特别是紫外光）照射到金属表面使金属内部的自由电子获得更大的动能，因而从金属表面逃逸出来的一种现象。1899—1902年，勒纳德（P.Lenard，1862—1947）对光电效应进行了系统的研究，并首先将这一现象称为“光电效应”。为了研究光电子从金属表面逸出时所具有的能量，勒纳德在电极间加一可调节反向电压，直到使光电流截止，从反向电压的截止值，可以推算电子逸出金属表面时的最大速度。他选用不同的金属材料，用不同的光源照射，对反向电压的截止值进行了研究，并总结出了光电效应的一些实验规律。根据动能定理：qU=mv^2/2，可计算出发射出电子的能量。可得出：hf=(1/2)mv^2+I+W

深入的实验发现的规律与经典理论存在诸多矛盾，但许多物理学家还是想在经典电