正态分布

历史发展

正态分布概念是由法国数学家棣莫弗（Abraham de Moivre）于1733年首次提出的，后由德国数学家Gauss率先将其应用于天文学研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。1但德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。这要到20世纪正态小样本理论充分发展起来以后。拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。这是历史上第一次提到所谓“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年，海根（G.Hagen）在一篇论文中正式提出了这个学说。

其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的“元误差” 之和，每只取两值，其概率都是1/2，由此出发，按棣莫弗的中心极限定理，立即就得出误差（近似地）服从正态分布。拉普拉斯所指出的这一点有重大的意义，在于他给误差的正态理论一个更自然合理、更令人信服的解释。因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一（算术平均的优良性，误差的正态性） 为出发点。但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义。

定理

由于一般的正态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x的概率。只要会用它求正态总体在某个特定区间的概率即可。

为了便于描述和应用，常将正态变量作数据转换。将一般正态分布转化成标准正态分布。2

若

服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值。故该变换被称为标准化变换。（标准正态分布表：标准正态分布表中列出了标准正态曲线下从-∞到X（当前值）范围内的面积比例。）

定义

一维正态分布

若随机变量 服从一个位置参数为 、尺度参数为 的概率分布，且其概率密度函数为3

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作 ，读作 服从 ，或 服从正态分布。

μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。

本词条的正态分布是一维正态分布，此外多维正态分布参见“二维正态分布”。

标准正态分布

当 时，正态分布就成为标准正态分布

性质

正态分布的一些性质：3

（1）如果 且a与b是实数，那么 （参见期望值和方差）。

（2）如果 与 是统计独立的正态随机变量，那么：

它们的和也满足正态分布

它们的差也满足正态分布

U与V两者是相互独立的。（要求X与Y的方差相等）。

（3）如果和是独立正态随机变量，那么：

它们的积XY服从概率密度函数为p的分布

其中是修正贝塞尔函数（modified Bessel function）

它们的比符合柯西分布，满足

（4）如果为独立标准正态随机变量，那么服从自由度为n的卡方分布。

分布曲线

图形特征

集中性：正态曲线的高峰位于正中央，即均数所在的位置。

对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。

均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。

曲线与横轴间的面积总等于1，相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。

关于μ对称，并在μ处取最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点，形状呈现中间高两边低，正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线。

参数含义

正态分布有两个参数，即期望（均数）μ和标准差σ，σ2为方差。

正态分布具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N（μ,σ2）。

μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以X=μ为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于μ。

σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。

面积分布

正态函数的不定积分是一个非初等函数，称为误差函数。

实际上误差函数的导数是：

将正态函数换元，误差函数和“正态函数的积分”的关系是：

1、实际工作中，正态曲线下横轴上一定区间的面积（误差函数上下限之差）反映该区间的例数占总例数的百分比，或变量值落在该区间的概率（概率分布）。

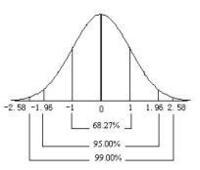
2、正态曲线下，要取到50%概率，横轴半区间长度为0.67448975σ（该值无法用初等方法求解，是由迭代法取得的近似值。）

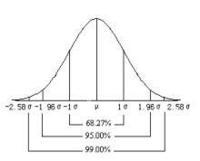
横轴区间（μ-σ,μ+σ）内的面积为68.268949%。

横轴区间（μ-2σ,μ+2σ）内的面积为95.449974%。

横轴区间（μ-3σ,μ+3σ）内的面积为99.730020%。

**“小概率事件”**和假设检验的基本思想： “小概率事件”通常指发生的概率小于5%的事件，认为在一次试验中该事件是几乎不可能发生的。由此可见X落在（μ-3σ,μ+3σ）以外的概率小于千分之三，在实际问题中常认为相应的事件不会发生，基本上可以把区间（μ-3σ,μ+3σ）看作是随机变量X实际可能的取值区间，这称之为正态分布的“3σ”原则。而对于产量更大，试验次数更多的大规模流水线产品，要达到“万无一失”（99.99%）就要取到4σ（99.9936%），而要达到更高的水平，则需要取5σ~6σ长度的半区间，此时误差大约是0.6ppm~0.002ppm，这是工业生产中提出的“六西格玛（6σ）”原则（管理学书籍中提及的六西格玛原则的要求是3.4ppm，这个概率值所对的分布大约在半区间长度4.5σ，这是考虑到系统误差造成的均值偏移μ=1.5σ的情况）。

研究过程

概念及特征：

一、正态分布的概念

由一般分布的频数表资料所绘制的直方图，图⑴可以看出，高峰位于中部，左右两侧大致对称。我们

设想，如果观察例数逐渐增多，组段不断分细，直方图顶端的连线就会逐渐形成一条高峰位于中央（均数所在处），两侧逐渐降低且左右对称，不与横轴相交的光滑曲线图⑶。这条曲线称为频数曲线或频率曲线，近似于数学上的正态分布（normal distribution）。由于频率的总和为100%或1，故该曲线下横轴上的面积为100%或1。

为了应用方便，常对正态分布变量X作变量变换。

该变换使原来的正态分布转化为标准正态分布（standard normal distribution），亦称u分布。u被称为标准正态变量或标准正态离差（standard normal deviate）。

实际工作中，常需要了解正态曲线下横轴上某一区间的面积占总面积的百分数，以便估计该区间的例数占总例数的百分数（频数分布）或观察值落在该区间的概率。正态曲线下一定区间的面积可以通过附表1求得。对于正态或近似正态分布的资料，已知均数和标准差，就可对其频数分布作出概约估计。

查附表1应注意：①表中曲线下面积为-∞到u的左侧累计面积；②当已知μ、σ和X时先按式u=（X-μ）/σ求得u值，再查表，当μ、σ未知且样本含量n足够大时，可用样本均数X1和标准差S分别代替μ和σ，按u=（X-X1）/S式求得u值，再查表；③曲线下对称于0的区间面积相等，如区间（-∞，-1.96）与区间（1.96，∞）的面积相等，④曲线下横轴上的总面积为100%或1。

图2 正态曲线与标准正态曲线的面积分布

正态分布的应用某些医学现象，如同质群体的身高、红细胞数、血红蛋白量、胆固醇等，以及实验中的随机误差，呈现为正态或近似正态分布；有些资料虽为偏态分布，但经数据变换后可成为正态或近似正态分布，故可按正态分布规律处理。

一般正态分布与标准正态分布的区别与联系

正态分布也叫常态分布，是连续随机变量概率分布的一种，自然界、人类社会、心理和教育中大量现象均按正态形式分布，例如能力的高低，学生成绩的好坏等都属于正态分布。它随随机变量的平均数、标准差的大小与单位不同而有不同的分布形态。标准正态分布是正态分布的一种，其平均数和标准差都是固定的，平均数为0，标准差为1。

曲线应用

综述

1、估计频数分布 一个服从正态分布的变量只要知道其均数与标准差就可根据公式即可估计任意取值范围内频数比例。4

2、制定参考值范围

（1）正态分布法 适用于服从正态（或近似正态）分布指标以及可以通过转换后服从正态分布的指标。

（2）百分位数法 常用于偏态分布的指标。表3-1中两种方法的单双侧界值都应熟练掌握。

3、质量控制：为了控制实验中的测量（或实验）误差，常以 作为上、下警戒值，以 作为上、下控制值。这样做的依据是：正常情况下测量（或实验）误差服从正态分布。

/4、正态分布是许多统计方法的理论基础。检验、方差分析、相关和回归分析等多种统计方法均要求分析的指标服从正态分布。许多统计方法虽然不要求分析指标服从正态分布，但相应的统计量在大样本时近似正态分布，因而大样本时这些统计推断方法也是以正态分布为理论基础的。

频数分布

例1.10 某地1993年抽样调查了100名18岁男大学生身高（cm），其均数=172.70cm，标准差s=4.01cm，①估计该地18岁男大学生身高在168cm以下者占该地18岁男大学生总数的百分数；②分别求X+-1s、X+-1.96s、X+-2.58s范围内18岁男大学生占该地18岁男大学生总数的实际百分数，并与理论百分数比较。

本例，μ、σ未知但样本含量n较大，按式（3.1）用样本均数X和标准差S分别代替μ和σ，求得u值，u=（168-172.70）/4.01=-1.17。查附表标准正态曲线下的面积，在表的左侧找到-1.1，表的上方找到0.07，两者相交处为0.1210=12.10%。该地18岁男大学生身高在168cm以下者，约占总数12.10%。其它计算结果见表3。

表3 100名18岁男大学生身高的实际分布与理论分布

|| ||

综合素质研究

教育统计学统计规律表明，学生的智力水平，包括学习能力，实际动手能力等呈正态分布。因而正常的考试成绩分布应基本服从正态分布。考试分析要求绘制出学生成绩分布的直方图，以“中间高、两头低”来衡量成绩符合正态分布的程度。其评价标准认为：考生成绩分布情况直方图，基本呈正态曲线状，属于好，如果略呈正（负）态状，属于中等，如果呈严重偏态或无规律，就是差的。

从概率统计规律看，“正常的考试成绩分布应基本服从正态分布”是正确的。但是必须考虑人与物的本质不同，以及教育的有所作为可以使“随机”受到干预，用曲线或直方图的形状来评价考试成绩就有失偏颇。许多教育专家（如上海顾泠沅、美国布鲁姆等）已经通过实践论证，教育是可以大有作为的，可以做到大多数学生及格，而且多数学生可以得高分，考试成绩曲线是偏正态分布的。但是长期受到“中间高、两头低”标准的影响，限制了教师的作为，抑制了多数学生能够学好的信心。这是很大的误会。通常正态曲线有一条对称轴。当某个分数（或分数段）的考生人数最多时，对应曲线的最高点，是曲线的顶点。该分数值在横轴上的对应点与顶点连接的线段就是该正态曲线的对称轴。考生人数最多的值是峰值。