中国科大在非晶固体振动特性的研究中取得新进展

与结构有序的晶体不同，非晶固体中原子的空间排列混乱无序，导致非晶固体的本征振动模式与晶体中的声子有显著差异。德拜模型成功描述了晶体在低温下的热力学性质，该模型指出，晶体的低频声子态密度D(ω)与频率满足标度律：D(ω)∼ωd-1，其中d为空间维度，并由此可以获得晶体比热c与温度T的正确关系：c∼Td。作为非晶固体的代表，玻璃的低温比热不满足上述关系，这暗示着玻璃的低频本征振动态密度并不简单遵循德拜标度律。玻璃的结构无序导致低频区出现大量非声子的本征振动模式，这些模式的态密度满足怎样的标度关系是理解玻璃反常低温热属性的关键，也是近年来研究和争论的热点。

近日，中国科大物理学院、合肥微尺度物质科学国家研究中心的徐宁教授研究组与中国科大物理学院的童华教授及安徽大学物理与光电工程学院的王利近教授合作，给出了非晶固体低频本征振动态密度的新图像，相关成果以“Low-frequency vibrational density of states of ordinary and ultra-stable glasses”为题2024年2月16日在线发表于《自然•通讯》（Nature Communications）。

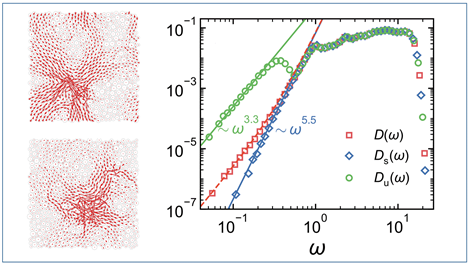
图1.二维不稳定（左上图）和稳定（左下图）非晶固体的最低频本征振动模式及相对应的本征振动模式态密度（右图）。其中Ds(ω)、Du(ω)和D(ω)分别为稳定固体、不稳定固体以及它们加权平均的态密度。

该研究创新性地将非晶固体依照对边界形变的稳定性分为稳定和不稳定两类，发现这两类非晶固体在低频非声子本征振动模式的态密度上展现出两种指数截然不同但鲁棒的标度律，如图1所示。不稳定非晶固体的标度指数与空间维度无关，均约为3.3，该指数与2017年徐宁教授及合作者发表于《物理评论快报》（Physical Review Letters, 2017, 119: 215502）的文章所预言的指数吻合，从而给出了该指数的物理解释。稳定非晶固体的标度指数则展现出了对空间维度的依赖，约为d+3.5，该指数形成的物理机制目前尚不清楚，但是其鲁棒性为理论研究提出了新的问题，也可以用来检验相关理论。以往的研究发现，非晶固体低频本征振动态密度的标度指数对一些参数有依赖性，而该研究表明，这种参数依赖是稳定和不稳定非晶固体加权平均的结果，从而解决了关于非晶固体低频本征振动态密度标度指数的争议，给出了统一的物理图像，深化了对非晶固体低频振动特性的理解。

玻璃研究历史上存在著名的Kauzmann佯谬，形成玻璃的过冷液体的熵随温度的降低有很快的下降，如果这种趋势一直延续，在未达到零温之前过冷液体的熵就会低于晶体的熵。这种趋势显然是不合理的，因为这将最终违反热力学第三定律。为了解决这一矛盾，理论预言存在一个Kauzmann温度，在这个温度，过冷液体将形成与晶体熵一致的理想玻璃。该研究进一步揭示了超稳定玻璃在接近理想玻璃状态时低频本征振动特性的演化，发现非声子模式的数目随着温度的降低而下降，并有可能在某温度处完全消失。基于该趋势，理想玻璃的低频本征振动将可能由类声子模式主导，虽然结构无序，但却和晶体有相似的本征振动行为，从而给出了理想玻璃可能的物理特性，同时也为设计具有类晶体性质的非晶材料提供了新思路。