经济博弈论之鲁宾斯坦讨价还价模型

经济博弈论之鲁宾斯坦讨价还价模型

讨价还价是市场经济中最常见的事情，也是一种典型的消耗战。今天我们将通过鲁宾斯坦讨价还价模型来具体分析消耗战的一般特点。讨价还价模型(Bargain Model)是1982年，阿里尔·鲁宾斯坦 （Ariel Rubinstein）用完全信息动态博弈的方法，对基本的、无限期的完全信息讨价还价过程进行了模拟，并据此建立了完全信息轮流出价讨价还价模型，也称为鲁宾斯坦模型。

模型假设

甲乙两人分一块蛋糕（总体为1），甲乙轮流做出决策。首先由甲给出一个分割方案，乙可以选择接受还是拒绝；如果乙拒绝甲的方案，则由乙来重新给出另一个方案，让甲选择接受还是拒绝。如此循环直至其中一个人选择接受对方的方案为止，博弈宣告结束。同时二人的贴现率相同，贴现因子都是δ。

1.三阶段讨价还价

首先为了简化模型先进行一个三阶段的讨价还价，也就是说到第三阶段的时候乙要接受甲的方案。此博弈的策略式如下图所示。

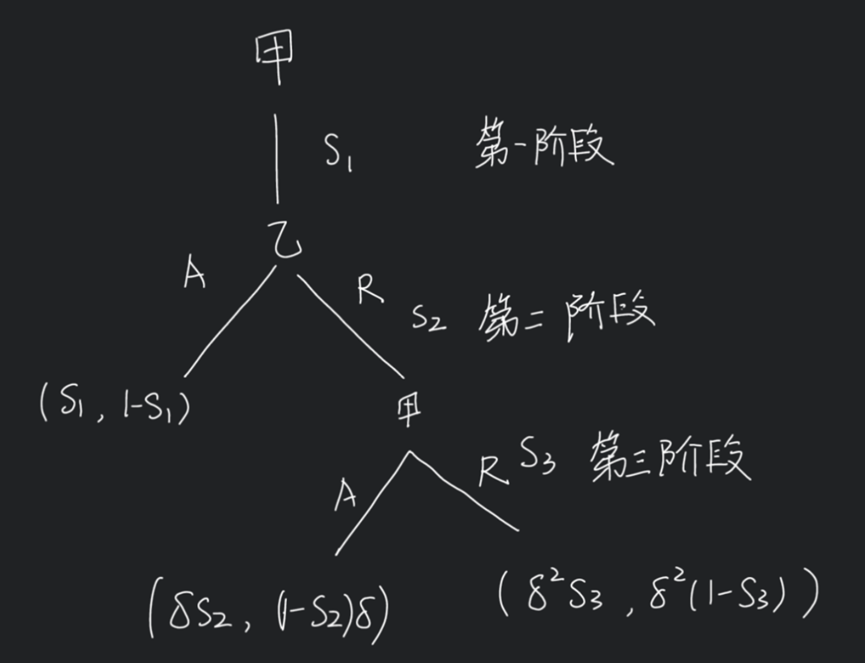
第一阶段，甲提出方案自己获得s1，乙获得1-s1。如果乙选择结束则博弈结束，双方收益为（s1,1-s1）；如果乙选择拒绝则进行下一阶段。

第二阶段，乙提出方案，甲获得s2，乙获得1-s2。如果甲接受，博弈结束，双方收益为

（δs2，（1-s2）δ）；如果甲选择拒绝则进行下一阶段。注：不要忘记贴现因子！

第三阶段，甲提出方案自己获得s3，乙获得1-s3。因为只有三个阶段所以在这个时候乙必须选择接受，所以双方的收益为（δ2s3，（1-s3）δ2）。

求均衡，采用逆向归纳法。

III. 在第三阶段的时候，因为甲知道这个时候乙一定要选择接受，所以甲会选择全要即s3=1。

II. 在第二阶段的时候，乙为了防止甲在这个时候拒绝就要使分配的收益不低于第三阶段的收益，让甲接受的收益≥甲拒绝的收益。为了方便计算则按照=来计算。故δs2=δ2即s2=δ。

I.在第一阶段的时候，同理，必须满足让乙接受的收益≥乙拒绝的收益。故1-s1=（1-s2）δ

将s2=δ代入其中可得s1=1-δ+δ2。所以此时双方收益为（1-δ+δ2，δ-δ2）。

此时双方收益相减的话会得到（1-δ）2+δ2＞0，因此这时候甲的收益大，而对于乙来说也是一个相对的最优解。

2.四阶段讨价还价

三阶段的时候是甲最后提出方案，而四阶段则是乙提出方案，这次又有什么不同呢？让我们来一起探究一下吧。

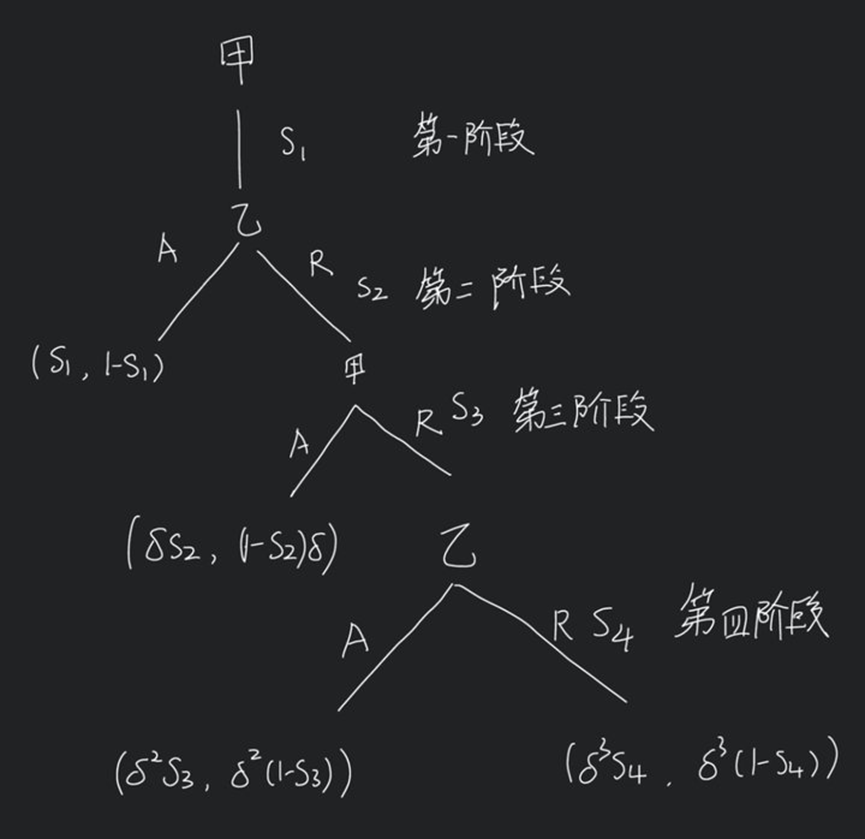
接着第三阶段再往下推一个阶段如上图所示。各阶段的分析也和第三阶段基本相同，直接来看结果吧。

IV. 第四阶段的时候，乙提出方案。s4=0，双方收益为（0，δ3）.

III. 第三阶段的时候，甲提出方案。（1-s3）δ2=（1-s4）δ3即s3=1-δ

II. 第二阶段的时候，乙提出方案。 S2δ=δ2（1-δ）即s2=δ（1-δ）

I.第一阶段的时候，甲提出方案。1-s1=（1-s2）δ即s1=1-δ+δ2-δ3。双方的收益此时为（1-δ+δ2-δ3，δ-δ2+δ3）。

甲的收益-乙的收益的时候，借助一些计算软件可以得出当贴现因子不同时甲乙收益也在不断变化。这种结果反应了乙在不断地跟甲耗时间，虽然甲最终可以获得全部的收益，但是随着时间的拉长，也会给甲带来一些损失。损失越大耐心越小，甲愿意分给乙的收益也越多。

而无限期的讨价还价，还有贴现因子的不同时，均衡的结果则要求参与者要有足够的耐心，在行动之前等待足够长的时间。

图源百度（讨价还价模型实例）

这种结果和现象在现实生活中还存在很多例如利润分配、商品交易谈判等。所以这个模型还是具有比较强烈的实际意义的。而讨价还价在现实中采取的策略一般为投石问路、报价策略、抬价压价、价格让步、最后报价等。总之学会鲁宾斯坦讨价还价模型对于以后生活中还是有很大的帮助的。