焊接结构在众多工程领域中都有着大量的应用[1],在服役过程中会受到复杂的循环载荷作用,长此以往易发生疲劳破坏。据统计90%的焊接结构破坏都是由焊接接头的疲劳失效造成的[2],某些焊接接头疲劳失效甚至会带来灾难性的后果,正如上世纪美国的Silver Bridge坍塌事件,Silver Bridge是一座钢结构桥梁,位于西弗吉尼亚州欢乐点(Point Pleasant)与俄亥俄州加利波利斯(Gallipolis)之间,由于两条疲劳裂纹未能及时地被发现,大桥于1967年12月倒塌,倒塌后的大桥如图1所示,整个倒塌过程不足20 s,造成46人死亡的重大事故[3]。

图1 Silver Bridge坍塌[3]
为保证设备的安全运行,人们一直在努力寻找能准确预测焊接结构疲劳寿命和疲劳强度的方法,同时对焊接缺陷、焊接残余应力、焊趾区的几何外形对焊接结构疲劳寿命产生的影响进行了研究,也发展了焊接结构的延寿技术。本文介绍了焊接结构疲劳寿命的预测方法、影响焊接结构疲劳寿命的因素和延寿技术的研究现状和进展。
1. 疲劳评定方法
根据焊接接头周围的应力分布,可将其分为3个区,分别是名义应力区、结构应力区、缺口应力区,如图2所示,由此发展出3种焊接结构的疲劳评定方法:名义应力法、热点应力法、局部法[4−5]。
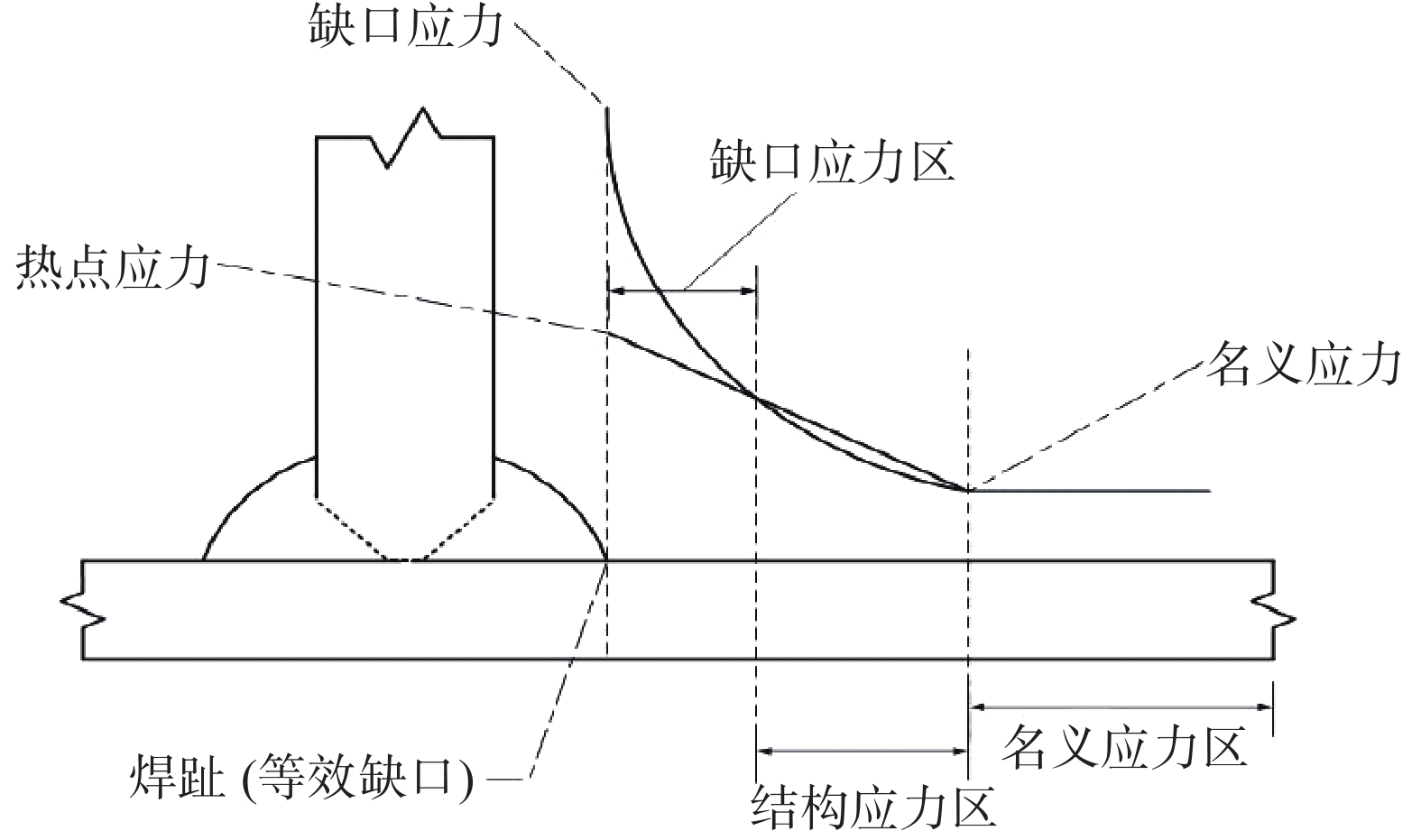
图2 焊接接头附近的应力分布
1.1 名义应力法
名义应力法是假定焊接结构的疲劳寿命由材料的疲劳寿命决定,结合焊接接头的名义应力和应力集中系数得到一个当量应力,再根据材料的应力–寿命(S–N)曲线得到相应的寿命。名义应力法注重对焊接结构寿命的预测和疲劳强度的设计[6],若有多级载荷,则需结合损伤积累理论[3]。
该方法以名义应力为疲劳评估参量,依据不同的接头形状和其加载方式把焊接接头分为质量不同的多个类型,再通过大量的疲劳试验建立起对应的S–N曲线,在评价焊接接头疲劳寿命的时候依据实际情况选取相应质量等级的S–N曲线。但正因为名义应力法的S–N曲线和结构的接头形状、载荷类型、几何形式等因素紧密相关,导致很多复杂焊接结构不能找到与之适配的S–N曲线,使得疲劳强度预测变得十分繁琐,这便是名义应力法的不足之处。但对于一些简单焊接接头的疲劳评定还是比较便捷有效的。
1.2 热点应力法
热点应力也叫结构应力,是国际焊接协会推荐的评定焊接结构疲劳寿命的一种方法,是指危险截面上危险点的应力。热点是裂纹起源的部位,应力集中较为严重,在疲劳载荷的作用下应力集中最严重处会发热[7],故称之为热点疲劳。热点疲劳大多发生在焊趾处,因焊趾处存在缺口效应,故焊趾处的应力又叫缺口应力σln。缺口应力的组成如式(1)和(2)所示,结构应力在焊趾处达到最大,即为热点应力。焊趾处的应力分布如图3所示。
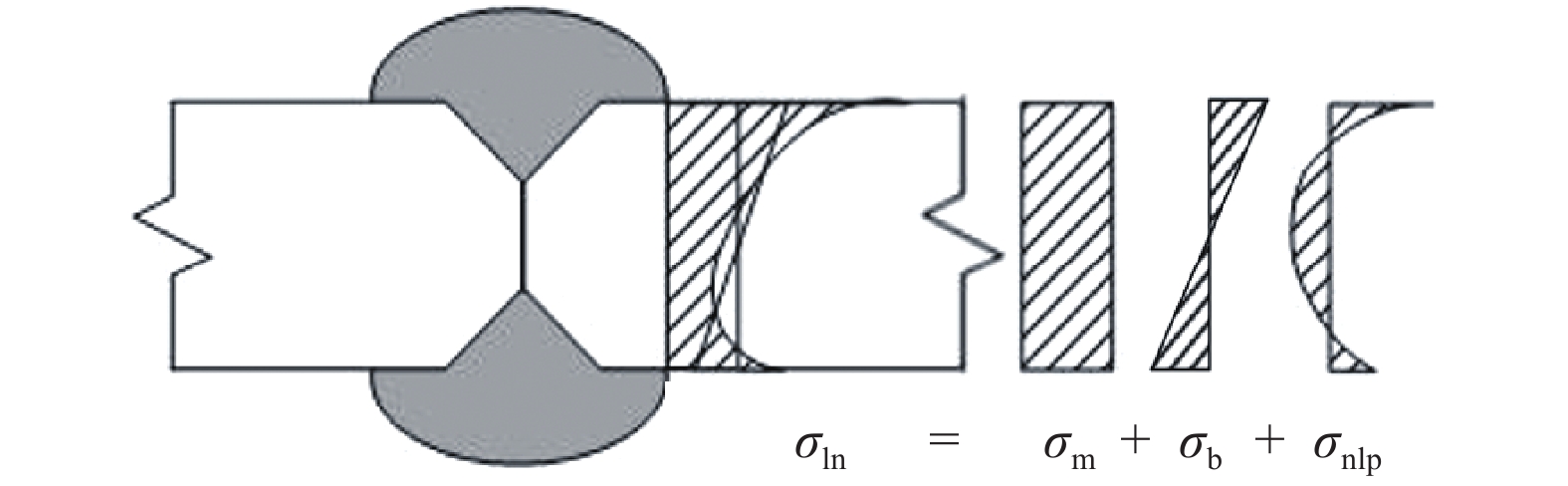
图3 热点处板厚方向典型的非线性应力分布
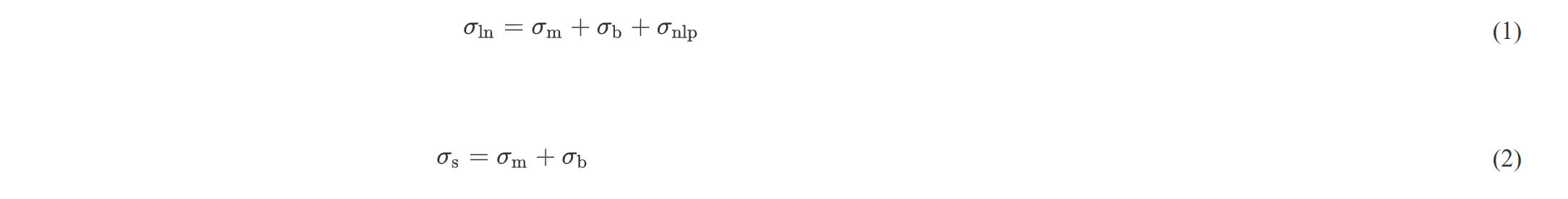
式中,σs为结构应力、σnlp为非线性应力峰值、σm和σb分别为膜应力和弯应力。
为了获得较为准确的热点应力值,通常使用热点应力外推法。其思想来源于实验测量方法[8],在焊趾端部一定距离内选取2~3个点,测量这些点的应变,从而换算得到其应力值,再使用外推的方法就能得到焊趾处的结构应力值,该值即为热点应力值,如图4所示。
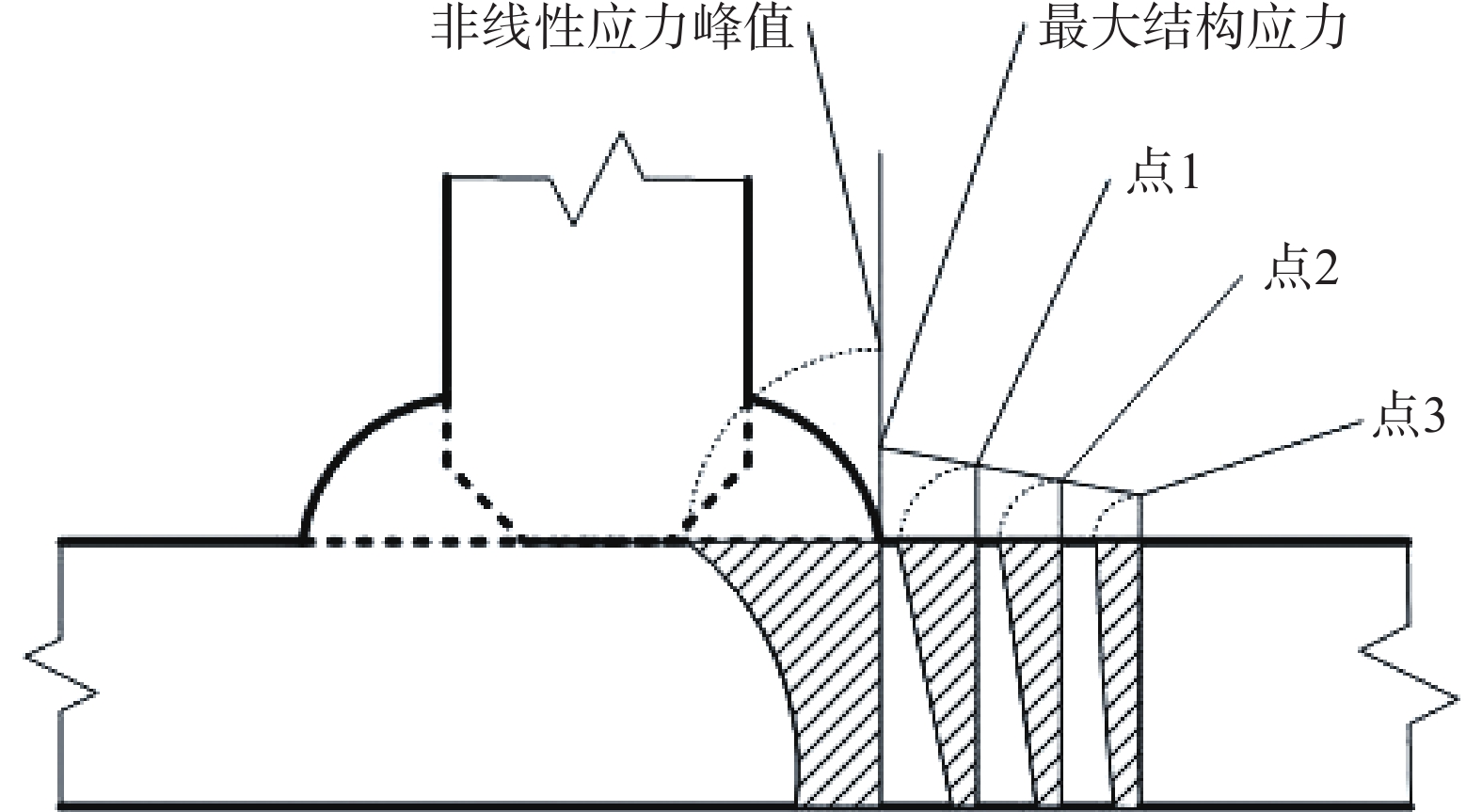
图4 测量结果线性外推
1点距离焊趾处的位置与板厚t和热点类型有关,一般热点在焊接结构上的位置有3种类型,如图5所示:“a”、“c”型热点位于板面上,“b”型热点位于板的边缘处。对于“a”、“c”型热点,参考点距离焊趾处的距离可以分为3种[9]:第1种是国际焊接协会推荐的0.4t、1.0t处选取2个参考点;第2种是船级社推荐在0.5t、1.5t处选取2个参考点;第3种是不需要外推直接选取距离焊趾处0.5t处的应力作为热点应力。其中第2种船级社推荐的方法比较适合在海洋工程中的焊接结构。而对于“b”型热点焊趾处的应力分布和t无关,而是在板面方向上分布,裂纹也沿着版面方向扩展,因此对于参考点的选取也和t无关,一般而言选取距离焊趾4、8和12 mm 3个点的应力值[10],再利用三点二次外推得到焊趾处的热点应力。
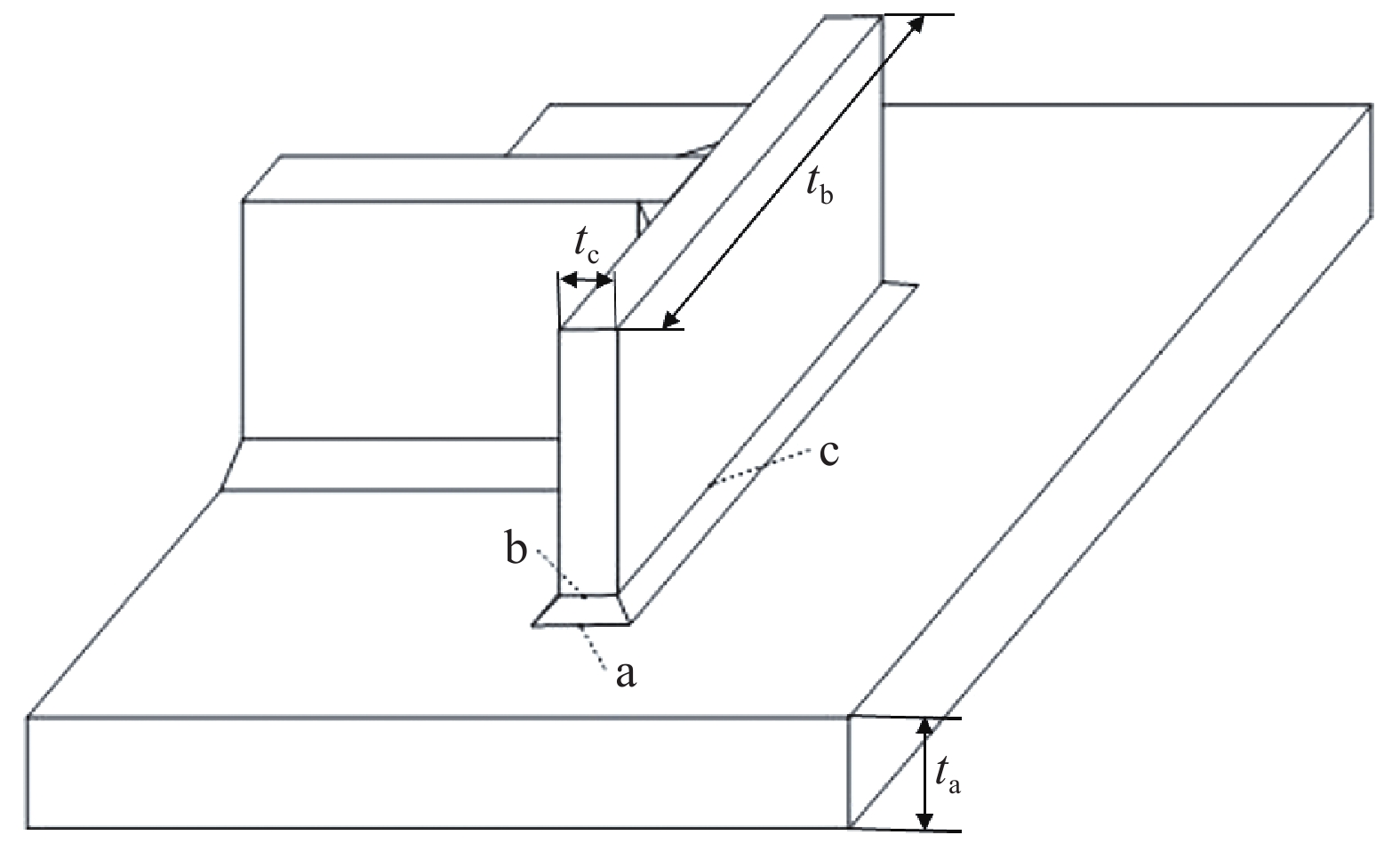
图5 焊接结构的热点类型
除了外推法,Fircke[9]在如何利用有限元分析来获得更精确的参考点应力值大小方面做了很多的工作,并取得了船级社的认可,在海洋工程上广泛使用。
同样借助有限元分析方法的厚度线性法(Through Thickness at the Weld Toe,TTWT)[11],把板厚方向上的应力分布线性化后得到的焊趾表面应力作为热点应力,如式(3)和(4)所示:
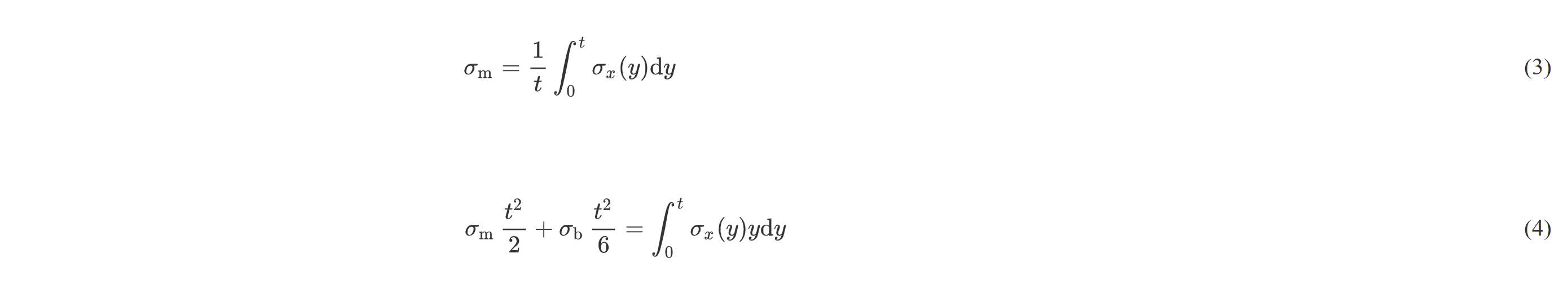
式中,σx(y)是板厚方向上的正应力分布。但TTWT法对有限元网格大小十分敏感,为了获得更接近真实的热点应力值,可以读取焊趾前端的应力值[12]。
为了克服TTWT法的上述缺点,Dong[13]提出热点应力可由焊趾前端沿着板厚方向上的应力分布获得,如图6所示。还考虑了剪应力的影响,该模型对二维试验有着较高的精度[14−15]。
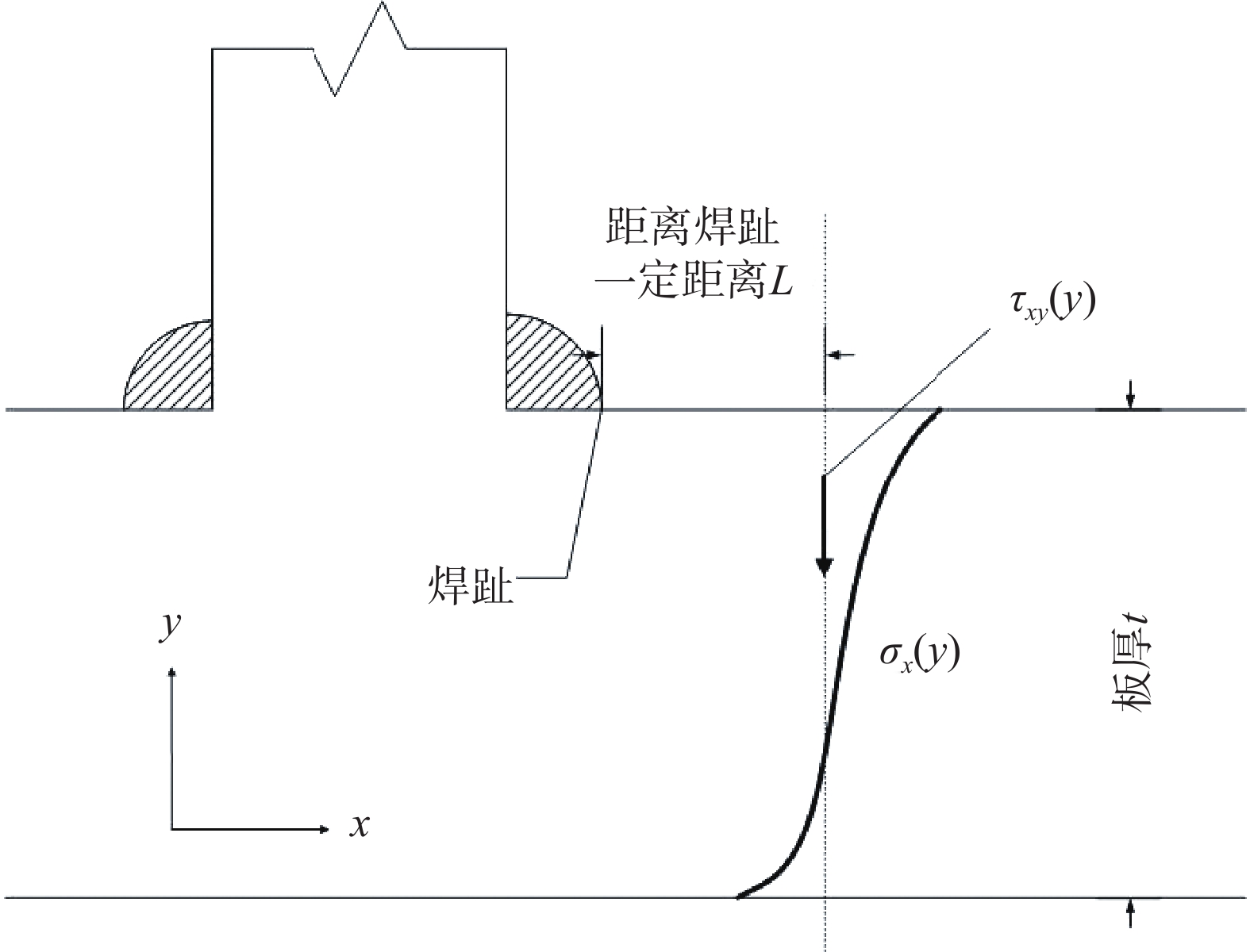
图6 板厚方向结构应力计算方法
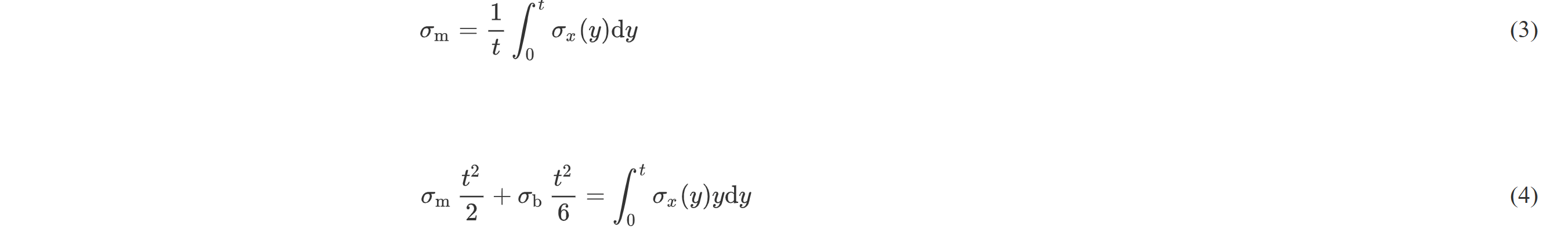
式中,L为距离焊趾的距离;τxy(y)为板厚方向上的切应力分布。
Xiao和Yamada[16]利用有限元方法发现焊趾部位的局部应力在板面方向距离焊趾2.5 mm处消失,在板厚方向距离焊趾1 mm处消失,而提出新的热点应力计算方法:“1 mm”法。该方法的热点应力选择的是板厚方向距离焊趾1 mm处的应力计算值,其在一定程度上考虑了厚度效应的影响,具有较高的精度。
1.3 局部法
1.3.1 缺口应力法
缺口应力法是以热点和结构应力法为基础发展而来的,以缺口处的非线性应力峰值为评估参量的方法。Neuber[17]的微观支持理论是将局部范围ρ∗内的平均应力作为缺口等效应力,分析方法是在缺口处建立一个虚拟圆弧,其半径为ρf,如图7所示,用该圆弧段内的最大应力值来代表约束微范围ρ∗内的平均应力值。虚拟半径ρf
和缺口半径的关系为
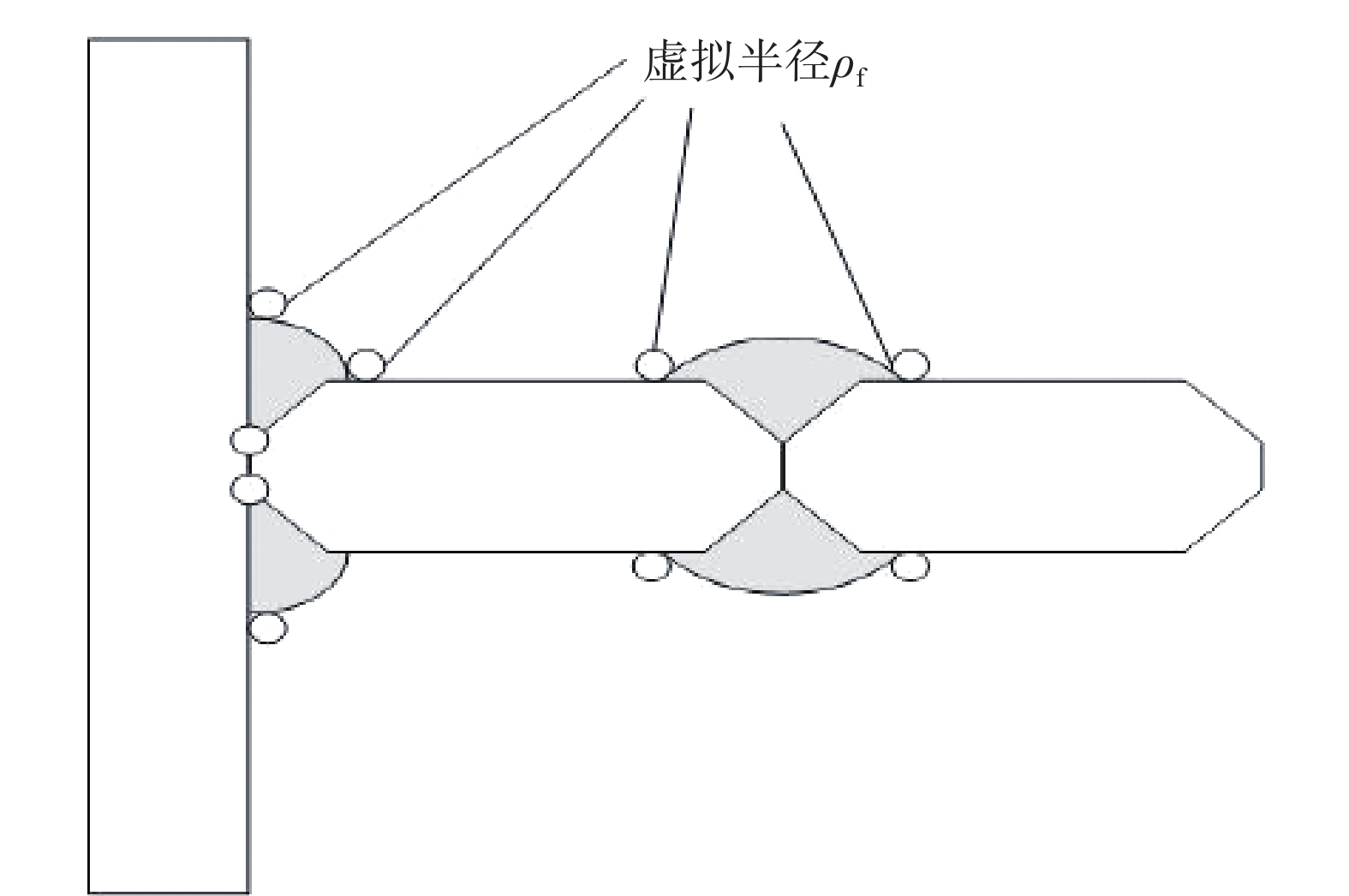
图7 虚拟圆弧定义

式中,S为缺口约束因子;ρ为实际缺口半径。
国际焊接协会建议:对于没有进行任何焊后处理的钢制焊接接头而言,焊趾实际情况十分恶劣,可视为实际缺口半径ρ=0;缺口约束因子S=2.5;约束范围ρ∗=0.4 mm,所以虚拟缺口半径则为ρf=1 mm。当焊接结构为厚度超过5 mm的钢板或铝板时,虚拟圆弧半径可取1 mm[18]。
1.3.2 临界距离法
缺口构件的疲劳强度取决于应力集中处一定距离范围内的应力水平,这个距离就叫做临界距离(Critical distance)。以该范围内的平均应力作为局部参量,当其大于临界值时即认为焊接结构会发生破坏,这就是临界距离法(Critical Distance Method, CDM),具体分为点(Point method, PM)、线(Line method, LM)、面(Area method, AM),其关键在于确定临界距离参数a0
,其值可由式(8)计算得到。

式中,ΔKth与Δσ0分别为给定循环特性R的光滑式样的疲劳裂纹扩展门槛值和疲劳极限[19]。
Taylor经过分析得到了当ΔKth=ΔK即疲劳裂纹扩展门槛值和等效应力强度因子相等时,PM、LM、AM法分别在距离裂纹尖端r=a0/2处的应力、r=~0~2a0线段上的平均应力、r=a0为半径的半圆形面积内的平均应力为Δσ0、Δσ0、1.1Δσ0[20]。这种方法还可适用于多轴应力和变幅应力状态下的疲劳研究[21]。
1.3.3 临界体积法
临界体积是指在应力集中处附近低于最大应力10%的三维区域,该区域内的平均应力决定疲劳损伤[22−23]。Qilafku[22]通过有限元分析指出在载荷模式和式样一定的情况下其临界体积是唯一的,同时还指出在给定疲劳寿命的情况下,有效剪切应力τef和平均正应力pm表示的疲劳强度是椭圆曲线(τef为横轴,pm为纵轴)如式(9)所示:

式中,a,b为材料常数。
在进行疲劳评定时利用光滑与缺口式样的扭转拉压试验的S–N曲线结合数值分析,确定材料常数a,b的值,得到不同疲劳寿命下的疲劳强度,再计算受载荷构件的τef与pm,并与之前的疲劳强度进行比较,从而来预测构建的疲劳寿命。Amarir等[24]利用临界体积法对汽车焊接结构进行疲劳寿命评定,得到了较为精确的结果,并指出临界体积法与现行应用标准中的其他方法相比具有许多优点。
2. 影响焊接结构疲劳寿命的因素
焊接结构的接头类型、焊接缺陷、残余应力、焊趾区几何形状等都会对疲劳寿命产生影响[25]。
2.1 接头类型
焊接接头处的应力集中,促进裂纹的萌生和扩展。在对接、十字和T型这3种接头中,对接接头的应力集中系数最小,是工程中常用的焊接接头;而另外2种接头由于焊缝处的截面变化较大,故应力集中系数较大,接头类型如图8所示。对于开坡口的十字接头,断裂只在焊趾处发生;对于不开破口的承载角焊缝十字接头,断裂也有可能在焊根处发生。
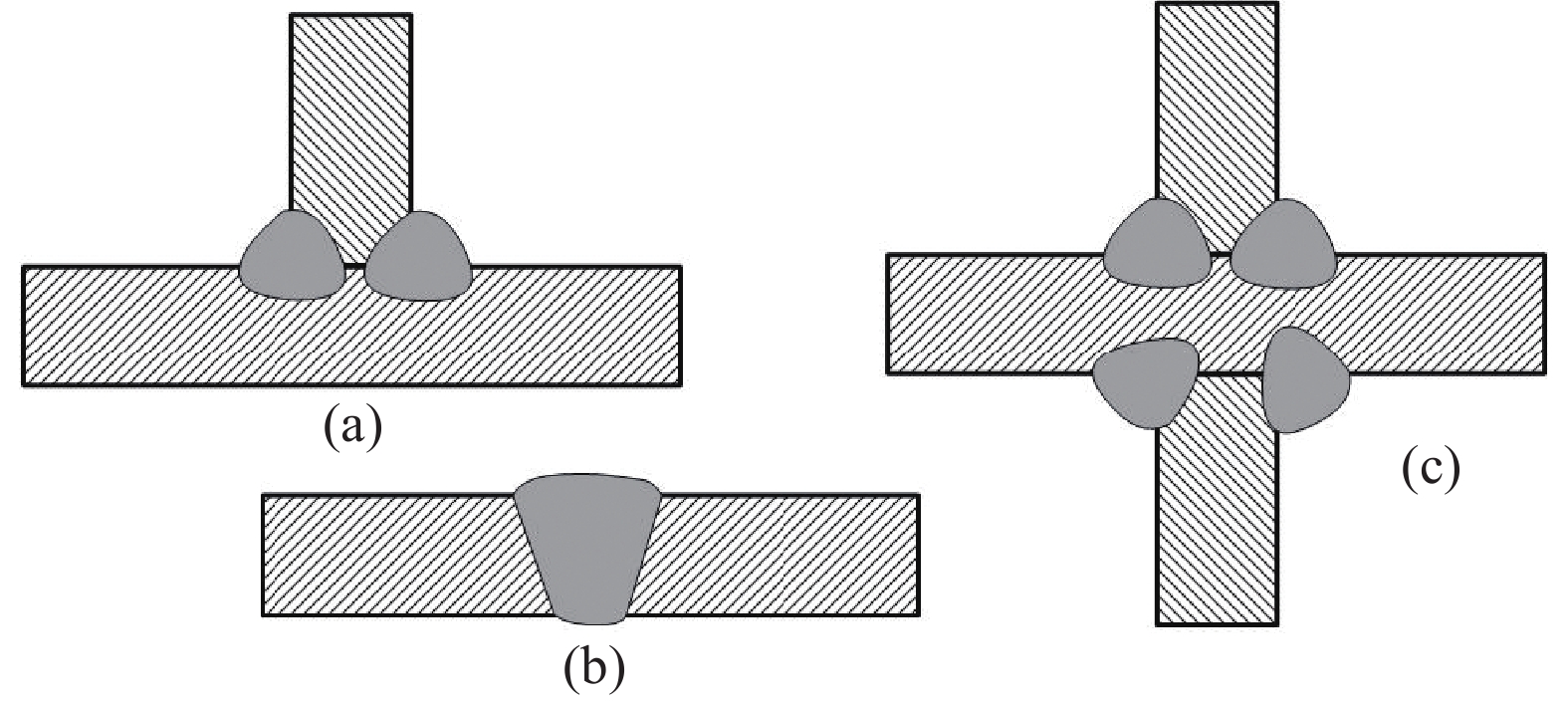
图8 接头类型:(a)T型;(b)对接;(c)十字
2.2 焊趾区几何形状
即使焊接材料和接头类型相同,焊接结构的疲劳寿命也会出现较大的差别,这是由焊趾区的几何外形不同造成的。有研究表明[2, 26−27],焊趾区的几何外形对疲劳性能的影响最大,并且这种影响随着母材的强度等级升高而增大。焊趾区的几何参数如图9所示。
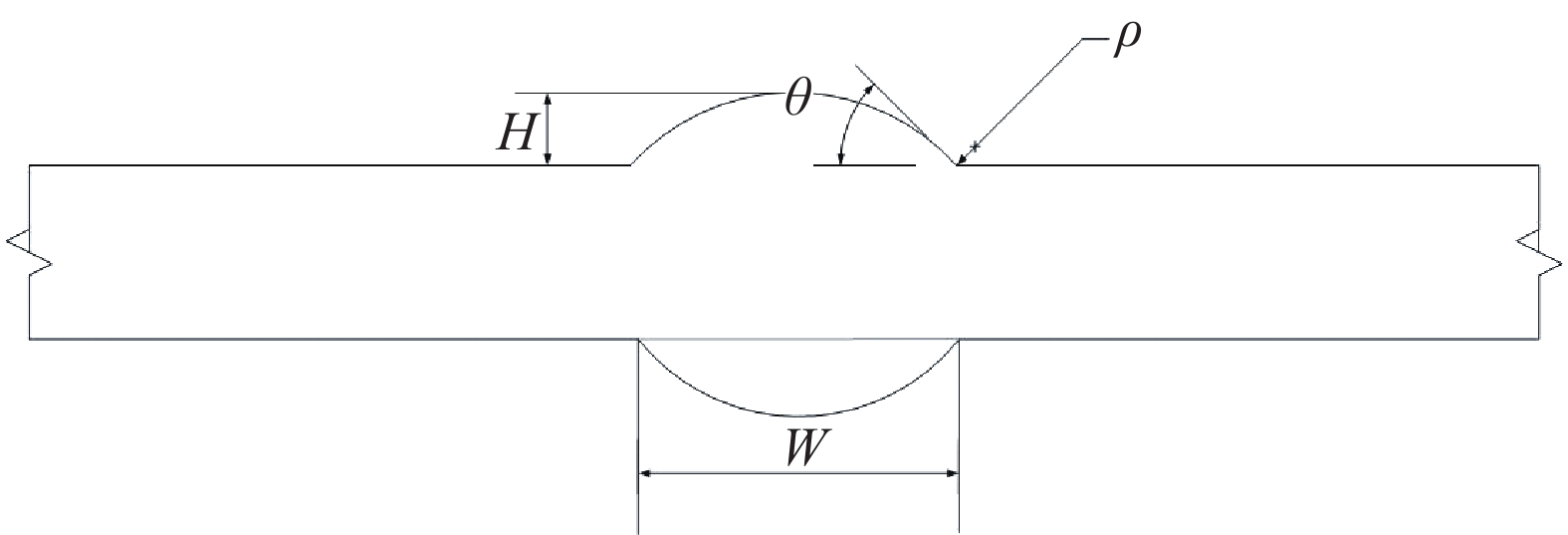
图9 焊趾区的几何参数
如图9所示,ρ和θ分别是焊趾区的过渡半径和倾斜角。有研究表明[27]:ρ的增加会降低应力集中,使疲劳强度增加;焊缝宽度W和焊缝高度H变化时,只要保持焊趾角度θ不变则应力集中系数不变,疲劳强度也不改变;而θ增加会使应力集中程度增大导致疲劳强度减小。
2.3 焊接缺陷
图10分别为裂纹、咬边、未焊透、气孔和夹杂,这些焊接缺陷都会造成应力集中,进而降低焊接结构的疲劳强度[28−29]。并且表面上的缺陷对疲劳寿命带来的影响比内部的缺陷更严重。
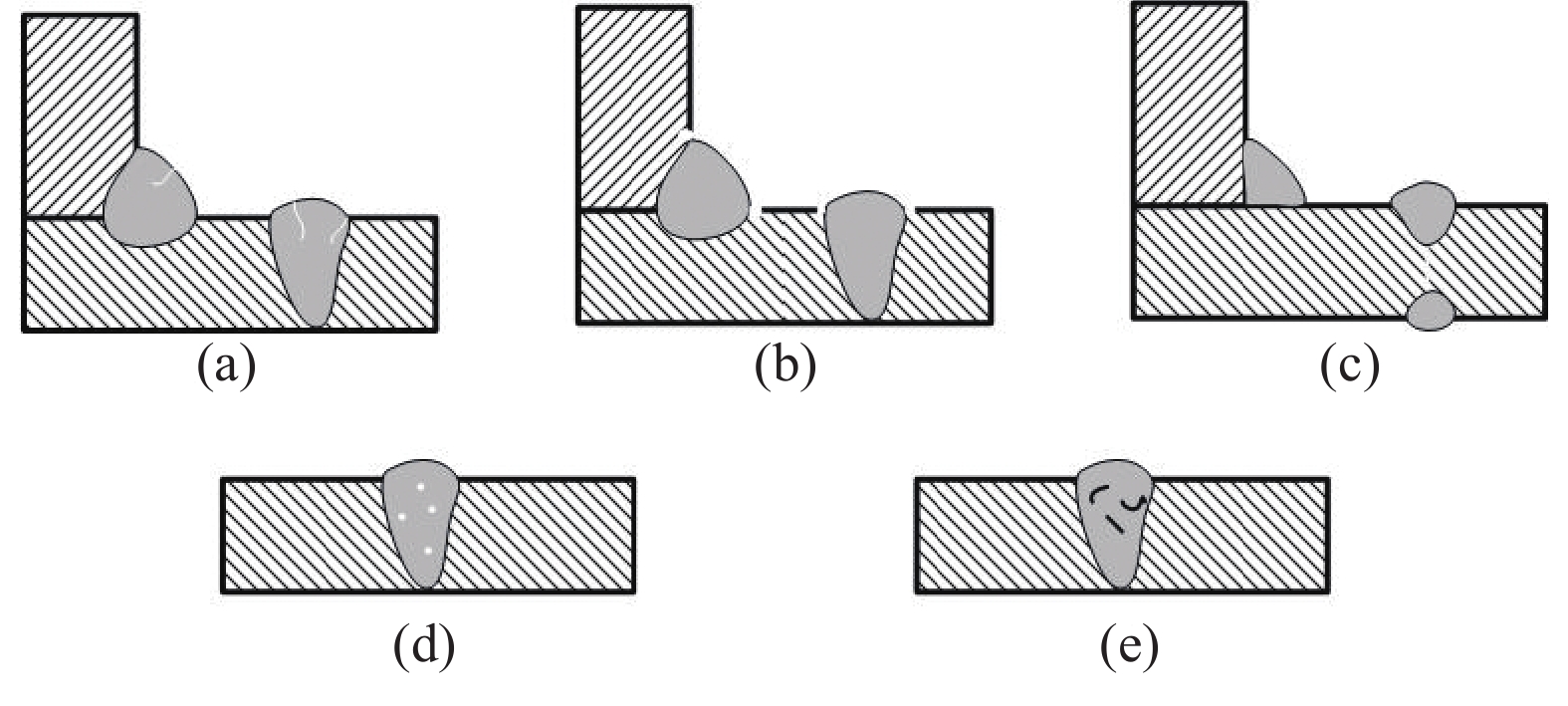
图10 焊接缺陷:(a)裂纹;(b)咬边;(c)未焊透;(d)气孔;(e)夹杂
2.4 焊接残余应力
焊接结构的焊缝及其附近区域的焊接残余应力可高至材料的屈服点,因此在施加循环载荷后[27],焊缝附近实际所承受的平均应力和应力峰谷值会高出很多,进而降低焊接结构的疲劳寿命,因为在载荷幅值相等的前提下,平均应力越大,焊接结构的疲劳寿命就越短,而焊接残余应力表现为拉应力,所以焊接结构会因为焊接残余应力的存在而大大降低其疲劳寿命[3, 30]。
3. 焊接结构的延寿方法
3.1 焊趾的打磨
当焊缝没有明显缺陷的条件下,用机加工的方式把焊缝的余高打磨平滑,可有效提升焊缝的疲劳强度。因为打磨焊缝的过程中去除了导致焊缝开裂的缺陷,同时也增大了焊趾的过渡半径ρ,如图11所示,减小了焊趾区的应力集中,进而提高了焊接结构的疲劳强度。但当焊缝处有未焊透以及裂纹时,打磨反而会使疲劳强度降低。无论何种接头类型,对焊趾打磨的方式都相同,但同样的打磨方式对于“对接”、“十字”和“T型”等不同的接头类型所带来的延寿效果有何差异目前并不明朗。
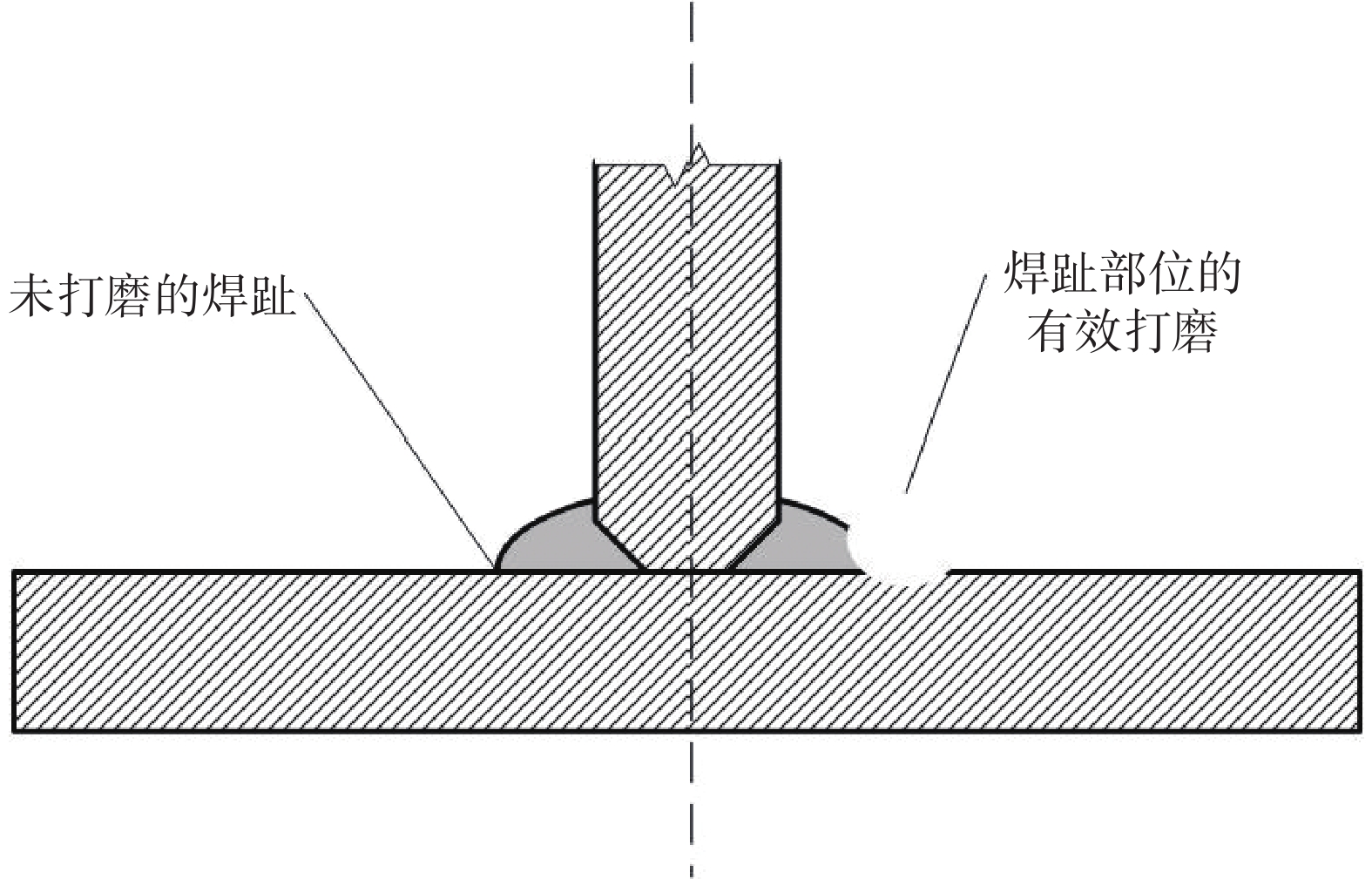
图11 打磨过程的基本要领
3.2 锤击和喷丸
在焊接结构焊缝及其附近引入压应力也是延长疲劳寿命的有效方法,因为压应力会减小材料所受到的循环载荷的平均应力,进而提高疲劳寿命。如图12所示,对焊趾反复锤击,引入残余压应力来降低平均应力,从而达到延寿的目的。

图12 焊趾锤击的效果图[31]
喷丸是通过喷枪喷出高速丸粒去轰击工件的表面,给工件表面引入残余压应力,起到延寿的效果[3]。
3.3 TIG熔修
TIG熔修的技术思路同焊趾打磨类似,目的是为了去除焊趾处的焊接缺陷和增大焊趾的过渡半径ρ,以减小应力集中系数,能有效延长疲劳寿命[32]。因为TIG焊接接头的质量好、疲劳强度很高,于是利用TIG焊炬对焊趾处一定范围内的金属重熔,以达到延寿目的。TIG熔修过程示意图如图13所示。
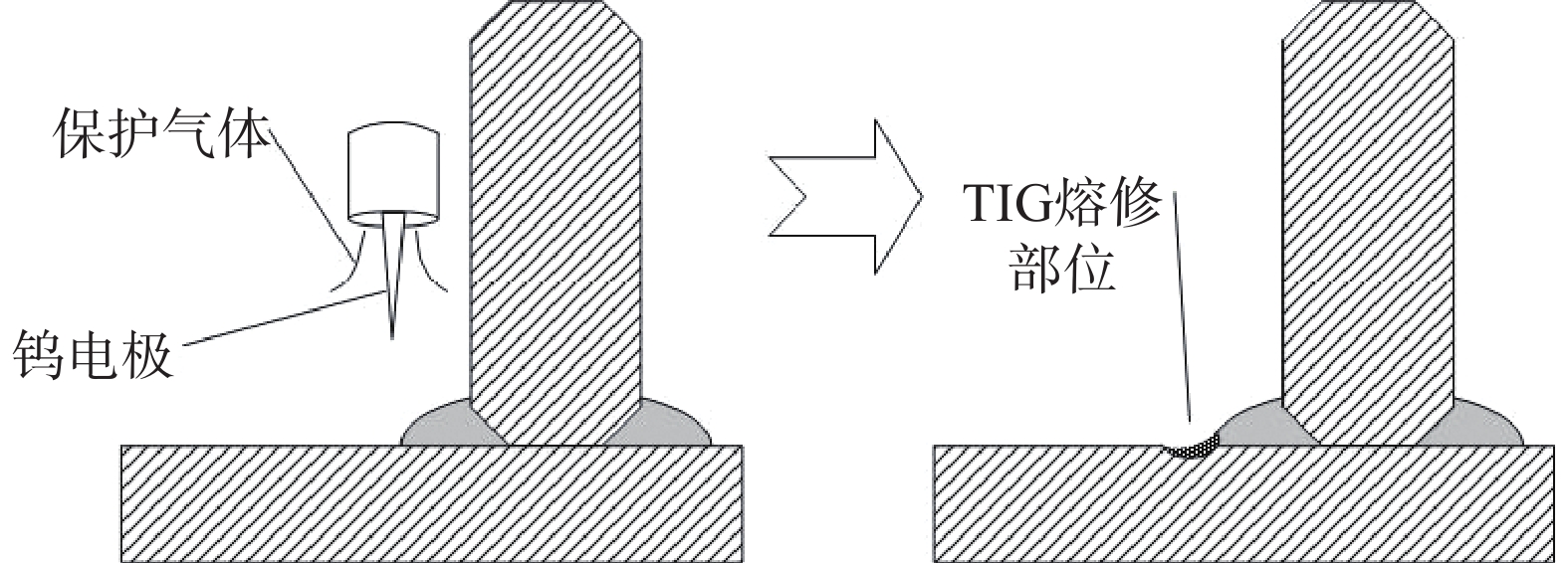
图13 TIG熔修示意图
4. 结束语
名义应力法是最早应用在焊接结构疲劳评定的方法,名义应力法相对简单,对简单焊接结构的疲劳进行评估较为简便,但精度偏低,且难以评定复杂焊接结构。热点应力法精度比名义应力法高,由于无需考虑焊缝细节,所以当接头类型相同时,可用同一条S–N曲线,但只能评估焊趾处的应力状态,被大量应用在海洋工程领域。局部法的评定精度与复杂程度都高于前两者,所反映的应力状态也更加准确。通过打磨和TIG熔修消除焊接缺陷和增大焊趾过渡半径ρ,通过锤击和喷丸引入残余压应力,这些延寿措施可以消除或者缓解各种缺陷对寿命带来的不利影响。
目前,在焊接结构单轴疲劳评定方面已有大量的研究,也发展出了许多评定方法。但在实际工程应用中,大部分的焊接构件承受的并非单轴载荷,而是复杂交变的多轴载荷。关于焊接结构多轴疲劳的评定还处于研究初期,疲劳评定体系不完善,相应的研究工作远远不足,因此针对焊接结构的多轴疲劳问题还应继续深入研究,以期能找到用于焊接结构多轴疲劳评定的有效方法。
参考文献
[1]Muzaffer S, Chang K H, Wang Z M, et al. Comparison of stiffener effect on fatigue crack in KT-type pipe joint by FEA. Weld World, 2022(66): 783
[2]霍立兴. 焊接结构的断裂行为及评定. 北京: 机械工业出版社, 2000
[3]陈传尧. 疲劳与断裂. 武汉: 华中科技大学出版社, 2002
[4]Fricke W. Fatigue analysis of welded joints: State of development. Mar Struct, 2003, 16(3): 185 DOI:10.1016/S0951-8339(02)00075-8
[5]崔维成,蔡新刚,冷建兴. 船舶结构疲劳强度校核研究现状及我国的进展. 船舶力学,1998(4):63
[6]陈科,王峰. 结构有限寿命设计法:名义应力法. 中国重型装备,2010(2):1 DOI: 10.3969/j.issn.1674-0963.2010.02.001
[7]Kim M H, Kim S M, Kim Y N, et al. A comparative study for the fatigue assessment of a ship structure by use of hot spot stress and structural stress approaches. Ocean Eng, 2009, 36(14): 1067 DOI: 10.1016/j.oceaneng.2009.07.001
[8]Radaj D, Sonsino C M, Fricke W. Fatigue assessment of welded joints by local approaches. Cambridge: Woodhead Publishing Limited, 2006
[9]Fricke W. Recommended hot-spot analysis procedure for structural details of ships and FPSOs based on round-robin FE analyses. Int J Offshore Polar. 2002, 12(1): 40
[10]Niemi E, Fricke W, Maddox S J. Fatigue analysis of welded components: Designer's guide to the structural hot-spot stress approach. Cambddge: Woodhead Publishing Limited, 2006
[11]Radaj D. Design and analysis of fatigue resistant welded structures. Cambridge: Abington Publishing, 1990
[12]Poutiainen I, Tanskanen P, Marquis G. Finite element methods for structural hot spot stress determination: A comparison of procedures. Int J Fatigue, 2004, 26(11): 1147 DOI: 10.1016/j.ijfatigue.2004.04.003
[13]Dong P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int J Fatigue, 2001, 23(10): 865 DOI: 10.1016/S0142-1123(01)00055-X
[14]Kyuba H, Dong P. Equilibrium-equivalent structural stress approach to fatigue analysis of a rectangular hollow section joint. Int J Fatigue, 2005, 27(1): 85 DOI: 10.1016/j.ijfatigue.2004.05.008
[15]Doerk O, Fricke W, Weissenborn C. Comparison of different calculation methods for structural stresses at welded joints. Int J Fatigue, 2003, 25(5): 359 DOI: 10.1016/S0142-1123(02)00167-6
[16]Xiao Z G, Yamada K. A method of determining geometric stress for fatigue strength evaluation of steel welded joints. Int J Fatigue, 2004, 26(12): 1277 DOI: 10.1016/j.ijfatigue.2004.05.001
[17]Radaj D, Lazzarin P, Berto F. Generalised Neuber concept of fictitious notch rounding. Int J Fatigue, 2013, 51: 105 DOI: 10.1016/j.ijfatigue.2013.01.005
[18]Fricke W. Guideline for the fatigue assessment by notch stress analysis for welded structures//Annual Assembly of International Institute of Welding. Graz, 2008
[19]Taylor D, Bologna P, Knani K B. Prediction of fatigue failure location on a component using a critical distance method. Int J Fatigue, 2000, 22(9): 735 DOI: 10.1016/S0142-1123(00)00062-1
[20]Taylor D. Geometrical effects in fatigue: a unifying theoretical model. Int J Fatigue, 1999, 21(5): 413 DOI: 10.1016/S0142-1123(99)00007-9
[21]杨新岐,张艳新,霍立兴,等. 焊接接头疲劳评定局部法研究进展. 机械强度,2003(6):675 DOI: 10.3321/j.issn:1001-9669.2003.06.018
[22]Qilafku G, Kadi N, Dobranski J, et al. Fatigue of specimens subjected to combined loading. Role of hydrostatic pressure. Int J Fatigue, 2001, 23(8): 689
[23]Sonsino C M, Radaj D, Brandt U, et al. Fatigue assessment of welded joints in AlMg 4. 5Mn aluminium alloy (AA 5083) by local approaches. Int J Fatigue, 1999, 21(9): 985
[24]Amarir I, Mounir H, Marjani A E. Compilation of fatigue assessment procedures of welded structures for automotive utilization. Mech Based Des of Struc, 2020, 50(7): 1
[25]张彦华,刘娟,杜子瑞,等. 焊接结构的疲劳评定方法. 航空制造技术,2016(11):51 DOI: 10.16080/j.issn1671-833x.2016.11.051
[26]王立君. 焊趾缺口效应及其疲劳裂纹扩展的统计分析. 天津: 天津大学, 1990
[27]Haagensen P J, Maddox S J. IIW recommendations on methods for improving the fatigue lives of welded joints. Cambridge: Woodhead Publishing Limited, 2013
[28]Wang D, Yao D D, Gao Z B, et al. Fatigue mechanism of medium-carbon steel welded joint: Competitive impacts of various defects. Int J Fatigue, 2021, 151: Art No. 106363
[29]Shin W S, Chang K H, Muzaffer S. Fatigue analysis of cruciform welded joint with weld penetration defects. Eng Fail Anal, 2021, 120: Art No. 105111
[30]Mo T, Chen J Q, Zhang P J, et al. Numerical simulation of the effect of ultrasonic impact treatment on welding residual stress. Int J Mod Phys B, 2021, 35(17): Art No. 2150175
[31]王东坡,龚宝明,吴世品,等. 焊接接头与结构疲劳延寿技术研究进展综述. 华东交通大学学报,2016,33(6):1
[32]李瑞武,孙朋朋,李鹏,等. 焊趾TIG重熔对钛合金T型接头疲劳性能影响. 材料开发与应用,2017,32(5):41
作者简介:易竺霖(1998—),男,汉族,四川巴中人,在读硕士研究生,研究方向:焊接结构的疲劳研究。通信地址:中国船舶集团第七二五研究所(洛阳);E-mail:zhulinyi8816@163.com




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国