"巨人国"的怪兽是否站立起来？

今天我们要来聊聊一个既科学又有趣的话题——“标度律”。别被这个高大上的名字吓到，其实它就像是我们日常生活中的“放大镜”，只不过它放大的不是物体的尺寸，而是物体之间那些微妙而有趣的关系。

首先给大家讲故事。放大一百倍的蜘蛛，为什么会被自己压垮？

一、蜘蛛放大的“悲剧”

在科幻影视作品中，常常会看到小人国和巨人国，或者会看到各种体型巨大的怪兽，比如放大100倍的蜘蛛（图1）。看到这些，你可能会说：“哇，一只巨大的蜘蛛，可以轻松地捕食小鸟和小老鼠啦！”

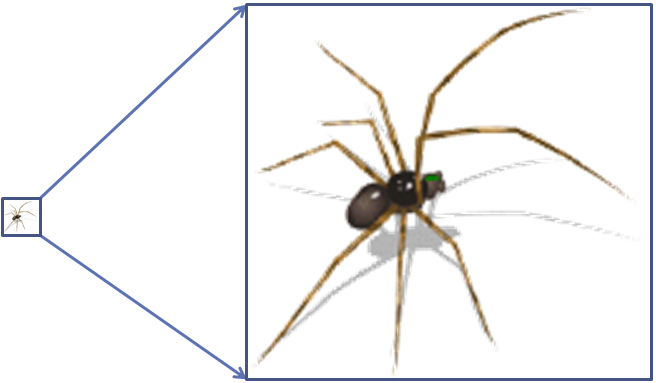
图1 放大100倍的蜘蛛

但事实真的如此吗？

让我们用“标度律”这把“放大镜”来仔细瞧瞧。首先，从几何上来看，当蜘蛛被放大100倍时，它的体积会变为原来的1003倍，即1000000倍；而它的腿粗（横截面积）会变为原来的1002倍，即10000倍，就是说形体上具有“几何相似性”。从受力分析来看，腿部单位横截面积承受的体重压力（即压应力）增大了1003÷1002=100倍。这意味着，虽然蜘蛛的体型变大了，但它的腿和身体的承重能力并没有按同样的比例增强。

换句话说，蜘蛛的体重增长得比它的腿能承受的重量还要快！这就像你突然增加了很多体重，但你的腿还是原来的粗细，结果可想而知——你的腿很可能会被压折。

所以，放大100倍的蜘蛛，最终可能会因为无法支撑自己巨大的体重而被压垮。这听起来是不是既意外又有趣？

有兴趣的同学可以参看我的个人微信公众号“医用生物力学”的文章：猪鼻子插葱——装象。那里面提到了相似性原理，包括几何相似性和力学相似性。力学相似性关注模型与实物之间在力学特性上的比例关系，它与标度律都涉及到系统中物理量之间的比例关系。力学相似性原理可以应用于验证标度律。

接下来看看什么是标度律。

二、标度律是什么？

简单来说，标度律就是描述当系统中的一个量（比如长度、质量、时间等）发生变化时，其他相关量会如何按比例变化的一种规律。

在自然界中，许多现象都遵循着标度律，它们就像是大自然的“密码”，等待着我们去破解。

1.标度律的数学表达

标度律在数学上通常表示为Y=cX^k的形式，其中Y和X是相关的物理量，c是一个常数，k是标度指数。这个k值非常关键，它决定了Y随X变化的速率。

当k=1时，我们称之为线性关系。这意味着Y和X的增长速度是相同的，比如你赚的钱越多，能买的东西也越多，这就是一个线性关系。

当k>1时，我们称之为超线性关系。这意味着Y的增长速度比X还要快，就像复利投资一样，时间越长，收益增长得越快。

当k<1时，我们称之为亚线性关系。这意味着Y的增长速度比X要慢，就像你跑步时，随着距离的增加，你的速度可能会逐渐下降。

标度律在自然界中普遍存在，从地震的频率与震级之间的关系，到城市的人口分布与规模之间的关系，再到互联网的流量分布与用户行为之间的关系……几乎无处不在。它就像自然界的“万能钥匙”，揭示着许多看似无关实则紧密相连的现象背后的秘密。

这种普遍性并不是偶然的，而是源于幂律关系所描述的复杂系统的内在特性。在复杂系统中，各个部分之间往往存在着复杂的相互作用和依赖关系，这种关系使得系统的整体行为呈现出幂律分布的特征。

2.标度律的表现形式

等速生长和异速生长标度律是标度律的两种表现形式。

等速生长标度律指的是生物体在生长过程中，各个部分与整体之间保持恒定的比例关系。这种生长方式遵循几何相似性，即生物体的大小在生长过程或进化过程中呈比例关系变化。在上述标度律的数学表达式中，k=1即表示等速生长标度律。一个典型的例子是青蛙，在变态后的短时间内，青蛙的腿总是与其身体呈正比例速率变化。等速生长由伽俐略的平方-立方律决定，即一个机体如果在长度上等速缩放地成倍增长，则其表面积将会增长4倍，而其体积和体重将会增长8倍。然而，这种生长方式在实际生物体中并不常见，因为它可能导致生物体在生长过程中遇到生理和机械上的限制，比如上述蜘蛛放大的“悲剧”。

异速生长标度律则是指生物体在生长过程中，各个部分与整体之间的比例关系发生变化。这种生长方式不遵循几何相似性，而是表现为一种非线性的比例关系。在上述标度律的数学表达式中，k≠1即表示异速生长标度律。在生物学中，异速生长标度律具有广泛的应用和重要的生物力学意义。它揭示了生物体在生长过程中，各个部分与整体之间如何协调变化以适应环境和功能的需求。例如，随着生物体重量的增加，其代谢率并不呈线性增长，而是遵循一个约为3/4的幂律关系（克莱伯定律），这反映了生物体在能量利用和分配上的优化策略。通俗地说，标度律是结构优化、节能高效的体现。比如，一个成人与他幼儿时相比，体积重量增长了十几甚至几十倍，可心脏的增长并没有这么大，他的饭量也没增长那么多呢。

由于异速生长标度律更为普遍，所以一般所说的标度律就是指异速生长标度律。

3. 标度不变性：自然界的“自相似性”

幂律关系还有一个非常有趣的特性，那就是标度不变性。这意味着，无论你是观察系统的整体还是局部，它们所遵循的幂律关系都是相同的。换句话说，系统在不同尺度下呈现出自相似性，展示了自然界的“几何奇迹”。

这种自相似性在自然界中非常普遍，比如闪电、水滴、雪花、树木、花草、海螺、河流、海岸线、山脉、云朵、大脑、血管网络等等，甚至在社会学中也普遍存在，比如股票走势等。它们的形状和分布在不同尺度下都呈现出相似的特征（图2）。

图2 植物形状和分布在不同尺度下都呈现出相似的特征

分形现象是一种具有自相似特性的图形或结构。分形通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状” （图3）。

图3当无限放大科赫曲线时，它会展示出无限重复的自相似性

分形理论不仅揭示了自然界中复杂几何形状和结构的内在特性，还为我们提供了一种简洁而有效的描述复杂系统的方法。通过忽略系统的具体细节，只关注其整体行为所遵循的分形规律，我们可以用分形理论来更好地理解和预测系统的行为。

看到这里，我就疑惑啦：我自己的自相似性是什么？我是无数个不同的“小我”堆砌而成的吗？我有无数个“同我”个体吗？我和他们是否共同组合成了一个“大我”呢？

三、生物力学中的标度律

接下来，让我们把标度律这把“放大镜”对准生物力学这个有趣的领域。

生物力学是应用力学原理和方法对生物体中的力学问题定量研究的科学。在这个领域里，标度律同样发挥着重要的作用。下面举例说明。

1.血管网络与分形

首先，我们来看看生物体内的血管网络。血管网络是一个典型的分形结构，这意味着它的每一个部分都与整体有着自相似性。换句话说，无论你是观察一根细小的毛细血管还是整个心脏的大血管，抑或是观察肺部的支气管或者血管，它们的形状和分布都遵循着相同的规律（图4）。

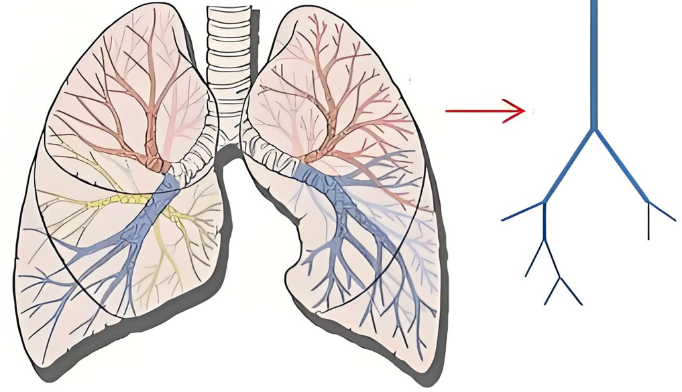
图4 肺部的支气管或者血管分布

血管网络的这种分形结构，使得生物体能够高效地输送氧气和营养物质到身体的每一个角落。而这种高效性，正是得益于血管网络遵循的标度律。

举个例子来说，大象的体重是人的几千倍，但它们的血管网络却能够以惊人的效率为如此庞大的身体提供足够的氧气和营养物质。这正是因为它们的血管网络遵循着特定的标度律，使得血管半径和血流量能够随着体重的增加而按比例调整。

经动物实验验证，心肌质量与冠脉血流量之间的关系满足异速生长律，即Qcor=kMmyo0.75，其中Qcor为冠脉血流量，Mmyo为心肌质量，k是比例系数，因个体而异。根据此模型，可以由某一支冠脉血流量来计算供应其下游的心肌质量（图5），就像知道了农田灌溉的水管流量有多大就能知道能灌溉多少农田。

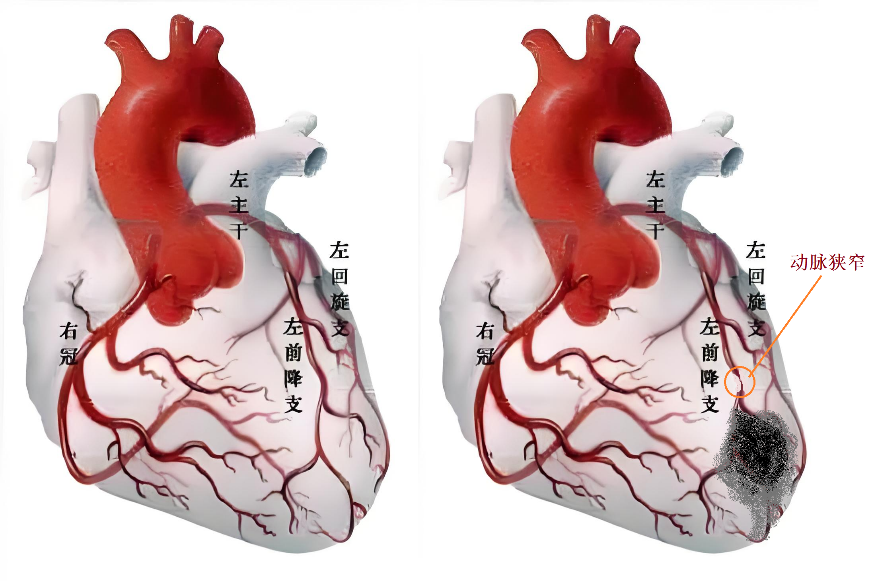
图5 冠脉分支血流量灌注下游心肌

2.基础代谢率与体重

基础代谢率（BMR）是指人体在清醒而又极端安静的状态下，不受肌肉活动、环境温度、食物及精神紧张等影响时的能量代谢率。它决定了生物体维持生命活动所需的能量多少。

基础代谢率与体重之间并不是简单的线性关系，而是一种幂律关系，即代谢率与体重的某个幂次成正比。这种关系被称为大名鼎鼎的代谢标度律或克莱伯定律。

克莱伯定律指出，对于大多数生物体来说，它们的代谢率与体重的3/4次幂成正比，即前文所述标度律的数学表达变为q=M^(3/4)，其中q为代谢率，M为体重（图5）。这意味着，如果一个生物体的体重增加了一倍，它的代谢率并不会增加一倍，而是只增加大约80%（因为234≈1.8）。体重增加10倍，代谢率只增加约5.6倍。

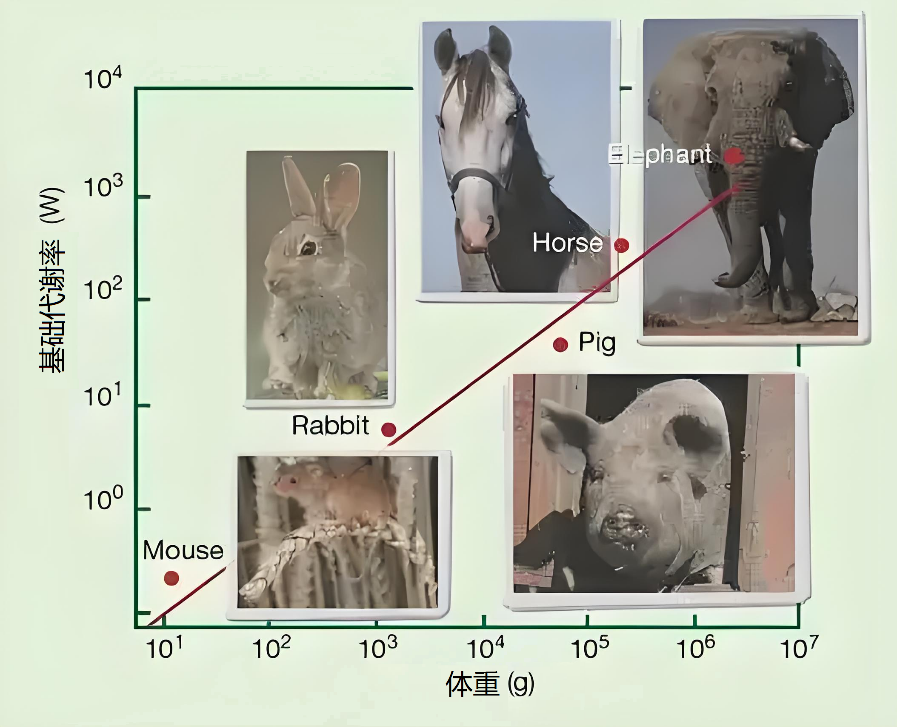
图5 “鼠象线”成为生物能学中最重要和最著名的概括之一。在各种不同体型的动物中，代谢率与体重的0.75次方成正比。

这个定律听起来可能有些抽象，但我们可以通过一个简单的例子来理解它。一只大象和一只老鼠相比，大象的体重是老鼠的几万分之一，但它们的代谢率却并不是相差几万倍。相反，根据克莱伯定律，大象的代谢率只比老鼠高几千倍。这是因为大象的细胞数量虽然比老鼠多得多，但每个细胞所需的能量却相对较少。这是因为大象的身体结构更加优化，能够更好地利用能量进行生命活动。

克莱伯定律不仅揭示了生物体代谢率与体重之间的内在联系，还为我们理解生物体的能量利用效率和生长策略提供了重要的线索。

3.生物力学性能

骨骼的强度就遵循着特定的标度律。随着生物体体重的增加，它们的骨骼也会变得更加粗壮和坚固，以支撑更大的体重。这种变化并不是随意的，而是遵循着特定的幂律关系。

前面讲了放大100倍的蜘蛛的故事，其背后就是标度律在起作用。因为体积和重量是三维量，而横截面积是二维量，所以随着生物体体积的增大，其支撑结构（如腿）需要按标度律来增粗，以保持结构的稳定性。这就像是建造高楼大厦需要更坚固的地基一样。

同样地，肌肉的收缩力也与肌肉的横截面积和纤维类型等因素遵循着特定的标度律。这使得生物体能够根据不同的运动需求调整肌肉的力量和耐力。

4.标度律的科学意义

现在，我们已经通过一些生动的例子了解了标度律及其在生物力学中的应用。那么，标度律到底有什么科学意义呢？

首先，标度律有助于我们理解自然界中复杂系统的行为规律。无论是生物体内的血管网络、代谢过程还是骨骼肌肉系统，它们都遵循着特定的标度律。这些规律不仅揭示了生物体结构和功能之间的内在联系，还为我们理解生物体的进化、适应和生存策略提供了重要的线索。

其次，标度律在数学和物理学中也有着广泛的应用。它们为我们提供了一种简洁而有效的描述复杂系统的方法，使得我们能够更好地预测和控制系统的行为。

最后，标度律还有助于我们推动科技进步和创新。通过对标度律的深入研究，我们可以开发出更加高效、节能和环保的技术和产品，为人类的可持续发展做出贡献。

四、标度律在科学研究中的应用

标度律及其相关的幂律关系、标度不变性和分形理论在自然科学与社会科学研究中都有着广泛的应用。

1. 生态学与生物多样性

在生态学中，标度律被用来研究物种分布、生物多样性和生态系统功能之间的关系。比如，物种数量与岛屿面积之间的关系就遵循幂律分布，这被称为“岛屿生物地理学理论”。研究发现，岛屿上的物种数量与岛屿面积的某个幂次成正比，这个幂次通常在0.2到0.35之间。这个规律不仅适用于自然岛屿，也适用于城市绿地、自然保护区等人工生态系统。通过了解这种标度关系，生态学家能够更好地预测和保护生物多样性。

2. 地震学

在地震学中，标度律被用来研究地震的频率与震级之间的关系。著名的古登堡-里克特定律就是一个幂律关系，它指出地震的频数与震级之间的关系遵循指数分布。具体来说，较大震级的地震发生的频率远低于较小震级的地震，而这种关系可以用幂律来描述。通过对地震数据的统计分析，地震学家能够更好地理解地震活动的规律，为地震预测和防灾减灾提供科学依据。

3. 社会学与城市发展

在社会学中，标度律被用来研究城市的人口分布、经济发展和社会结构之间的关系。比如，齐普夫定律指出，城市的大小（通常以人口数量来衡量）与其排名之间的关系遵循幂律分布。具体来说，排名第二的城市人口是排名第一的城市人口的一半，排名第三的城市人口是排名第一的城市人口的三分之一，以此类推。这个规律不仅适用于城市人口，也适用于其他许多社会现象，如公司规模、语言使用频率等。这就是“集约化”产生的规模效应。通过对这些标度律的研究，社会学家能够更好地理解城市发展的动力机制和社会结构的演变规律。

4. 物理学与材料科学

在物理学和材料科学中，标度律被用来研究材料的力学性能、热学性能和电学性能等随尺寸变化的关系。比如，在纳米尺度下，材料的许多物理性质都会发生显著的变化，这种变化往往遵循幂律关系。通过对这些标度关系的研究，物理学家和材料科学家能够设计出具有特殊性能的新材料，为纳米技术和新材料的发展提供理论支持。

五、标度律的未来展望

标度律作为一种强大的工具，已经在多个领域取得了显著的成果。然而，随着科学技术的不断进步和数据量的爆炸式增长，标度律的应用前景仍然十分广阔，未来可期。

跨学科融合：标度律作为一种通用的描述复杂系统的方法，有望在物理、化学、生物、社会学等多个学科之间建立更加紧密的联系，推动跨学科的研究和合作。

数据驱动的科学发现：随着大数据和人工智能技术的发展，我们可以利用更加先进的数据处理和分析方法来研究标度律，揭示隐藏在数据背后的更深层次的规律。

新材料与新技术：通过对标度律的深入研究，我们可以设计出具有特殊性能的新材料和新技术，为能源、医疗、环保等领域提供创新性的解决方案。

政策制定与社会管理：标度律也可以应用于政策制定和社会管理领域，帮助我们更好地理解社会现象的本质和规律，为政策的制定和实施提供科学依据。

总之，标度律作为一种描述复杂系统行为的重要工具，已经在多个领域取得了显著的成果。随着科学技术的不断进步和数据量的爆炸式增长，标度律的应用前景将更加广阔。让我们期待标度律在未来继续为我们揭示自然界的奥秘，推动科学技术的进步和社会的发展。

六、小结

标度律，听起来高深莫测，其实就像是自然界的“万能钥匙”。简单来说，标度律揭示了生物体的大小与其某些物理量（如体重、力量等）之间的特定关系。在生物力学领域，标度律更是无处不在。不论是血管网络，还是肌肉、骨骼，抑或新陈代谢，都遵守标度律的法则。大象比老鼠虽然体型庞大、吃得多，但它每个细胞的耗能却比老鼠的细胞低，真是“大个子也有小秘密”。

标度律就像是自然界的“大小魔法师”，它让蚂蚁能成“大力士”，却让大象无法成为“跳跃冠军”。它告诉我们：在生物界，不是大就一定强，得按规矩（标度律）来！

所以，下次当你看到小蚂蚁轻松举起比自己重几倍的食物时，或者惊诧于跳蚤跳的高度远远超过自身高度上百倍时，或者感叹于自己“喝水都长肉”而为增重肥胖烦恼时（图6），别忘了“感谢”标度律，它让这个世界充满了奇妙又有理。

图6 “喝水都长肉”？我不怕——只要赘肉长在别人身上！被体重压折的又不是我的腿。