【北京中轴线】颐和园玉带桥护栏的垂链线发现

悬链线在北京古桥中的一个应用发现

作者：王锐英

悬链线的曲线形式在北京古桥中存在吗？笔者考察后有一个发现，就是颐和园的玉带桥和绣漪桥的汉白玉栏杆，在其桥顶圆弧曲线切点向下至桥头之间的中段栏杆应该呈现为悬链线形式，上接桥顶的圆弧曲线，下接桥头的斜坡直线，形成反向渐变过渡的柔美线形，极大地增强了桥梁玉带般轻柔飘逸的美感。

颐和园玉带桥，摄影：王锐英

建造曲线桥梁应该有针对各个部位的严格的尺寸控制和比例变化的掌控，悬链线形式不仅是优美的曲线，也是非常便于实际放线、对准和检验尺寸的一种高效率的方法，可以说是测量技术与建造工艺的完美结合，因为这样不仅便于测量放线，保证石材放样和制作、施工安装的精度，还特别能够保证一座桥梁上四道栏杆尺寸的一致性，以及玉带桥和绣漪桥造型的一致性。想一想，这可是当年工匠们面对的一个艰难课题，放在今天也是不容易做到的！颐和园建造于乾隆十五年（1750年）前后，当时应该没有悬链线的数学知识吧，但不排除悬链线的应用，因为这很容易来自生活经验的总结。也有可能如同古建筑屋顶的举折做法，历史更为悠久，但计算和测量要比悬链线复杂。当然这只是笔者根据考察情况的一种验证和推测，还需要修建资料的佐证。

颐和园绣漪桥汉白玉栏杆中段呈现为悬链线形式

颐和园玉带桥栏杆曲线

颐和园绣漪桥中段栏杆地袱石曲线

有说玉带桥的桥面造型为反向曲线，但反向曲线可以由圆曲线、缓和曲线（一种曲率从零增加到某一参数的曲线）、抛物线等组成，只说反向曲线显然过于笼统，也没有可操作性。延伸介绍：我国古代桥梁总体上可分为梁桥、吊桥、浮桥、拱桥四大传统结构体系，其中拱桥的桥洞形式如同月亮，或似满月或似一弯新月，给人圆圆满满的视觉感受。确实，拱桥的拱券形式，又可简称其图案或图形绝大部分就是圆形的一部分。例如中国最早的石拱桥据历史记载是建于晋代（282年）洛阳旅人桥，北魏郦道元在《水经注》中记载该桥：“悉用大石，下圆以通水，可受大舫过也，奇制作”。早先还有人猜测桥拱如同满月般的一个大圆，连水下都有石造“拱券”，当然这种猜测是完全错误的。中国古人是很聪明的，不会笨到修建满圆的石拱桥，那样的话，一是力学上不合理、没必要，二是材料上、劳力上也是巨大浪费。那么石拱桥的拱券如果不是满圆，又都叫什么呢？

北京八里桥

浙江湖州潘公桥（引自《中国古桥学》）

参考图片

绝大大部分古代石拱桥采用的都是圆曲线，根据拱券取用圆弧长度（或接近圆曲线形式），一般将其分为多折边拱、半圆拱、马蹄形拱、椭圆拱、尖拱（锅底拱）、蛋圆拱、准悬链线拱等。半圆拱即半圆弧拱，如北京八里桥、浙江湖州潘公桥，取圆心角度数等于90度，即截取了圆的一半弧线构成拱券的形式，其矢高即等于半径，跨径即等于直径，矢高和跨径之比即矢跨比为1：2，等于0.5。若弧线长度超过半圆，即圆心角的度数大于180度，称为优弧，就是马蹄形拱，如绍兴的泾口桥。这种形式的桥梁很少见，但非常多见的是同样形式的月亮门，甚至还有不少是全圆弧的。也有桥下海墁石铺砌成倒拱形，与上面的拱桥相互呼应，其实不能称为倒拱桥，只是凹形桥底而已。

辽宁凌源明代天盛号桥（引自《中国古桥学》）

小于半圆弧为劣弧，但对于桥梁来说则是“优弧”，一般简称为圆弧拱，圆心角的度数小于90度，其矢高小于半径，跨径亦小于直径。如赵州桥跨径约37.02米，矢高才7.23米，矢跨比为0.195小于1/5，创造同类古桥的世界纪录。矢跨比越小说明桥拱的高度很小而跨度很大，这样使得桥梁很是平坦，故称为坦拱桥。

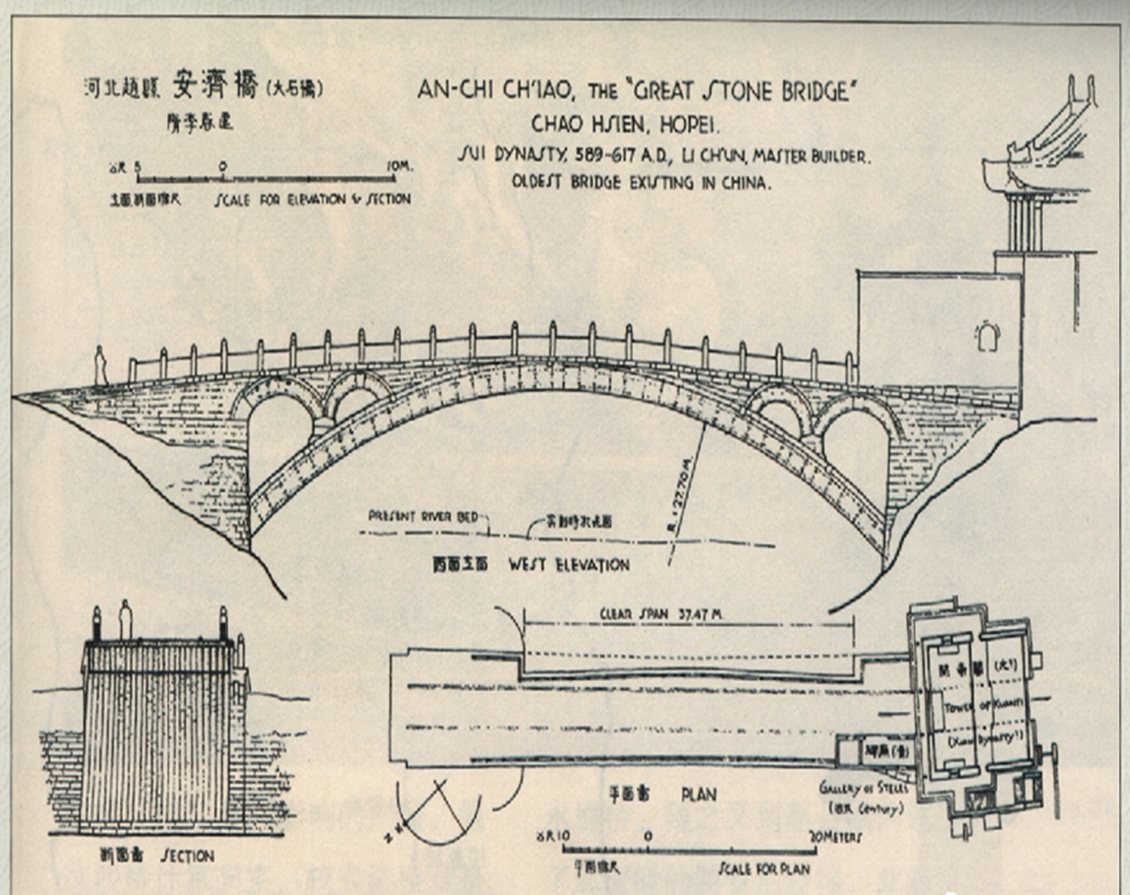
赵州桥拱券尺寸示意图采用局部的圆弧不仅单独使用，还有两向对称使用的，如颐和园的玉带桥、绣漪桥，还有石景山双泉寺万善桥等，就是两心圆曲线形式。如果呈中心对称的左右两段半径相等圆弧，其下分别垂直交于拱脚桥台，其上则相交于拱顶，形成双圆心尖拱券形式，圆弧在对称轴上交成尖角，此种形式又称为锅底券、尖拱桥。如果相交拱顶处再设置一小段圆弧，则为三心圆曲线，俗称蛋圆拱，如同立起来的鸡蛋外形。还有扁形的三心圆曲线拱桥。

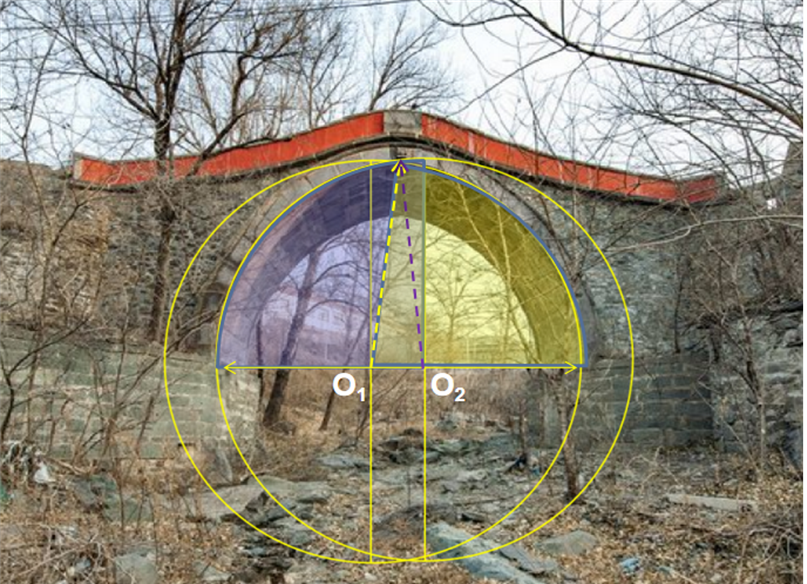
北京万善桥双心圆曲线尖拱桥

椭圆拱桥：苏州枫桥（引自《中国古桥学》）

回来说一说悬链线，这是现代拱式桥和悬索桥的一种构造形式。悬链线指的是两端固定的一条均匀、柔软的链条，在重力的作用下所具有的曲线形状。如果你拿住一条绳子的两端，让其中间自然下垂，所形成的曲线就是悬链线。然后将其上下反转，就构成了上拱如桥的形状，这样修建的拱桥就是悬链线拱。

悬链线示意和数学方程式（网络图片） 据说达芬奇研究过悬链线问题，伽利略还曾推测过悬链线是一条抛物线，其后几十年，许多数学家研究其数学性质，但没有得到准确结果。后来随着自然常数e和微积分方法的出现，直到1690年，持续一百多年的悬链线问题终于被惠更斯、莱布尼茨、约翰·伯努利解决，从而确定了悬链线的数学形式为“双曲余弦函数”，并不是抛物线。现今时代，微笑曲线盛行于世，但微笑曲线不一定是悬链线，也不一定是圆曲线和抛物线，因为微笑曲线形似人的嘴角上翘时的微笑形象，表达事物发展变化趋势的一种形态模拟。还有抛物线也在桥梁中有所应用，实际上抛物线和悬链线的形状差别并不大，对于能承受一定弯矩的刚性结构（如全部拱券为一个整体）来说，这种差别带来的影响很小。但是，对于零弯矩的柔性结构，拱轴线的形态尤为重要。尤其古桥均为离散的一块块石头相互叠压嵌挤而成，石块与石块之间是不能承受拉力的。如果同一界面出现有拉有压的情况就是出现了弯矩作用，但石块之间却又不能传递拉力，也就不能共同抵抗弯矩，导致偏心受压可能超出石块的边界，这样就会出现弯拉（偏心）破坏。倒置的悬链线则是承重和受力最好的拱券结构形式之一，在恒载（桥梁拱券和拱券以上的所有土石重量）作用下，拱券所承受的压力线很接近合理拱轴线，即截面受力均匀，弯矩很小（理想情况下，弯矩接近于零）。对于石拱桥来说，每块石头即不用很大，石块界面上接近全部受压，既可以节省材料，又充分发挥了石头承载压力的优越性。那么，在古代的桥梁中是否存在悬链线呢？在我国江南水乡的浙江绍兴，人们发现了迄今为止我国最古老的近似于悬链线拱的石拱桥—迎仙桥。该桥在明万历《新昌县志》中有载。还有位于嵊州市谷来镇谷来一村砩头自然村玉成桥始建于清道光十六年（1836），南北向横跨于东江之上，就是一座单孔悬链线型石拱桥，填补了我国桥梁史的空白。1992年5月5日，桥梁专家唐寰澄教授考察玉成桥时对此作了充分肯定。

浙江绍兴迎仙桥（引自《中国古桥学》）

浙江绍兴玉成桥（引自《中国古桥学》）

由此看来，我国的造桥不仅历史悠久，而且技术高超，古人们在很早以前便在桥梁建设中运用了悬链线。不过，古人并不知道悬链线这种数学曲线，他们只是从实践中反复摸索、总结出此类桥梁的建造技巧。大家在古桥中可能会发现很类似抛物线或悬链线的拱桥，其实大部分只是半圆拱或圆弧拱经过多年变形后的一种近似形态。当然也不能排除其原初的设计的可能性。如北京门头沟就有一座片石拱桥，看似象尖拱，也有可能接近悬链线。

门头沟片石拱桥，光绪十八年重修

来源: 北京建筑大学王锐英老师