我们每天看到海量的资讯，在这些纷繁复杂的信息中，如何做出准确的判断，如何避免被误导，如何保持独立的思考，这些能力都显得无比重要。

**数据驱动人生，数据决定一切。**也许你会说，我只相信我的眼睛！我只相信数据！真的是这样的吗？

你知不知道，数据也会说谎？

不说谎的数据也能欺骗人，这是真实的谎言。今天，我们一起来聊一聊统计学中的辛普森悖论。

什么是辛普森悖论？

如果我给你一组数据：一中的高考升学率为75%，二中的升学率为70%，你会把你的孩子送到哪个学校读书呢？

参加高考全部人数升学率

|| ||

当然是一中了！

对不起，也许你选错了！看一看下面这两张表。

理科高考升学率

|| ||

文科高考升学率

|| ||

虽然一中的总体升学率高于二中，但是不管是文科升学率还是理科升学率，一中都没有二中高！

不会吧？

揉揉眼睛再看一看。你没看错，数据就是这么神奇！

数据可不会是骗人的，不信可以自己动手验算一下，真的出现了这种违背常理的情况！

可能有些人还是一头雾水，虽然数据没错，可还是不能理解到底发生了什么，这个结论如此古怪！

难道数据有魔法？

这其实就是著名的辛普森悖论(Simpson's Paradox)：同一组数据，从整体和分组来看，得到的结果竟然截然相反！

辛普森悖论，是概率统计中的一种现象，在社会科学和医学科学统计中经常遇到，当人们尝试探究两种变量(比如新生录取率与性别)是否具有相关性的时候，会分别对之进行分组研究。然而，在分组比较中都占优势的一方，在总评中有时反而是失势的一方。该现象于 20 世纪初就有人讨论，但一直到 1951 年，辛普森在他发表的论文《The Interpretation of Interaction in Contingency Tables》(列联表中相互作用的解释)中阐述此现象后，该现象才算正式被描述解释。后来就以他的名字命名此悖论，即辛普森悖论，常被用来说明统计误用可能产生的误导性结果。

爱德华·辛普森(Edward Hugh Simpson, 1922-2019), 英国密码破译员、统计学家, 他因与乌德尼·尤尔(George Udny Yule, 1871-1951, 英国统计学家)一起描述辛普森悖论而知名。

爱德华·辛普森 (1942年)
为什么会发生辛普森悖论?

1.数据角度

辛普森悖论是指一种趋势出现在几组不同的数据中，但当这些不同组的数据组合在一起时趋势却消失或逆转的现象。

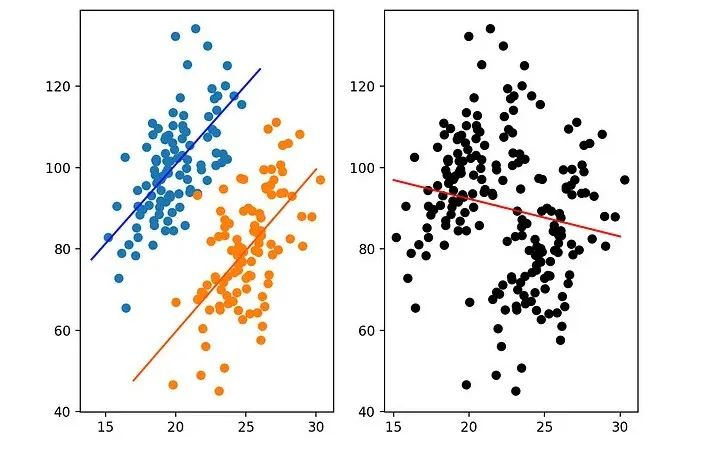
我们先从数据的角度来看，有两组模拟数据，它们都表现出 和 之间的正相关。在单独考虑每个组的情况下，两个组的最佳拟合线明显向上倾斜。但是，将这些组合并在一起时，最佳拟合线向下倾斜。可以用下面的图形来表示：

最佳拟合线是向上还是向下？辛普森悖论动态模拟图

辛普森悖论动态模拟上面的散点图，如果不拆分到子部分，单纯看 和 ，明显是负相关。但如果通过第三个维度颜色进行区分，发现 和 是正相关的。

辛普森悖论是数据分析领域中常见的现象，其数学表达式如下：

如果

那么，推不出

2.应用角度

从应用角度看，当我们对总体进行了第三个维度的拆分后，由于不同分析对象在第三维度的比例结构有差别，最终导致了悖论现象的发生。换句话说，如果两个分析对象，在所有的维度拆分上的比例结构都一致，那么也就不会出现辛普森悖论。

辛普森悖论最著名的例子之一来自一项关于加州大学伯克利分校研究生院招生性别偏见的研究。

在1975年发表在《Science》(科学)杂志上的一篇文章《Sex Bias in Graduate Admissions: Data From Berkeley》(研究生招生中的性别偏见：来自伯克利的数据)中，研究人员观察到加州大学伯克利分校男女录取率存在巨大差异。1973 年秋季的录取数字显示，申请的男性比女性更有可能被录取，而且差异如此之大，不太可能是偶然的。

|| ||

直观一看，很容易得出男生录取率比女生高的结论，怀疑招生中存在性别歧视也不无理由。

但结合申请院系信息，六大院系的数据如下：

|| ||

可以看到，上述6个院系中，女生在4个院系的录取率都大于男生，只有2个院系的录取率低于男生。加利福尼亚大学伯克利分校的统计学教授 Peter Bickel 后来发现，如果按照这样的分类，女生实际上比男生的录取率还高一点点，之前的结论被颠覆了。

从统计学家的观点来看，出现辛普森悖论的原因是这些数据中潜藏着一个魔鬼——潜在变量(lurking variable)。比如在上面这个例子里，女生更愿意申请英语系等，但是男生却更愿意申请工程学系等。

**另一个例子来自一项现实生活中的医学研究。**该研究比较了两种肾结石治疗的成功率。下表显示了大小肾结石治疗的成功率(这里的成功率实际上是指成功比例)和治疗次数，其中包括A开放式疗法、B封闭式疗法，表格中的数字表示成功案例的数量占该组总规模的比例。

|| ||

同理，在治疗小型和大型肾结石的两个分组里，A疗法的成功率都大于B疗法，但是计算总计时却是B疗法的成功率比较大。

为什么会出现这种情况？在分层统计的时候是一批人优秀，而到了总计的时候又是另外一批人优秀，完全相同的数据却得出相反的结论。

原因就是：每层之间的成功率差别很大。

用上面数据来说：治疗成功率中，小型肾结石的治疗成功率远大于大型肾结石，说明小型肾结石更好治，而人们使用A疗法做了更多大型肾结石(困难)的治疗，导致最终统计成功率时出现反转。

结语

通过本文对辛普森悖论的深入解析，有几点总结，供大家参考：

1. 辛普森悖论并不是悖论，只是个现象而已。只不过这个现象是反直觉的。但我们的直觉本身就不严格，没有经过任何数学层面的推导证明。这个直觉只是经常成立，而不是必然成立，如果数据特别一点，就不成立了。问题是：我们最初怎么会产生那个错误的直觉的？
2. 数据分析是用来做决策的，所以结论一定要慎重，数据分析能力除了靠专业知识技能打底，更要靠经验来烘托。
3. 数据分析中，遗漏了不该遗漏的维度，分析结论很有可能就是错误的，甚至是完全相反的。
4. 数据是一个有力的武器，它既能被用来澄清现实，也能被用来混淆是非；有人掌握了辛普森悖论，去帮助自己进行正确的数据分析，引导决策者进行正确的决策；也会有人利用自己所掌握的辛普森悖论，故意混淆视听，去蒙骗误导不懂统计学的决策者。