【译者之言:知道了太阳离我们的距离,那太阳有多重,或者更准确地说,太阳质量有多大呢?人类对它的认知,依然经历了一个漫长的过程。】

年轻的时候,我读过大量的诗歌。部分原因是学校让我们学习诗歌,而部分原因是因为我也不知道有什么更好的东西可读。正如我经常解释的那样,我移民来美国的父母对美国文学知之甚少,无法去指导我阅读,于是我见什么读什么。我因此阅读了大量通常小孩都应该比较讨厌的诗歌,因为也没有人告诉我,我应该讨厌诗歌。
在任何情况下,我都还记得那些日子里读过的很多诗歌,因为我总是很难忘记任何东西(除了重要的事情,比如我亲爱的妻子珍妮特为了让我永生,而给我的指示)。即使在今天,一些诗歌仍在为我的世界观增添色彩。
例如,有一首弗朗西斯·威廉·鲍迪伦(Francis William Baudylan)(不瞒你说,我不得不去查了一下他的名字)的诗,这是他写的一首短诗,诗的第一节是这样的:
黑夜有千只眼,
白天仅有一只;
太阳慢慢逝去,
光明渐渐枯萎。

无论是在文学上还是在科学上,在我读过的任何东西中,都没有遇到过像这四行诗那样坚定地赞赏太阳的重要性。
因此,年轻的时候,当我发现在我们普通世俗的历史上,我们所认识的第一个一神论者——埃及法老阿赫纳顿(Akhenaton)(公元前1372-1362年)——选择太阳作为唯一的最高的神,我一点都不感到惊讶。(是个不错的选择,阿赫纳顿,我觉得。很合乎逻辑。)
那么,我将继续讨论太阳。在上一篇短文中,我提出了一个问题:太阳有多远?答案是1.496亿公里(92.96百万英里),而太阳直径为139.4万公里(86.6万英里)。
现在让我们问第二个问题,而这次我故意用一种幼稚的方式:太阳有多重?
· · ·
一开始,西方宗教的传统观点是,太阳只是一个光的容器。
光本身是圣经中提到的,第一件被创造的东西,因为在第一天,“上帝说,你们要有光,于是便有了光。”(创世纪1:3)
首先,我们可以假设,光只是渗透到宇宙中,但是(还是在第一天),上帝将光明与黑暗分开,以区分白天和黑夜。
直到第四天,光才被收集到各种天体中,其中最亮的,无以伦比的是太阳,月亮远远跟在第二,星星只是一点点小光亮。“上帝造了两大团光;较大的一团管白天,而较小则管夜晚,他也创造了星星。”(创世纪1:16。)
地球上也存在光,它独立于天体。有短暂、偶尔出现的闪电,可能引发森林火灾。最终,人类点燃可能点燃了一些火,以产生光亮和温暖。对地球光源的研究提出了一个非常重要的观点,即光显然没有重量,它是非物质的。
由此,可以得出一个重要的结论。如果太阳只不过是一个光球,它也一定是非物质的,并且没有重量。如果是这样,即使它距离很远,很大,也没什么关系。无论它多大,它仍然是一个没有重量的东西,人们可能会说,它一定是绕着沉重的地球在转动。
对地球上光的第二个基本观察是,除非发出光的火焰持续得到燃料供给,否则它不可能长期存在。木材或油一旦消耗尽,任何光源都会消失。
另一方面,太阳不会熄灭,它一直发光,贯穿人类历史,没有变化,直到今天也没有显出逐渐减弱或衰退的迹象,更不用说熄灭了。也没有任何迹象表明,在这个过程中,太阳正在消耗燃料。
由此,可以得出结论,地球上的光与天上的光有一定的根本差别。地球上的光是基于燃料燃烧的短暂现象;而天上的光是永恒的,不需要燃料。这是一个表明地球上的自然法则不同于天上法则的重要例子。
希腊哲学家亚里斯多德(Aristotle)(公元前384-322年)相当详细地解释这个问题。一般来说,地球上的物体都是不完美的,是受时间限制的;腐烂和腐败是不可避免的。另一方面,天体是永恒的,是不会腐烂的;总之,就是完美的。地球上的物体,要么不移动,要么是通过向下下降或向上上升来移动。土地和水趋向于下沉;而空气和火会上升(按古希腊的观点,这是构成地球的四种基本物质或“元素”)。另一方面,天体一直在移动,但它们的移动既不是通过下降,也不是通过上升来完成的,而是在地球周围巨大、不变的圆环中前行。
既然如此,天体就不会是由土、水、空气或火构成的了,而是由完全不同的物质构成,这些物质被亚里斯多德称为“aither”,我们称之为“aether(以太)”或“ether(以太)”。它来自希腊语,意思是“燃烧发光”,因为天体永恒地发着光,而地上的物体是暗淡和黑暗的,除了偶尔有人点燃的火,但与以太的神火相比,人造的火就太不不完美了。
除非有支撑,否则岩石和重物体通常都会坠落。我们都知道这个道理。手握一块石头,伸手,放手,它自己会立刻落下。但为什么呢?
为了回答这个问题,亚里斯多德认为,每个物体在宇宙中都有一个自然位置,如果它在那个自然位置之外,只要没有被约束,它都会尽一切努力回到原来的位置。只要你把岩石保持在半空中,你就会感觉到它的重量,可以说就像它在挣扎,挣扎着想奔向宇宙的中心,这是固体物质的自然位置。如果你放手,它就会立即向那个中心移动;换句话说,它就会下落。
亚里斯多德似乎认为,一个物体的沉重与否,是衡量它渴望出现在其自然位置上的强烈程度的标准。因此,重的物体自然就会比轻得物体落得更快。一块岩石落下的速度就会比一片叶子快得多,而一片叶子又会比一根小羽毛掉得更快。
如果你愿意,你可以通过一个简单的实验,就可以证明亚里斯多德在这个观点中所犯的错误:
取两张同样的纸,让它们同时自由下落。它们两个都会下落得相当缓慢,速度相同。现在把一张纸揉成尽可能小的纸团,这一过程中其重量并没有改变,现在准备让两个物体自由下落,一个薄而平,一个揉成了紧凑的结构,但两者都有相同的重量。
让它们自由下落,看到了吧!揉成团的纸比重量相同的平纸下落要快得多。
为什么呢?因为在大气中下落的物质,必须把大气分子推开,这就吸收了下落的能量,使它们下落得较慢。如果是一个很重的物体,空气阻力带来的减缓可以忽略不计,但如果物体很轻,影响就会较大。如果物体既轻,与空气接触的表面又大,影响则会更大。
· · ·
在我们看来,这一切都是显而易见的,但直到亚里斯多德时代过去了19个世纪之后,意大利科学家伽利略(Galileo Galilei)(1564-1642年),才真正验证了古希腊关于下落物体的观念。
十六世纪九十年代,伽利略做了两件重要的事情。首先,他使用的物体比较重,空气阻力可以忽略不计。其次,他让物体在一个倾斜的平面上往下滚动,这降低和减缓了自然下落的趋势,这样他就可以更容易地观察和测量它们移动的速度。
他的实验证明了一个非常重要的事实——无论物体的重量如何,它们都以相同的速度下降。传说,伽利略同时从比萨倾斜塔的顶部扔下两个重球,来证明了这一点。一个的重量是另一个的十倍,一声闷响,它们同时砸在地上。几乎可以肯定的是,他并没有这样做,但他用球从倾斜平面滚下的实验,即使不那么壮观,也还是不错的。这推翻了亚里斯多德的物理学。

(在真空中,没有空气阻力,所有物体,无论重量多轻,表面积多大,都会以相同的速度落下。在真空中,羽毛会像炮弹落下一样快。这已经得到测试,确实如此。)
大约四分之三个世纪后,英国科学家艾萨克·牛顿(Isaac Newton)(1642-1727年)研究了伽利略和其它与运动物体有关的发现,并提出了三个假设,称为“运动三大定律”,令人满意地解释了地球上能遇到的所有运动类型。
运动第二定律规定,如果一个力施加在一个物体上,该物体就会经历一个加速过程。它会加速或减速,或改变运动的方向(这取决于施加力的方向)。更重要的是,同样程度的力施加在较重的物体上,会比施加在较轻的物体上产生更小的加速度。(要看到这一现象,可以先踢一个足球,然后用同样的方式踢一颗炮弹,看看会发生什么情况。)
牛顿定义了物质的固有特性,他称之为“质量”。特定物体的质量越大,施加给定的力,加速就越小。在地球表面,物体的质量与其重量成正比,但两者是不同的。重量在宇宙中随着位置发生变化,但质量不是——这一点我们现在不需要讨论。
从那时起,牛顿的运动定律就适用于所有的普通条件,它们已经被证明是一种完全令人满意的运动处理方式。(在极端条件下,爱因斯坦对这些定律的推广更为有用,但现在我们也不会讨论这个问题。)
用伽利略和牛顿的运动取代亚里斯多的的运动,这本身并不一定会改变自然法则在地球和天空上不同的命题。无论你如何解释物体落在地球上的方式,它们都是下落的;而天体不会下落,而是在做环绕运动。它们似乎在地球周围做环绕运动,但即使在前一篇短文中描述的日心说被大家接受,如果一些天体绕着太阳转动,它们仍然是在做环绕运动,不会落下。
现在怎么办呢?让我们换个办法吧。
· · ·
古希腊人认为行星作环绕运动, 不是因为行星的运动表明了这一点,而是因为圆圈被视为最简单和最完美的曲线。在他们眼中,天体只能是完美的。
由于行星的运动,并不像它们在其轨道(完美的圆)上应该有的那种运动,希腊人认为它们是以圆的组合在运动,是圆在圆上建立的结构,并且越来越复杂。他们坚持强行将行星的实际运动纳入他们的整洁和漂亮的概念。(他们称其为“保存外表”。)
正如上一篇短文中所描述的,当哥白尼认为,除了月球之外,行星实际上都是绕太阳转动的时候,他依然觉得它们是以圆的组合在运动。他也无法摆脱那个特殊的希腊想法。
打破这一魔咒的是德国天文学家约翰·开普勒(Johann Kepler)(1571-1630年)。他有一套由丹麦天文学家第谷·布拉赫(Tycho Brahe)(1546-1601年)记录的火星观测资料,这是那个时候编制得最好的资料,开普勒试图将这些位置与圆形轨道匹配,但未能成功。
绝望之下,他尝试了其他类型的曲线,并发现椭圆(一个稍微扁平的圆圈)正好与轨道匹配。他因此提出了“行星运动三大定律”,前两个定律在1609年提出,而第三定律在1619年提出。
第一定律规定行星轨道是一个椭圆。和圆一样,椭圆也有一个中心,但椭圆还有两个焦点,分别位于中心的两侧,而太阳则位于行星轨道椭圆的一个焦点上,而不是在中心处。
第二定律描述了一个给定行星的运动速度,如何随着离太阳距离的变化而变化。(太阳位于行星椭圆轨道的一个焦点,在行星沿着其轨道前行时,太阳和行星之间的距离也会发生变化。)
第三定律描述了不同行星绕太阳转动所需的时间长度,是如何与它们离太阳的距离有关的。
开普勒是第一个对太阳系进行本质描述的人,他的描述在今天和他自己的时代都一样缜密(牛顿和后来的爱因斯坦,进行了一些改进)。与开普勒给我们的画面相比,太阳系的画面不太可能再发生大幅改变。
然而,问题是,行星运动的三大定律与(地球运动)的三大定律有很大的不同,因此,即使到了17世纪中期,自然规则在地球和天空中,似乎仍然是不同的。
· · ·
1666年,艾萨克·牛顿(Isaac Newton)(1642-1727)离开了正在被瘟疫毁灭的伦敦,回到了他母亲的农场,一天晚上,他碰巧看到一个苹果从树上落下(不,它并没有砸中他的头),而此时月亮在天空中闪耀着光芒。

他想知道为什么苹果掉了,月亮却没有,然后他又想到,月亮是掉下来了,但它也在横向移动,两种运动的结合让它保持在绕地球的轨道上。从轨道的性质,我们可以计算出月球每秒钟朝地球落下的距离,它比苹果下落慢得多。当然,月亮比苹果距离远得多,也许地球的引力随着距离变大而下降。
我们知道,由于光的强度是距离的平方,地球引力的强度可能会以同样的方式下降。牛顿进行了计算,最终发现月球的下落速率只有实际的八分之七,这似乎推翻了他的理论,他失望地将其放弃了。
为什么他的计算失败了呢?首先,他使用的地球半径数字比实际的要小。这影响了他的计算。还有,地球的不同部分,可能会从稍微不同的方向,以稍微不同的距离吸引月球,而牛顿不确定如何去考虑这些情况。
然后有一天,在1684年,当英国科学家们正在讨论行星运动被太阳引力控制的可能性时,牛顿的朋友埃德蒙·哈雷(Edmund Halley)(1656-1742年)问他,如果太阳的吸引力随着距离的平方而下降,行星会怎样绕太阳转动。
“椭圆轨道,”牛顿说。
“你怎么知道呢?”哈雷说。
“我曾经计算过的呀,”牛顿说。
哈利非常兴奋,当他知道牛顿得出了错误的数字时,他坚持让牛顿再试一次。此时,牛顿已经发明了微积分学,这给了他进行此项计算正好需要的数学工具。另外,法国天文学家让·皮卡德(Jean Picard)(1620-1682年)在1671年发表了对地球半径新的估算,这比1666年牛顿所使用的更精确。
当牛顿回到他的计算中时,他可以看到就要得到正确结果了,但他不得不停下来恢复,因为兴奋让他中了风。
然后,哈利又残忍地催着牛顿写一本书,描述他的运动定律以及由此可以推断出的一切情况。哈利读了校样,并承担了出版费用(哈雷很富有)。这本书的短标题是《数学原理》,出版于1687年,这是世界上有史以来公认的最伟大的科学著作。
牛顿根据他的三大运动定律,制定了万有引力定律。他接着根据万有引力定律制定了行星运动的三大定律。
请注意,牛顿并非仅仅是提出了一个简单的引力定律。即使是原始人也知道所有的重物都会掉到地上。每个人都知道地球是引力的来源。这用不着牛顿告诉大家。
牛顿提出的是万有引力定律。宇宙中的每个拥有质量的粒子,会吸引其他每个拥有质量的粒子,吸引力与两者的质量成比例,而与两者之间距离的平方成反比。
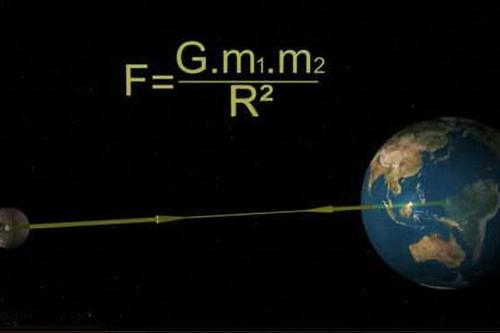
这就使得确定宇宙中不同物体的相对质量成为了可能。例如,月球不是简单地围绕地球转动。根据牛顿的定律,地球和月球都围绕一个共同的重心转动。这个重心位于连接地球中心和月球中心的直线上,它与地球中心和月球中心的距离与各自的质量成反比。重心可以加以定位,因为在地球绕它转动时,在一个月的过程内恒星似乎略有摆动。
地月系统的重心距离地球中心平均为4,728公里(2,938英里)。这实际上是在地球表面之下1650公里(1025英里),因此,说月球正在绕地球转动是非常合理的。
重心接近地球中心的距离比接近月球中心的距离要近81.3倍。这意味着地球质量是月球质量的81.3倍。我们无法用重心的位置来告诉我们任何一个物体的绝对质量,但我们可以得到两者的相对质量,这也就足够了。
· · ·
那么太阳的质量又如何呢?
我们知道月球绕地球运行的速度。如果月球离地球更远,它就必须经过更长的轨道,移动也会更慢,因为地球的引力影响会更弱。我们可以同时考虑这两种效应,计算出月球在任何距离上绕地-月系统的重心转动的速度,例如,在等于太阳与地球之间的距离上。
如果月球离地球1.496亿公里,并且附近没有其他天体干扰,它的移动确实就会非常慢,比地球在同样的距离绕太阳移动要慢得多。
为什么地球在太阳的影响下,比月球在同一距离上在地球的影响下,移动快得多呢?显然,因为太阳的引力比地球的引力要强得多。
为什么太阳的引力比地球的引力要强得多呢?因为太阳拥有更大的质量。根据牛顿万有引力定律,按照已知的月球和地球的轨道速度,以及已知的月球与地球之间的距离和地球与太阳之间的距离,我们就可以计算出太阳相对于地球的质量。
原来,太阳并不是非物质的光。太阳是一个质量等于地球质量33.3万倍的物体,在任何给定的距离上,太阳的引力都是地球引力强度的33.3万倍。
换句话说,一旦牛顿万有引力定律的结果被理解,就再也没有任何可能的理由(除了盲目和固执的信仰),来假设太阳绕着地球转动了。
1798年,英国科学家亨利·卡文迪什(Henry Cavendish)(1731-1810年)在实验室中测量了两个金属球之间的引力,并由此计算出了地球的实际质量。由此,我们可以得到月球和地球的绝对质量,但这些数字巨大得让我们无法想象。如果我们坚持使用相对质量,则会简单一些,假设月球质量为1,我们可以得到:
月球质量=1
地球质量=81
太阳质量=27000000
我们现在还知道太阳其它什么情况吗?是的,我们还知道太阳的直径等于地球的109倍(见上一篇短文),因此其体积等于地球的109×109×109,或1,295,000倍。
那么,如果太阳是由与地球完全相同的材料构成,它的质量应该等于地球的129.5万倍,但并非如此。
由于太阳的质量只有地球的333,000倍,因此它是由比地球轻的材料构成的。太阳的密度(每立方米千克数或每立方英尺磅数)为333, 000/1, 295, 000,只有地球密度的1/4。
现在我们可以得出一个伟大的结论。我们已经证明了月亮和太阳与地球一样拥有质量。通过类似的方法,我们也可以证明每一个物质天体都有质量,甚至是遥远的恒星和星系。(光和其他有些东西是非物质的,也没有普通意义上的质量,但我们可以忽略这一点。)
再就是,既然宇宙中所有带有质量的物体,似乎都按照牛顿的方程,遵守万有引力定律(除非极端情况下,我们必须使用爱因斯坦广义理论),那么,我们可能就会猜测,宇宙中所有物体,无论是在地球上,还是最遥远的星系,似乎都遵守相同的自然的法则——所有的自然法则,而不仅仅是万有引力定律。
当然,这仍然只是一个假设,因为我们不能在这么远的距离直接去测量宇宙,但是在牛顿伟大的著作出版三个世纪以来,我们确实还没有发现有任何东西,会导致我们,以任何严肃的方式,怀疑在地球上所确定的自然规律的普遍性。
然而,即便如此,仍然还是有牛顿方程式无法回答的问题。例如:
太阳有质量,但构成太阳的物质并不是构成地球的物质,因为构成太阳的物质只有构成地球物质密度的四分之一。
这是因为太阳比地球热得多吗?毕竟,密度确实会随着温度上升而下降。
还是因为太阳是由与地球相同的物质构成的,只是比例不同?地球上的一些物质也比其他物质的密度要小得多,也许太阳主要是由我们在地球上所知道的密度较低的物质构成的。
或者太阳是由不同于构成地球的物质构成的?即使它们都服从自然法则,也许天体的化学成分与地球根本就不同。也许每个天体都有自己的化学成分,没有两个是相似的。
如果是这样,我们又如何能知道呢?例如,我们又不能去往太阳,对它的材料进行取样,来进行分析。
事实上,法国哲学家奥古斯特·孔特(Auguste Comte)(1798年-1857年)在1835年指出,恒星的化学成分,就是那种永远无法获得的信息科学的一个示例。
不过,有时候这些“不可能!”的大嘴声明是危险的(尽管我自己也经常这样做)。在孔特去世仅两年,科学家们就学会了,如何获得这种孔特认为是永远都无法获得的科学信息。
在下一篇短文中,我们将谈论这是如何做到的,我们将会发现太阳是由什么构成的。
(作者:艾萨克.阿西莫夫(Isaac Asimov),译者:劲松)




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国