华罗庚先生讲过的一个故事

一个重要的军事秘密就这么被泄露了……

撰文 | 尹裕

1965年，华罗庚先生曾在一个中学做数学普及报告，讲了三个小时，内容极为丰富，非常生动，且都非常有价值。听众有一千多人，其中很多人对这个报告终生不忘。

下面是报告中说到的一个故事，是根据笔者的回忆整理的。

故事的开始是前苏联的第一次洲际导弹试射，目的地在太平洋里。在试射前，苏联官方向全世界发出一个公告，说明导弹可能落入的区域，警告所有过往船只绕道而行。公告给出了该区域的地图。图1是该区域的形状（草图）。

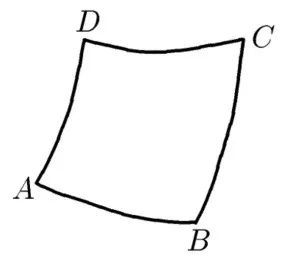
图1

用数学的语言说，这是一个“曲边四边形”。

这个区域为什么是这样的怪形状呢？这是华罗庚先生在这个报告中指出的一个问题。细心的人应该会想到这个问题，但未必能回答这个问题。下面的故事就越来越精彩了。

华罗庚先生解释说，首先要注意，地球是圆的，这个图是将一个球面图投影到平面上得到的，其实原图在球面上并不很“怪”。如果将这个曲边四边形恢复到球面上，就会看到曲边AB和CD都是大圆弧（也称“测地线”，在球面上连结两点的最短曲线就是大圆弧，相当于平面中的直线段），而曲边BC和AD是同心圆弧。

为了易于理解可以这样解释：设想大地是平面，那么这个区域就是如图2的曲边四边形ABCD，其中BC和AD是以O为圆心的圆弧，A在半径OB上，D在半径OC上，AB、CD为线段。

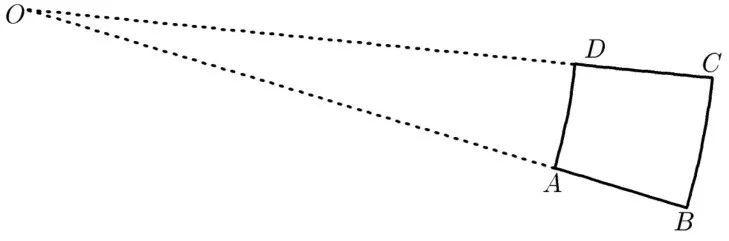
图2

这样就不难理解这个曲边四边形了。在图2中，O是导弹的发射点，导弹飞行的路程有一个偏差范围，可以控制导弹飞行的距离不远于OB，不近于OA，那么导弹的落点就位于以O为圆心OB为半径的圆内，同时又位于以O为圆心OA为半径的圆外，即位于两个圆所夹的圆环内；另一方面，导弹的飞行方向也有一个偏差范围，可以控制导弹的飞行方向位于∠BOC内。这样导弹的落点就位于上述圆环和∠BOC的公共部分，即曲边四边形ABCD内。

在球面上的情形与此类似，只是复杂些，需要将AB、CD换为大圆弧（BC和AD仍是以O为圆心的圆弧，但不在同一平面中）。发挥几何直观想象力不难明白。

讲明了这个道理，华罗庚先生进一步说，由此就可知大圆弧AB和CD的交点就是导弹的发射点，这样就可以从公告中的图出发计算导弹发射点。华罗庚先生计算的结果是，导弹发射点在乌拉尔山区。

不仅如此，由公告中的图还可以计算出导弹飞行距离的偏差范围，以及导弹飞行方向的偏差范围，都是关于导弹精确度的数据。

这些可都是重要的军事秘密！居然就这样破解了。在场的听众无一不被震撼。

笔者当年有幸听了这个报告，后来对这个故事的感想是：今后无论谁再试射导弹，在公告中恐怕再也不敢用这样的图了。

参考文献

[1]李克正:怎样学好数学.返朴(2019)

[2]尹裕:寻回美好的中学时代.数学通报2006年第1期