玩转十亿光年的超级铅笔

许多人在中学时代都练习过一项特殊技能——转笔！转笔玩家们也许并不知道：转笔游戏考验的是玩家如何心手相应地把握笔杆在转动过程中的角动量变化。殊不知，对于如何转笔这件“小”事，我们的宇宙才是超级玩家。

无处不在的角动量

在了解宇宙是如何玩转角动量之前，让我们先从不同的尺度上认识一下这位玩家。图中展示的是几个典型的天体尺度：从小到大依次是地球和月球组成的地月系统，尺度大约在40万千米；由太阳主导，行星、小行星及所属卫星等共同组成的太阳系，如果将奥尔特云也算在内的话，尺度约在一光年（即大约9.46×10¹²千米）；而太阳系只是银河系的普通一员，银河系由近2000亿颗恒星组成，尺度约在十万光年；数百乃至数千个星系聚集成为星系团，它们的尺度可以达到几百万光年。

天文学尺度从小到大：地月系统（约40万千米），太阳系（约一光年），银河系（约十万光年），星系团（百万光年），宇宙大尺度网络结构（数亿光年）▏素材来源：网络；图片制作：作者

根据现有的观测，这些不同尺度的系统都被宇宙“赋予”了角动量：月球自转的同时围绕地球公转，地球本身也有自转，地月系统和其他行星都围绕太阳公转，太阳则带领它的一群小迷弟小迷妹们围绕银河系中心做周期2.2亿年的公转运动，由星系组成的星系团也具有较慢的整体转动。由此可见，角动量是宇宙中各级结构的普遍属性。宇宙在各种尺度上玩转角动量，可以算作是超级玩家。

比星系团更大的尺度上，宇宙的物质分布呈现出网状结构，天文学家称之为宇宙网络结构（Cosmic Web），这些结构的大小甚至可达数亿光年。宇宙网络结构中最为壮观的应该算是纤维状结构（Filament），又称作细丝结构。顾名思义，细丝结构的特征是比较细长，像一支横卧在宇宙中的巨型“铅笔”。比如著名的斯隆长城（Sloan Great Wall），就是一条长达13.8亿光年的细丝结构。令研究人员感到好奇的是，既然宇宙在前四种尺度上都能得心应手地玩转角动量，那么在宇宙网络结构的尺度上是否也有惊人表现呢？

细丝结构的旋转

宇宙只是在各个尺度上默默地玩它的角动量，而研究人员为了证明其“王者”的地位忙得焦头烂额。

为了探究细丝本身是否转动，研究人员动用了著名的大样本巡天星系数据：斯隆数字巡天（Sloan Digital Sky Survey）。研究人员首先从斯隆数据库中提取了几百万个星系样本，利用一种叫做Bisous的识别算法从中寻找细丝结构。之后经过重重筛选，认定出了大约17800余根细丝结构以及组成它们的21万个星系。

接下来一个棘手的困难是：如何测量这些细丝结构的角动量？这是一次全新的尝试，通常的方法很可能行不通。研究人员经过大量的文献调研和多次的脑力风暴，最后从测量旋涡星系旋转的方法上获得了一些灵感：对于一个侧向（即盘面和视线方向平行）的旋涡星系，观测者可以利用多普勒效应测量盘两侧的恒星相对于整体的运动。盘面右侧的恒星远离观测者（向屏幕内运动），表现出谱线的红移；而盘面左侧的恒星靠近观察者（向屏幕外运动），表现出谱线的蓝移。综合来看，我们就能判断出整个星系在逆时针旋转。

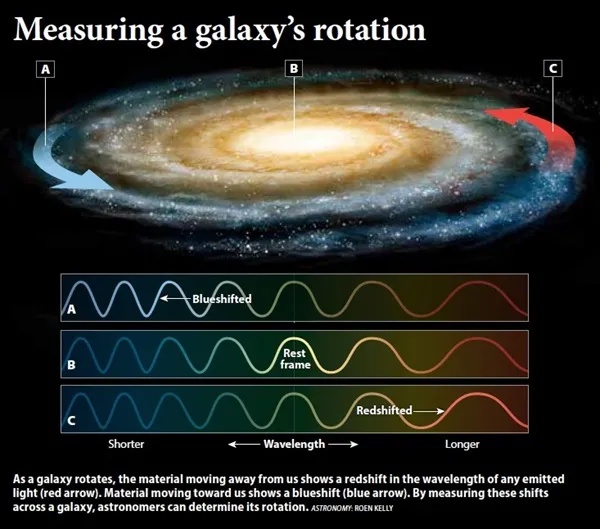侧向旋涡星系旋转的测量示意图。通过分别测量星系两侧恒星相对于星系整体的红移差，从而来判断星系的旋转。▏图源：https://astronomy.com

仿照这套方法，研究人员构建了细丝的旋转模型，在一根理想化的细丝中包含了6个星系，分别被划分在A和B两个区域（类似于旋涡星系的左右两侧）。如果能测量出A, B区域星系相对于细丝整体的运动差异——即一边远离另一边靠近，则表明细丝有旋转。需要提及的是，这里讨论的细丝是沿着轴向转动（箭头所示），而人们通常的转笔大多是沿着垂直于笔杆的方向转动。不过，正在进行的研究表明，细丝也有和转笔相同模式的转动。

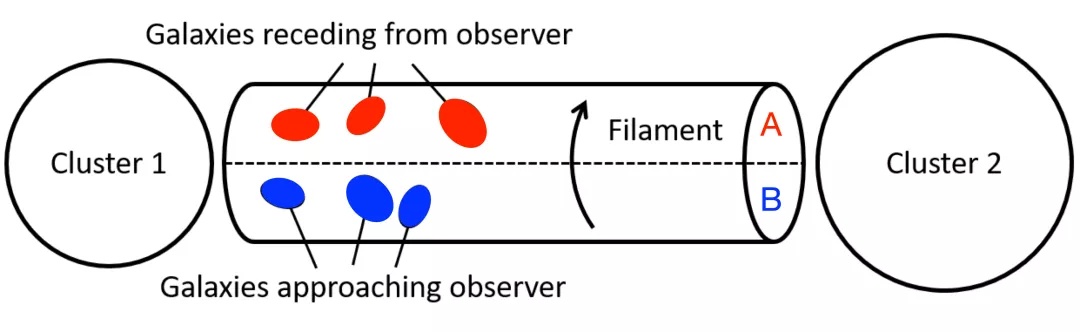
纤维结构旋转的示意图。圆柱体表示为理想状态下的纤维状结构，其中包含6个星系。▏图源 ：Roan Hagger/Abstrobites，作者修改。

许多物理过程都可以看作随机过程的组合，科学家的工作正是从纷乱的随机过程中抽丝剥茧，提取出内在的规律。测量细丝旋转这件事也是如此，通俗来说，测量得到的原始数据可能掺杂了许多的随机过程，难以提炼出真实可信的信号。这就需要研究人员做大量的随机测试，来验证信号偏离随机过程的程度。偏离越远，则表明测量的信号越真实可信。为此，研究人员采用了两种不同的随机测试方法，一种是让星系随机分布，另外一种是让细丝随机分布。借助于高性能计算机，研究人员对每一根细丝都进行了1万次随机模拟，模拟总数超过了十亿次。

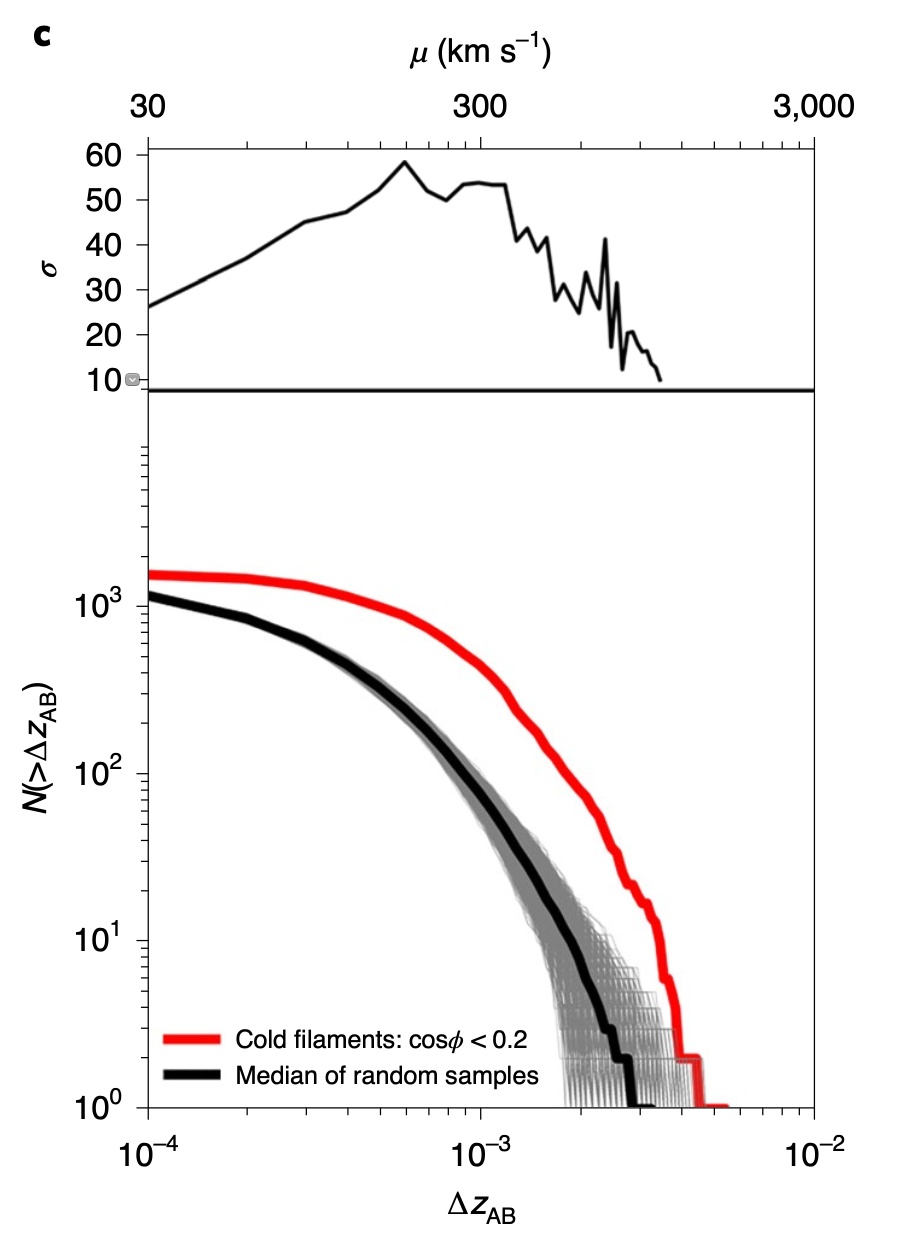
从观测中测量得到的细丝旋转信号（红色实线）与从随机模拟中得到的信号（灰色和黑色实线）的对比。横坐标表示细丝两侧中星系红移的差值，纵坐标表示累积数目。[1]

通过对比观测中得到的细丝旋转信号与从随机模拟中得到的信号，研究人员发现，对于所有细丝而言，真实观测中得到的信号是远远偏离（大约40σ）随机模拟信号的。这表明测量到的信号真实可靠。换句话说，宇宙把这17800根“超级铅笔”都转得“挺6”。

这激发起研究人员更大的好奇心：能否定量地研究单根细丝的旋转呢？

研究人员进一步分析了每根细丝的旋转信号，发现相对于随机模拟测试，有些细丝的信号强，有些信号弱。这取决于细丝本身的“温度”：温度越低，信号越强，温度越高，信号越弱。这里的“温度”刻画的是组成细丝的星系运动的混乱程度，“温度”越高，混乱程度也越高。

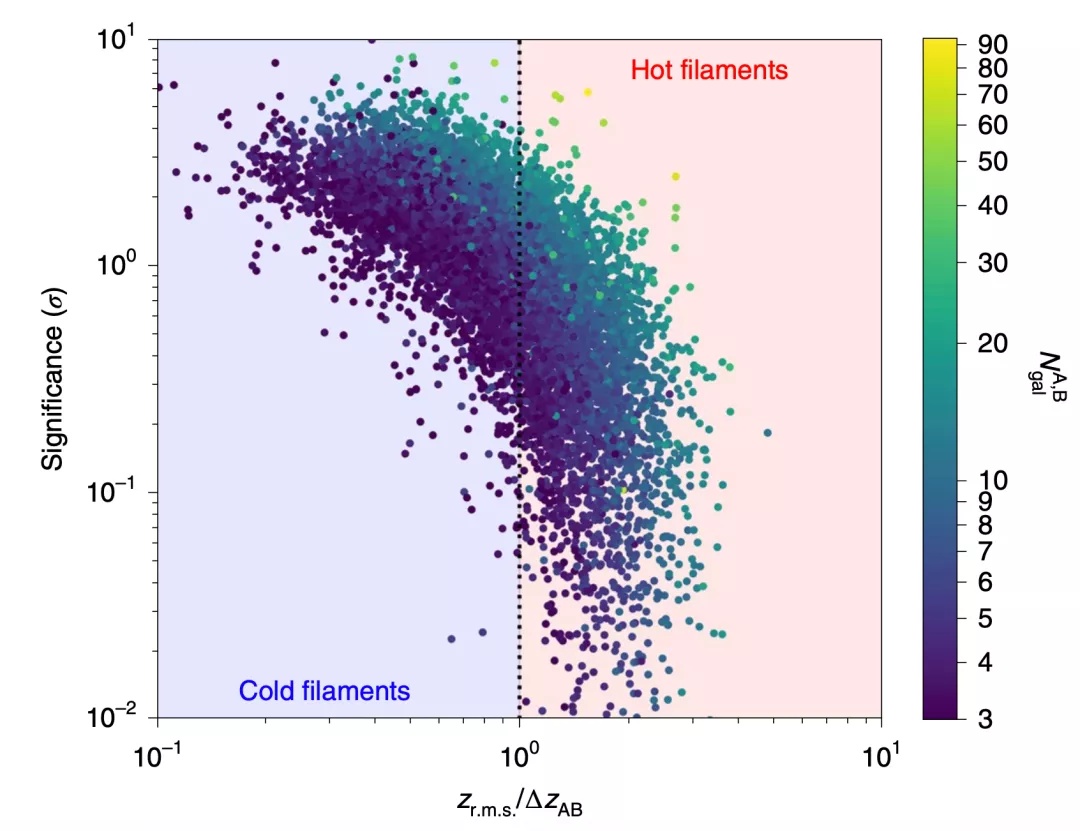
温度越低，细丝的旋转信号越强，温度越高，信号越弱。横坐标表示细丝的“温度”，纵坐标表示细丝转动的置信度。[1]

下图是本次工作最重要的一张图，它展示了所有17800多根细丝结构旋转曲线的叠加。其中，纵轴是细丝的转动速度，横轴是它们到细丝轴心的距离。可以非常明显的看出，曲线整体呈现出倒睡的“S”型。旋转速度从轴心处开始增加，到大约1 Mpc（约326万光年）处达到峰值，随后逐渐减少，在峰值约两倍的地方减少到0。这两个距离具体意味着什么，仍然有待进一步的科学研究。

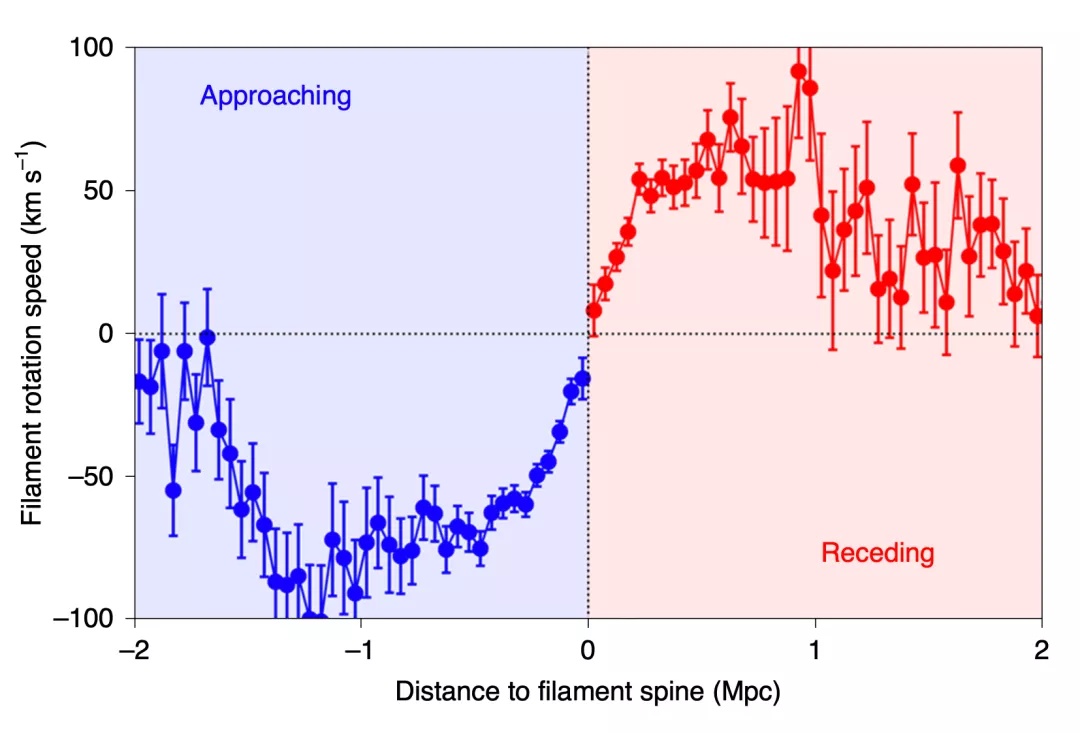
由一万七千多个细丝样本叠加得到的平均旋转曲线。细丝的一侧总是远离观测者，另一侧总是靠近观测者。[1]

宇宙为啥要“转笔”，什么时候开始转的？

根据现有理论，在宇宙的形成之初，所有物质均匀分布，像是一锅粥，几乎没有转动。因此，所有天体的转动只能在宇宙的各级结构形成中产生。各种尺度的天体如何获得角动量，一直是天文学上悬而未决的问题。在星系方面，一个比较流行的解释是潮汐扭矩理论（Tidal Tensor Theory），由著名的天体物理学家詹姆斯·皮布尔斯（James Peebles）、西蒙·怀特（Simon White）等提出。该理论的主要思想是，形成星系的物质在宇宙早期由于微小的不均匀性所导致的潮汐扭矩力，是星系开始转动的原因。

在宇宙大尺度结构的形成中，泽尔多维奇（Zel'Dovich）的近似理论描绘了一幅宇宙网络结构形成的直观图像：一团物质的分布中微小的不均匀性会引发物质在万有引力作用下的塌缩。总有一个方向最先完成塌缩，这使得扰动区域内的物质被摊成一张“薄饼”。随后，“薄饼”面上的某个方向完成了塌缩形成细丝结构。最后，细丝结构也完成塌缩，形成前文提到的星系团。研究人员据此猜测，细丝也许是在“薄饼”塌缩的过程中转动起来的。

需要说明的是，上述的三个塌缩过程并非依次进行，而是同时发生，只不过快慢不同。因此，细丝的两端一般会与一个或者两个星系团相接。研究人员比较了不同细丝两端的星系团质量发现，连接较大质量星系团的细丝旋转信号也更强，猜测其原因可能是大质量的星系团对细丝具有更强的潮汐扭矩作用。

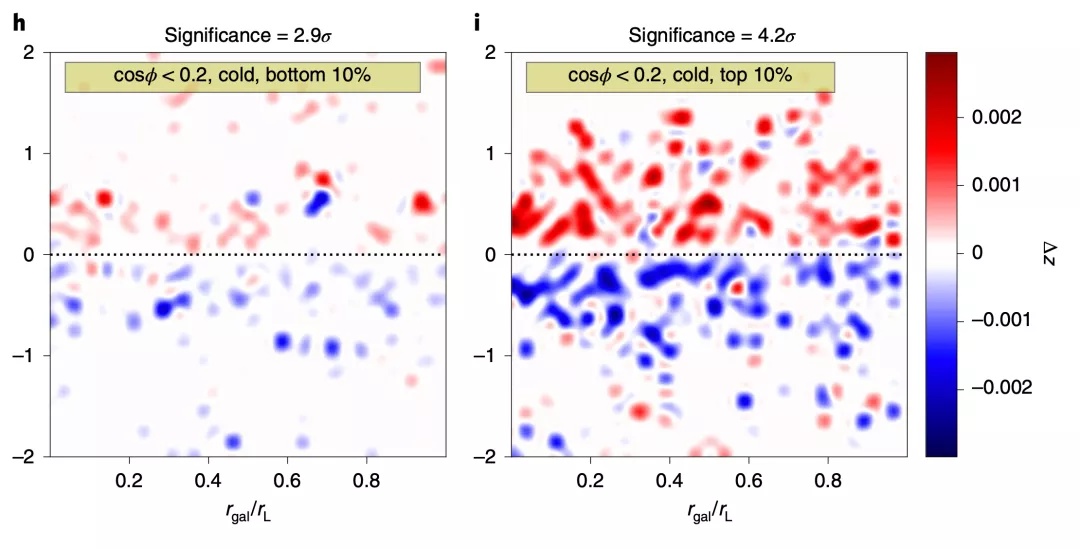
细丝两端的星系团质量对细丝旋转信号的影响：左图是连接小质量星系团的细丝信号，置信度较低；右图是连接大质量星系团的细丝信号，置信度较高。[1]

由星系组成的细丝结构，可以看作是星系通往星系团的“高速公路”，深刻地影响着星系的形成和演化。解开细丝转动的奥秘，不仅能帮助人们认识和理解这些宇宙中最大尺度的结构是如何形成与演化的，同时，也对星系形成的研究有启发作用。

终有一天，我们将揭开“宇宙转笔”的神秘面纱。

参考文献：

1. Wang, P., Libeskind, N. I., Tempel, E., Kang, X., and Guo, Q., “Possible observational evidence for cosmic filament spin”,Nature Astronomy, 2021. doi:10.1038/s41550-021-01380-6.

2. Tempel, E., Stoica, R. S., Kipper, R., and Saar, E., “Bisous model-Detecting filamentary patterns in point processes”, Astronomy and Computing, vol. 16, pp. 17–25, 2016. doi:10.1016/j.ascom.2016.03.004.

3. Tempel, E., Tuvikene, T., Kipper, R., and Libeskind, N. I., “Merging groups and clusters of galaxies from the SDSS data. The catalogue of groups and potentially merging systems”, Astronomy and Astrophysics, vol. 602, 2017. doi:10.1051/0004-6361/201730499.

封面图源：

AIP/ A. Khalatyan/ J. Fohlmeister

作者简介

王 鹏

天文学博士，毕业于中国科学院紫金山天文台，现于德国波茨坦天文物理研究所从事博士后研究。研究方向为宇宙大尺度结构和星系形成。

校对：陈厚尊

轮值主编：张旸

制作、编辑：王科超