汉朝人怎样解方程组？-

我们看看汉朝数学家怎样解方程组：

“今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗。问上、中、下禾实一秉各几何？”（图3-2）

这道题出自古代中国著名的数学典籍《九章算术》，成书于汉朝。禾是稻子，秉是“捆”“束”的意思，将上述文言翻成大白话，意思是这样的：

优质稻子3 捆，普通稻子2 捆，劣质稻子1 捆，能碾39 斗米；

优质稻子2 捆，普通稻子3 捆，劣质稻子1 捆，能碾34 斗米；

优质稻子1 捆，普通稻子2 捆，劣质稻子3 捆，能碾26 斗米。

如果有优质稻子、普通稻子、劣质稻子各1 捆，各能碾多少米呢？

让初中生解这道题，会用x、y、z 分别代表优质稻子、普通稻子、劣质稻子各1 捆所能碾出的稻米，然后列方程组如下：

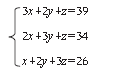
这个方程组怎么解呢？需要逐个消元，各方程左右项分别乘以某个常数：

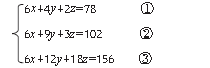
拿②减①，得到④ 5y+z=24。拿③减②，得到⑥：3y+15z=54。将5y+z=24 的左右项各乘以15，得到⑦：75y+15z=360。

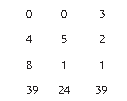
拿⑦减⑥，得到 72y=306，求出 y=4.25。再将 y 的值代入 5y+z=24，求出 z=2.75。最后将 z 和 y 的值代入 x+2y+3z=26，求出 x=9.25。 x、y、z 分别是 9.25、4.25、2.75，说明 1 捆优质稻子能碾 9.25 斗米，1 捆普通稻子能碾 4.25 斗米，1 捆劣质稻子能碾 2.75 斗米。汉朝数学家解方程组，也要逐个消元，但是过程特别麻烦。他们必须用算筹在地上摆出一个矩阵，该矩阵可用阿拉伯数字表示如下：

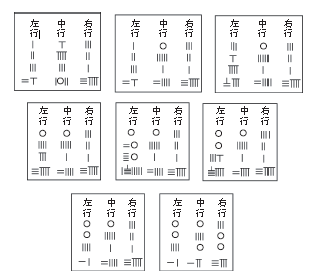
右边那列 3、2、1、39，表示 3 捆优质稻子、2 捆普通稻子、1 捆劣质稻子能碾 39 斗米，相当于方程 3x+2y+z=39。中间那列 2、3、1、34，表示 2 捆优质稻子、3 捆普通稻子、1 捆劣质稻子能碾 34 斗米，相当于方程 2x+3y+z=34。左边那列 1、2、3、26，表示 1 捆优质稻子、2 捆普通稻子、3 捆劣质稻子能碾 26 斗米，相当于方程 x+2y+3z=26。汉朝数学家通过变换矩阵来消元。《九章算术》里记载的第一步变换是“以右行上禾，遍乘中行”，也就是用右列第一项的数字 3，去乘中间那列的每一项。乘过以后，原始矩阵变换如下：

然后让中列每一项减去右列对应项的某个常数倍（这里取 2 倍），矩阵变换成：

然后“又乘其次，亦以直除”，将左边那列也乘以某个常数（这里乘以3），让左列减右列，得到：

然后“以中行中禾不尽者遍乘左行，而以直除”，让左列乘以中列未消去的中间项5，再减去中列各项的某个常数倍（这里取4 倍），得到：

经过以上四步变换，左列数字出现了两个零，相当于消去了两个未知数，只剩下36 和99，相当于36z=99。99 除以36，得到z=2.75。

沿用前面的变换方法继续消元，并代入求解，得到x=9.25，y=4.25，方程组被完整求解。

汉朝还没有小数，汉朝数学家只能用分数来表示小数。在《九章算术》里，这道题的答案是“上禾一秉，九斗四分斗之一；中禾一秉，四斗四分斗之一；下禾一秉，二斗四分斗之三”。用现代话讲，优质稻子每捆碾米九又四分之一斗，普通稻子每捆碾米四又四分之一斗，劣质稻子每捆碾米二又四分之三斗。

将方程组写成矩阵的形式，再用矩阵变换来消元，最后求得方程组的解，这是汉朝数学家求解方程组的方法，也是过去两千年间古代中国绝大多数数学家求解方程组的经典方法（图3-3）。现代高中生或者大学低年级学生学习线性代数时，遇到比较复杂的方程组，也要把方程组转化成矩阵，再用矩阵变换来消元。由此可见，古代中国数学家用矩阵求解方程组的方法实在是非常经典。