趣谈无理数e(十七) 掀开蒙在上帝公式e^(πi) ➕1=0头上的神秘面纱

高俊科趣谈无理数e(十七)

十七 掀开蒙在上帝公式e^(πi) ＋1=0头上的神秘面纱

不少书中都讲到复数域中的欧拉公式，如以色列人的著作《一个常数的传奇》、日本人的著作《数学与生活》、中国人的著作《不可思议的e》等数学书中都讲了欧拉公式e^(πi) ＋1=0，这个公式把五个最特殊的数0、1、i、π、e连在一起，让它们共处于等式e^(iπ) ＋1=0中。以色列人伊莱.马奥尔在其著作《一个常数的传奇》中评论说，“很多人认为它具有不亚于神的力量”，美国数学家本杰明..皮尔斯说”这个公式是绝对正确的，也是绝对诡异的，我们能够证明它，但不能理解它”。由此这公式也被称为上帝公式。

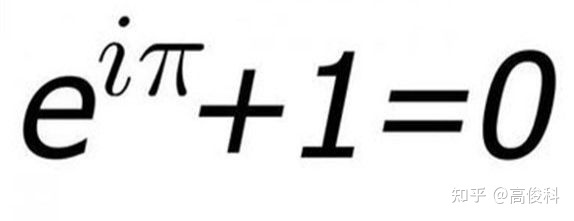在实数域中，对于余弦函数cost，通过图示我们能观察得出cosπ=–1，这就有cosπ ＋1=0，这就是余弦函数把三个特殊的数0、1、π共处一式了，没有谁会感觉到这样让0，1，π共处一个等式cosπ ＋1=0神秘，也不会想到再用什么其它方法证明cosπ ＋1=0这一恒等式。

在复数域中，对于欧拉恒等式e^(iπ)＋ 1=0也应该是一样的。

在复数域中，对于指数函数e^(it)，通过图示我们能直接得e^(iπ)=–1 ，这就有e^(iπ) ＋1=0，这就是指数函数e^(it)把五个特殊的数0、1、i、π、e共处一式e^(iπ) ＋1=0了，这就不需要再用什么其它方法进行证明。

接下来我们来看对于指数函数z(t)=e^(it)怎么看到e^(iπ)=–1.

在复平面上，函数z(t)=e^(it)随t变化的轨迹是一条曲线，z(t)=e^(it)的导数是dz(t)/dt=ie^(it)=iz(t), 在曲线上任何一点，iz(t)表达的是动点z(t)的运动方向与矢径本身z(t)总保持反时针方向垂直，所以z(t)轨迹是一个圆。因为z(0)=1，所以z(t)的轨迹是一单位圆 。

dz(t)/dt的方向是z(t)的运动方 向，绝对值Idz(t)/dtI是动点z(t)的线速度，Idz(t)/dtI=1，在单位圆上，z(t)路径的长度与经过这路径时t的数量恒相等，t从0变化到π，z(t)在单位圆上的路径，或说弧长也就是π，在单位圆上从z(0)=1反时针方向经过弧长π，就是-1，即z(π)=e^(iπ)=-1，这就得到了复平面上的欧拉公式

e^(iπ) ＋1=0

这就让数字0、1、i.π、e共处于一个等式中了，这所谓上帝公式没有一点神秘之处,这就揭下了披在这上帝公式头上的神秘面纱？

在单位圆上，z(t)路径的长度与经过这路径时t恒相等，单位圆上弧与其所对的角度数(弧度)总相等，所以，z(t)=e^(it) 中t也就恒等于这动点z(t)转过的角度。

如果自变量t从0开始有改变量x，则x也是动点z(t)=e^(it) 转过的角度数，对应的终点就是cosx ＋isinx 即 z(x)=e^(ix) 与cosx＋ isinx是复平面上的同一个点 ，因此，恒有

e^(ix)=cosx＋ isinx

成立。