高俊科趣谈无理数e(一)一 怎么理解年增长率概念

高俊科趣谈无理数e(一)

一 怎么理解年增长率概念

1 为什么提出这个话题?

年增长率概念很简单，这概念是中小学生、大学生都理解的概念，是人们日常生活中经常使用的概念，也是人民日报上经常出现的概念，这概念很基础。

这里提这问题是不是太简单了?实则不然。看我们不少大学教材把这概念理解错了，深刻理解这概念就能看清楚这些大学教材中是怎么错的?

先看看这40年前大学微积分中的习题19怎么解答?10年前的微积分教材中的例题8解答的对不对?

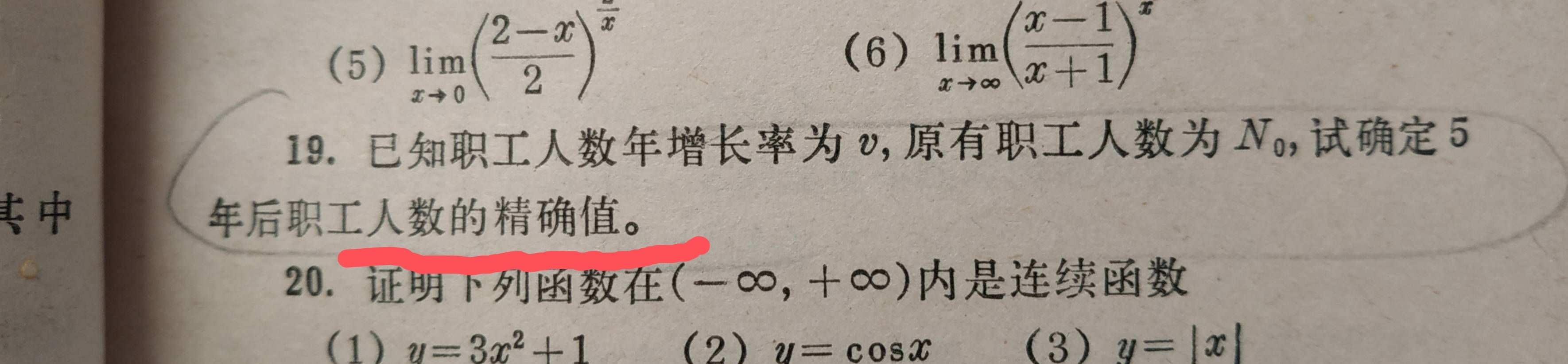
本篇将对这习题和例题具体分析。

大学数学教材中至今还有类似的问题，在金融学、工程经济学、公司理财中这类问题就更多了。

正确理解年增长概念就不会出这大学教材中的错误了。

2 怎么理解年增长率概念?

我们都知道年增长率就是

(年末值 -年初值)/年初值

例1 一棵树高1米，一年长成2米，这树年长高

(2 -1)/1=100%；反过来，树高1米，一年长高100%，一年后的树高就是2米。这是没有任何歧义的。

我们能不能说，一年长高100%，半年就长高50%，半年后树高1.5米，下半年在1.5米的基础上再长高50%，成1.5(1 50%)=2.25米，因为半年计算一次，半年计算一次比一年末计算得到的值精确?认为2.25米比2米更精确一点?

一定不能吧，进一步，能不能说每月计算一次，一年中计算12次，得出一年后的树高是1x(1 100%/12)^12=2.613米就更精确?

这习题19就陷入了这思维。

这树一年长高的比率100%是一年中的增长情况，体现的已经是一年生长的结果了。

例2 张家年初有资产100万元，年增长率是10%，求张家一年后的资产是多少?

这题很简单，张家一年后的总资产就是110万元。

这年增长率本身体现的是一年的最终结果，这结果包括一年中前半年资产减少后半年增加，一年中有10个月资产增加有2个月资产下降，一年中资产“每时每刻”都在增加等等各种情况，解答这题不需要对一年中各个时段资产增加的情况进行区分。

这例题8的解答是不是陷入误区?

这例题8的解答确实错了。对例题8有一种错误理解是，例8中的“年增长率”概念不是我们在中小学理解的概念，这里是瞬时增长率概念。

这辩解是说不通的，理由有三：一是这些教材中都没有给出“年增长率”别的含义；二是这些题都是在同本教材中讲导数，即讲”瞬时变化”概念之前的数列极限部分，这里还是不能涉及到瞬时变化的；三是对这题中的“年增长率”概念理解成瞬时概念，在极限一节解答这题的起步点也就不成立了。

再看这下边这例题14讲化学反应计算讲的对不对？这例题取自1995年的一本工科生用的微积分教材。

总之，这些大学数学教材把这个问题理解错了。

还有其它一些教材也存在这类错误，这错误思维不是一两本教材中疏忽发生的，如果仅出现在一两本教材中就没有在这里讨论的必要了，这错误不是凭空产生的，我们将一步步分析。