流体粘度极限，如何用量子力学解释？

尽管液体的粘滞性强烈地依赖于温度和压强，但是其极小值却被基本物理常数所限定。

撰文 | Kostya Trachenko（英国伦敦女王玛丽大学教授）Vadim V. Brazhkin（莫斯科高压物理研究所所长）

翻译 | 严佳

校译 | 张一

上世纪70年代，诺贝尔奖得主、物理学家普赛尔（Edward Purcell）注意到，不存在比水的粘度低得多的流体。在短文《低雷诺数下的生命》（Life at low Reynolds number）的首段，他写道：“粘度的跨度很大，但却都截止在同一个地方。令我不解。”

普赛尔所说的“截止在某个地方”，是指流体粘度不会低于某个特定值。他在短文的第一个脚注中指出，韦斯科夫（Victor Weisskopf）曾向他解释过这个现象。然而，迄今为止，还没有人见过这个解释的公开发表记录。即便如此，在普赛尔文章发表前后，韦斯科夫自己也发表了题为《关于液体》（About liquids）的短文。它以一个发人深省的故事开始，讲述了理论物理学家在试图仅用量子力学推导物质状态时面临的挑战。他们可以预测气体和固体的存在，却无法预测流体。

要点在于流体难于对付——这在教科书中讲的十分透彻。例如，朗道（Lev Landau）和栗弗席兹（Evgeny Lifshitz）的《统计物理学》（Statistical Physics）中一再强调，流体的热力学性质和温度依赖性根本无法以适用于所有流体的解析形式计算出来。原因在于很强的分子间相互作用以及缺乏简化固体理论的小振动。这种复杂性体现在著名的“无小参数”问题上：流体既没有气体的弱相互作用，也没有固体的小的原子位移。尽管面临这样的困难，我们还是根据流体激发发展了流体的热力学理论，它目前正在经受细致的检验。

粘度极小值

同时，我们可以向理论家提出这样的问题：他们是否充分理解了粘度，从而回答普赛尔的问题，为什么所有的粘度系数都截止于同一位置。粘度系数η表示流体抵抗剪切力的能力，决定着诸如扩散和耗散等重要性质。在稀薄的类气体流体中，η由平均自由程L以内运动的分子及碰撞中的动量传递所决定：具体而言，η=ρvL/3，其中ρ和v分别为分子的密度和平均速度。

粘度在高温下增大，在低温下减少，意味着它有一个极小值。该极小值产生于两种不同的粘度区域间的平滑过渡（crossover）：一个是气体类区域，温度较高的粒子的动能提供了较大的动量传递，因此导致较大的η；另一种是液体类区域，温度较低的粒子跳动频率降低，液体流动速度减慢，也导致较大的η。

看一下临界点以上的过渡很方便，它在那很光滑，且没有气液相变的干扰。借助描述流体流动性质的运动粘度ν=η/ρ来考虑。下页（原文第67页）的图显示了几种超临界流体 （supercritical fluids）的实验数值。运动粘度显然存在极小值，可以把它们理解为气体类和流体类行为之间的过渡状态。

粘度极小值为普赛尔问题提供了第一条线索。当粘度达到其极小值时，它们当然就会停止下降。但是每个极小值本身是否可以任意地接近零？（注意，我们不在这篇快速研究中讨论超流。）为什么η的极小值很难向上或向下移动，且在某种程度上接近于环境条件下的水的粘度？

如果科学家们能够计算出粘度的极小值，就可以回答这个问题。但正如朗道和栗弗席兹在他们的书中讨论的那样，这很复杂。分子间相互作用很强，而且是依赖系统的。只使用理论且没有模型输入，即使是简单流体计算粘度参数也很困难。而对分子流体，如水，这近乎不可能。

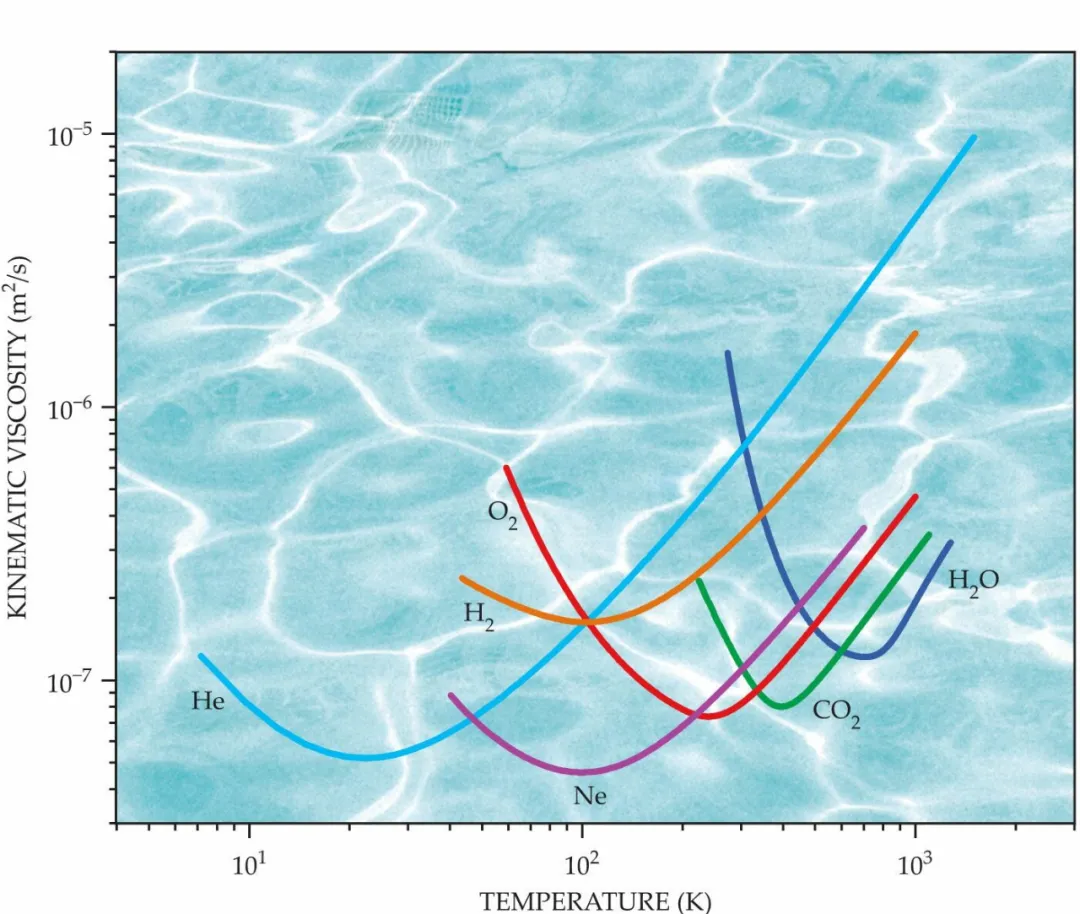
惰性分子流体的实验运动粘度。每种流体都表现出一个极小值。氦、氢、氧、氖、二氧化碳和水的粘度分别在20兆帕、50兆帕、30兆帕、50兆帕、30兆帕和100兆帕时绘制。(来源：NIST，https://webbook.nist.gov /chemistry/fluid)

一个具有启发性的近似

基本常数和水

基本常数在更高层次上对生命亦友好。生物过程，如细胞中的进程，在很大程度上依赖水。例如，如果普朗克常数取不同的数值，水的粘度也会发生变化——它的运动粘度ν，与水的流动有关，它的动力学粘度η，决定其内部摩擦和扩散。如果粘度极小值因ħ的数值较高而增加，水将变得更加粘稠，生物进程也将不同。生命可能不会以其目前的形式存在，甚至根本不存在。

人们可能希望细胞仍然可以在这样的宇宙中生存，通过找到一个更热的地方，使过度粘稠的水变得稀薄。但这也于事无补。普朗克常数设定了一个粘度不能继续降低的、无关温度的极小值。水和生命确实和物理世界的量子化琴瑟和谐。

我们希望普赛尔会对他的问题的答案感到高兴。除非他在上世纪70年代已经从韦斯科夫那里听到了这个答案。

参考资料

‣ E. M. Purcell, “Life at low Reynolds number,” Am. J. Phys. 45, 3 (1977).

‣ V. F. Weisskopf, “About liquids,” Trans. N. Y. Acad. Sci. 38, 202 (1977).

‣ L. D. Landau, E. M. Lifshitz, Statisticheskaia fizica (Statistical Physics), 2nd ed., Pergamon Press (1969).

‣ J. E. Proctor, “Modeling of liquid internal energy and heat capacity over a wide pressure– temperature range from first principles,” Phys. Fluids 32, 107105 (2020).

‣ K. Trachenko, V. V. Brazhkin, “Minimal quantum viscosity from fundamental physical constants,” Sci. Adv. 6, eaba3747 (2020).

‣ J. D. Barrow, The Constants of Nature: From Alpha to Omega— The Numbers That Encode the Deepest Secrets of the Universe, Pantheon Books (2003).

本文经美国物理学会（AIP）授权翻译发表于《返朴》（FanPu），原文译自Kostya Trachenko and Vadim V. Brazhkin , "The quantum mechanics of viscosity", Physics Today 74, 66-67 (2021) https://doi.org/10.1063/PT.3.4908

Reproduced from [Kostya Trachenko and Vadim V. Brazhkin , "The quantum mechanics of viscosity", Physics Today 74, 66-67 (2021) https://doi.org/10.1063/PT.3.4908], with the permission of the American Institute of Physics.

转载请保留以上版权声明。

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。