剪刀下的莫比乌斯带

　　剪刀下的莫比乌斯带

　　“莫比乌斯带”这个词，大家一定不陌生——将一根纸带扭转180度后两头再粘连起来，形成的纸带圈就叫做莫比乌斯带。

　　莫比乌斯最初于1858年，由德国数学家奥古斯特·莫比乌斯和约翰·利斯汀独立发现。与环形曲面不同的是，莫比乌斯带只有一条边和一个面，因此用它制作的传送带，磨损更加均匀，使用寿命更长。莫比乌斯带也被用来制作针式打印机的色带，从而可以节约材料。奥运奖牌、工作牌的带子设计成莫比乌斯带，奖牌就能服帖地平置于胸前。利用莫比乌斯带制成的磁带可以使播放时间增加一倍，而且不用翻面。无感电阻、莫比乌斯共振器等电子器件也是利用了其性质。至今，莫比乌斯带已经被广泛应用在雕塑﹑绘画﹑邮票﹑建筑﹑音乐﹑电影﹑文学﹑游戏等许多领域。

　　在数学上，莫比乌斯带没有正面与反面之分，属于不可定向曲面的一种。它为现代几何分支——拓扑学的发展起了重要作用。事实上，莫比乌斯带本身就有着很多神奇的性质。

　　一﹑n等分莫比乌斯带

　　想一想，如果我们将莫比乌斯带的宽度2等分，然后从中剪开，结果会变成两根纸带吗？答案可能与大多数人的直觉大相径庭——是一根绕了4个半圈的纸带。

　　那么，如果把莫比乌斯带n等分，会得到什么呢？

　　为了叙述方便，下面把绕了k（k≥0）个半圈的纸带记为Mk。特别的，M1就是莫比乌斯带，而M0则是纸环。

　　实验发现：

　　若n=2，结果是1个M4；若n=3，结果是1个M4，1个M1；

　　若n=4，结果是2个M4；若n=5，结果是2个M4，1个M1；

　　不难发现：n每增加2，结果就比之前多1个M4。

　　这一规律对任意的n是否都成立呢？

　　其实不难理解，答案是肯定的。分成的份数每增加2，可以理解为先沿着边缘剪了一刀，即相当于把纸带三等分。因此最后会增加1个M4。

　　这里给读者留个问题，用将n张相同的纸条叠在一起，一端扭转180°之后，把这n组端头依次用胶水粘在一起，制作一个“n层的莫比乌斯带”，其结构与n等分莫比乌斯带的结果拓扑等价吗？为什么呢？

　　二、2等分绕了k个半圈的纸带

　　在n等分莫比乌斯带（M1）之后，我们会很自然的想到n等分绕了k个半圈的纸带（Mk）。不过本文只探究2等分的情况，感兴趣的读者可以自行探究更一般的情况。

　　实验发现：

　　若k=1，结果是1个M4；若k=2，结果是2个M2；

　　若k=3，结果是1个M8；若k=4，结果是2个M4；

　　若k=5，结果是1个M12；若k=6，结果是2个M6；

　　发现什么规律了吗？

　　我们发现：如果k是奇数，会得到1个M(2k+2)；如果k是偶数，会得到2个Mk。这一规律对任意的k是否都成立呢？

　　答案仍然是肯定的。假如我们把纸带以1/2为界涂成红、蓝两种颜色，当在扭了奇数个半圈之后，红色的端头会连接蓝色，蓝色的端头会连接红色，因此，结果只有1根纸带。那么，为什么k每增加2，扭转半圈数会增加4呢？可以这样理解：上下两半都多拧了2个半圈，叠加在一起，就是4个半圈。

　　反之，当在扭了偶数个半圈之后，红色的端头连接的依然是红色端头，如果这时候将纸带裁成两半，必然会得到红、蓝两根纸带，而且其各自的扭转圈数与总的扭转圈数相同。

　　三、2等分组合莫比乌斯带

　　前面我们都是等分一条纸带，如果等分的是组合在一起的两条莫比乌斯带（M1）或纸环（M0），结果又会怎么样呢？

　　1）如果我们分别把两个M0，M1与M0，两个M1平行放置，并把其中一小段粘连在一起（分别记作M0+M0、M0+M1、M1+M1），然后按照下图的方式沿着两条带子的中间剪一刀，结果会得到什么呢？

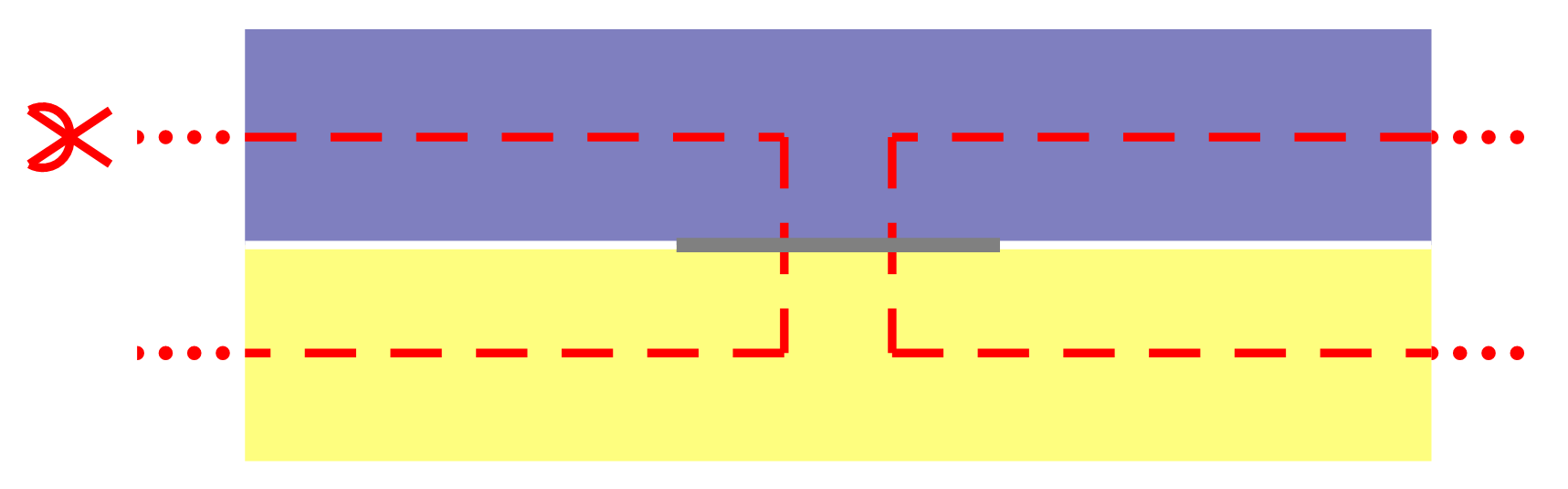
　　结果发现，第一种情况会得到M0+M0和M0；第二种情况会得到M0+M4；第三种情况，如果两个M1的扭转方向不同，会得到M0+M0；如果相同，会得到M2+M2，并且这两个M2是互相套在一起的。

　　上图是荷兰著名版画家埃舍尔的《骑士》，这一结构是将M2的上下两条边部分相连得到的。把其从中间一分为二，得到两个扭转方向相同的莫比乌斯带，因此这一结构其实就是M1+M1。

　　2）如果我们分别把两个M0，M1与M0，两个M1垂直粘连在一起（分别记作M0×M0、M0×M1、M1×M1），并从正中间剪开，结果会得到什么呢？

　　结果发现，前两者均得到一个正方形纸环（M0）。而第三者，如果两个M1的扭转方向相同，会得到两条船（M0）；如果不同，会得到两个套在一起的心形纸带（M2）。

　　关于莫比乌斯带，可以探究的问题还有很多，例如n等分Mk、n等分M(k1)+M(k2)、n等分M(k1)×M(k2)，还有纸带之间互相嵌套的情况等等。除此之外，笔者再提出一些问题供广大读者探究：这里的加法和乘法，它们是否满足交换律、结合律或分配律？这两种运算能描述什么样的曲面结构？能否对其做改进，使其能描述尽可能多的曲面结构？

　　最后提一下，如果将两个相同的莫比乌斯带的边完全粘合在一起，将会得到著名的克莱因瓶（实际上这样的操作无法在三维空间中实现，因此克莱因瓶只存在于四维及以上的空间中）。克莱因瓶是一个非常奇特的结构，因数学家F.克莱因最先发现而命名。它只有一个面，没有边。一只苍蝇可以从它的外部飞到它的内部，而无需穿过其边界。

　　拿起你手中的纸和剪刀，与这个有趣的带子来一番邂逅吧！

　　参考资料：

　　1.十万个为什么·数学卷，少年儿童出版社，p118-119