相关系数

　　相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标，是研究变量之间线性相关程度的量，一般用字母 r 表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊相关系数。

　　相关表和相关图可反映两个变量之间的相互关系及其相关方向，但无法确切地表明两个变量之间相关的程度。相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度；着重研究线性的单相关系数。

　　需要说明的是，皮尔逊相关系数并不是唯一的相关系数，但是最常见的相关系数，以下解释都是针对皮尔逊相关系数。

　　依据相关现象之间的不同特征，其统计指标的名称有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数（相关系数的平方称为判定系数）；将反映两变量间曲线相关关系的统计指标称为非线性相关系数、非线性判定系数；将反映多元线性相关关系的统计指标称为复相关系数、复判定系数等。

　　定义

　　相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。

　　简单相关系数：又叫相关系数或线性相关系数，一般用字母r 表示，用来度量两个变量间的线性关系。

　　定义式

　　其中，Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差

　　复相关系数：又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如，某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。

　　典型相关系数：是先对原来各组变量进行主成分分析，得到新的线性关系的综合指标，再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。

　　性质

　　这里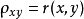， ， 是一个可以表征 和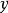 之间线性关系紧密程度的量。它具有两个性质：

　　（1）

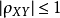
　　（2） 的充要条件是，存在常数a，b，使得

　　由性质衍生：

　　a. 相关系数定量地刻画了 X 和 Y的相关程度，即 越大，相关程度越大； 对应相关程度最低；

　　b. X 和Y 完全相关的含义是在概率为1的意义下存在线性关系，于是 是一个可以表征X 和Y 之间线性关系紧密程度的量。当 较大时，通常说X 和Y相关程度较好；当 较小时，通常说X 和Y相关程度较差；当X和Y不相关，通常认为X和Y之间不存在线性关系，但并不能排除X和Y之间可能存在其他关系。2

　　不相关和独立

　　若X和Y不相关， ，通常认为X和Y之间不存在线性关系，但并不能排除X和Y之间可能存在其他关系；若 ，则X和Y不相关。

　　若X和Y独立，则必有 ，因而X和Y不相关；若X和Y不相关，则仅仅是不存在线性关系，可能存在其他关系，如 ，X和Y不独立。

　　因此，“不相关”是一个比“独立”要弱的概念。2

　　生活示例

　　软件公司在全国有许多代理商，为研究它的财务软件产品的广告投入与销售额的关系，统计人员随机选择10家代理商进行观察，搜集到年广告投入费和月平均销售额的数据，并编制成相关表，见表1:

　　表1　广告费与月平均销售额相关表　单位：万元

　　参照表1，可计算相关系数如表2：

　　相关系数为0.9942，说明广告投入费与月平均销售额之间有高度的线性正相关关系。

　　应用概率论

　　【例】若将一枚硬币抛n次，X表示n次试验中出现正面的次数，Y表示n次试验中出现反面的次数。计算ρXY。

　　解：由于X+Y=n，则Y=-X+n，根据相关系数的性质推论，得ρXY = − 1。

　　企业物流

　　【例】一种新产品上市。在上市之前，公司的物流部需把新产品合理分配到全国的10个仓库，新品上市一个月后，要评估实际分配方案与之前考虑的其他分配方案中，是实际分配方案好还是其中尚未使用的分配方案更好，通过这样的评估，可以在下一次的新产品上市使用更准确的产品分配方案，以避免由于分配而产生的积压和断货。表1是根据实际数据所列的数表。

　　通过计算，很容易得出这3个分配方案中，B的相关系数是最大的，这样就评估到B的分配方案比实际分配方案A更好，在下一次的新产品上市分配计划中，就可以考虑用B这种分配方法来计算实际分配方案。

　　聚类分析

　　【例】如果有若干个样品，每个样品有n个特征，则相关系数可以表示两个样品间的相似程度。借此，可以对样品的亲疏远近进行距离聚类。例如9个小麦品种(分别用A1,A2,...,A9表示)的6个性状资料见表2，作相关系数计算并检验。

　　由相关系数计算公式可计算出6个性状间的相关系数，分析及检验结果见表3。由表3可以看出，冬季分蘖与每穗粒数之间呈现负相关(ρ = − 0.8982)，即麦冬季分蘖越多，那么每穗的小麦粒数越少，其他性状之间的关系不显著。

　　缺点

　　需要指出的是，相关系数有一个明显的缺点，即它接近于1的程度与数据组数n相关，这容易给人一种假象。因为，当n较小时，相关系数的波动较大，对有些样本相关系数的绝对值易接近于1；当n较大时，相关系数的绝对值容易偏小。特别是当n=2时，相关系数的绝对值总为1。因此在样本容量n较小时，我们仅凭相关系数较大就判定变量x与y之间有密切的线性关系是不妥当的。

　　本词条内容贡献者为:

　　胡启洲 - 副教授 - 南京理工大学