“光”跑的这么快，它的速度是如何测量的？

　　出品：科普中国

　　制作：陈星

　　监制：中国科学院计算机网络信息中心　 

　　想必大家在日常生活中都有这样的经验，在雷雨天气，我们总是先看到闪电的光，然后过了好久才听到轰隆隆的雷声。这其中的原因也不难理解，那就是因为光的速度比声音的速度快多了。

　　闪电（图片来自https://steemkr.com/cryptocurrency/@ontheverge/successful-lighting-test-is-it-a-bitcoin-savior）

　　空气中声音的速度大概是340m/s，一马赫的速度，就是指的是声音在空气中的速度。对于光，它的速度似乎是无限的，在日常生活中，光似乎能瞬间从一个地点到另一个地点，例如我们打开手电筒，几乎就在同时我们就看到了手电筒发出的光传播的很远。其实光的速度也是有限的，只不过非常大。

　　光在空气中的速度约为3*10^⁸ m/s。这个速度有多快呢？光在一秒钟内前进的距离大约就可以绕地球赤道7圈半，也就是说，几乎一眨眼的时间光就可以毫不费力的环游世界。从地球到月球的距离约为38万公里，光打个来回也仅仅需要两秒多（事实上，地球和月球之间的准确距离就是计算激光来回所花费时间得到的）。而人类在1969年第一次登上月球，花费了三天多的时间才到达月球，由此可见光速有多快。光速是目前人类已知速度的上限，没有什么东西能运动的比光速还快。既然光速这么快，那科学家们是如何知道光速的准确数值的呢？

　　激光测距（图片来自https://www.flickr.com/photos/gsfc/3951835665）　　 

　　光速测量史

　　人类历史上首次测量光速是在1676年。当时丹麦天文学家奥勒·罗默通过研究木星的卫星木卫一发现光速是有限的，并不是无限的，并由此估计出了光速的值。他估算的过程如下图所示：

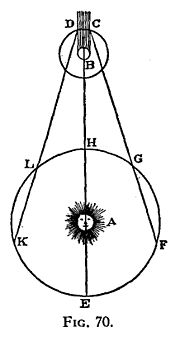
　　光速的估量（图片来自（https://en.wikipedia.org/wiki/Speed_of_light））

　　其中的大环是地球绕太阳的轨道，小环是木卫一绕木星的轨道。当地球远离木星（从L到K）和接近木星（从F到G）时，木卫一从木星的阴影里（C到D）出来的时间会产生变化，从这个变化可以就知道光速是有限的，再加上木卫一绕木星的公转周期和地球的公转周期以及公转速度，就可以估算出光速了。从这中方法估计出的光速误差很大，约为2.2x10^⁸m/s, 比实际值小26%。

　　在1728年，英国天文学家詹姆斯·布拉德利进一步提高了光速的准确度。他所使用的是恒星的光行差。光行差如下图所示

　　光行差示意图（图片来自https://en.wikipedia.org/wiki/Aberration_of_light）　　 

　　光行差，简单的来说就是地球的运动，会使恒星的方位产生变化。举例来说就是，假设在无风的天气里下雨，雨滴会垂直下落到你的身上，当你以一定的速度奔跑是，雨滴就会以另外一个角度落到你身上，不再垂直。结合这个角度的改变和你的速度，就可以估计出雨滴下落的速度。同样使用恒星光行差，结合地球的公转速度和恒星角度的变化，就可以估算出光速。使用这种方法估算出的光速约为3.01*10^⁸ m/s，误差仅仅为0.4%。　　 

　　新思路：如何提升光速测量精度？

　　首次准确在地球上，而不是依靠天体运动来测量光速的实验是在1849年由法国物理学家阿曼德·斐索实行的，他使用的方法叫做齿轮测速法。

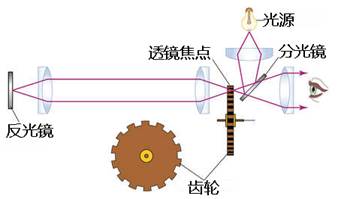
　　齿轮法测光速（图片来自https://www.illustrationsource.com/stock/image/506779/in-1849-french-physicist-armand-fizeau-used-this-method-to-achieve-the-first-terrestrial-measurement-of-the-speed-of-light/）　　 

　　这个方法的关键在于齿轮的转速，齿轮从很低的转速开始逐渐提速，在转速提升到某一关键速度的时候，齿轮转过两个齿的角度时，光线刚好从远处的镜子里折回。这样根据两齿之间的角度以及齿轮的转速，镜子的距离就可以计算出光速的大小。假设齿轮的转速刚好是 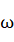，齿轮一共有N个齿，远处的镜子距离观察者L。那么光速=L*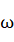*N/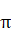

　　1849年阿曼德·斐索用这种装置测出的光速是3.15*10^⁸m/s，误差为5%，但是随后，法国科学家莱昂·傅科（就是用傅科摆演示地球自转的那个科学家），提高了这个装置的精确度，用旋转镜面代替了旋转的之轮，测出了2.98*10^⁸m/s的光速值，误差缩小到了0.5%. 旋转齿轮法和旋转镜面法对于光速的准确测量产生了很深远的影响，这种方法简单易行，结果很有说服力。直到1926年，这种方法都一直被当做测量光速的首选,精度一直提高到了0.001%左右。

　　齿轮测速法较为精确并且可信地测出了光速的值。之后不久（1861-1862年）就出现了伟大的麦克斯韦（1831-1879，苏格兰物理学家），给出了麦克斯韦方程组，完美的描述了电磁波的运动，他从方程组中得出电磁波的速度约为c=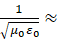3*10^⁸m/s，非常接近当时光速的值，于是他大胆的猜测光就是一种特殊频率的电磁波。后来的实验确实证明了他的猜测。

　　史上最伟大的物理学家之一—詹姆斯·克拉克·麦克斯韦（图片来自：维基百科）

　　当知道光是电磁波之后，我们就可以从另外一种方式得到准确的光速，那就是通过测量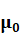（真空磁导率）和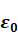（真空介电常数）来计算光速，也就是上面提到的c=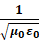。在1907年，美国科学家爱德华（Edward Bennett Rosa）和多尔西（N.E. Dorsey）通过这种方法给出了当时最精确的光速值2.99788*10^⁸m/s，误差仅仅为0.003%.。

　　20世纪50年代以后，随着电子工业技术的发展，各种测量光速的新技术相继出现，例如谐振腔法（1950年），无线电干涉法（1958年），激光干涉法（1972年）等。下面我们一一介绍。

　　谐振腔法主要依据的物理原理就是光也是电磁波，因为任意波长的电磁波具有相同的速度，而电磁波的速度和它的波长和频率之间存在如下的关系：速度=波长*频率。谐振腔法通过腔的尺寸可以很准确计算出里面电磁波的波长，而电磁波的频率又是已知的，因此，可以直接用上述公式计算出光的速度（或者说电磁波的速度）。

　　最后一种要说的就是激光干涉法了。目前各种资料查到的光速的值 299792458m/s，是通过激光干涉法测量出来的。无线电干涉和激光干涉本质上是一样的，因为它们都使用的是电磁波，只是波长不相同而已。因此我们只介绍激光干涉法。

　　想象一下水波，如下图所示，当两个水波相遇时，会产生干涉。当波峰和波峰（或波谷和波谷）相遇时，产生相加干涉，当波峰和波谷相遇时，会产生相消干涉。同样的道理对于光或者激光也是成立的。

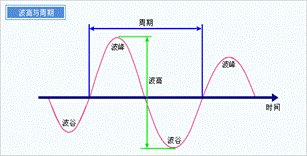
　　水波干涉和波峰波谷示意图（图片1来自https://www.ligo.caltech.edu/page/what-is-interferometer图片2来自http://gk-web.hkd.mlit.go.jp/hkop-bousai/fChn/puYougo.html）

　　激光干涉条纹（图片来自https://www.slideshare.net/hassang66/calibration-of-coordinate-measuring-machines-cmm）

　　激光是一种高度相干的光，因此很适合用于进行干涉。从激光器发出的光的频率是已知的，精度可以达到10^^-9赫兹 左右，波长的测量是通过法布里-珀罗干涉仪测量并和基准波长86-氪605nm的光谱线进行比较得到的，精度也可以达到10^^-9m左右。由于激光干涉对于波长的要求非常的高，产生的干涉条纹和激光的波长密切相关，因此通过干涉条纹可以十分准确的计算出激光的波长。有了激光的频率和波长，就可以计算出光速了：光速=频率*波长。

　　1972年通过激光干涉法测出的光速值是299792.4562±0.0011m/s, 这时当时能达到的最高的精度了，因为当时米的定义是通过86-氪605nm的光谱线给出的，它的精度限制了光速精度的进一步提高。

　　不久后的1983年，国际计量大会直接规定光速的值为299792458m/s, 并且反过来用光速重新定义了米。也就是说现在的光速值是给定的，不会再改变了，精度也不会再继续提高了，因为它已经成了“米”这个基本单位的基准。所谓的基准，就是指“米”这个单位的最高精度是由光速的值给出的，因为光速值具有很好的稳定性和重复性。

　　从光速测量的历史可以看出，科学的进步并不是一蹴而就的，有时候需要好几代科学家的不懈努力才能实现。光速测量精度的不断提高，到现在成了一个确定的值，这对于物理学的发展来说十分重要。因为光速是物理中一个重要的常数，著名的质能方程 E=mc^²， 狭义相对论中的“尺缩钟慢”效应，广义相对论中的引力波，时空弯曲等等，都和光速密切相关。

　　（本文中标明来源的图片均已获得授权）