出品:科普中国
制作:中科院物理所科学传播协会
监制:中国科学院计算机网络信息中心
19世纪中后期,麦克斯韦等人建立起了一套相当完备的经典电磁学理论体系,这个体系几乎可以解释当时所有的电磁现象。在这套体系中,有一个很特殊的量——磁矢势,通过对磁矢势求旋度,我们可以得到磁感应强度。

麦克斯韦所著的《电磁通论》,经典电磁理论的旷世之作
(图片来源:书籍封面)
然而,磁矢势与磁感应强度并不是一一对应的,如果将矢势后面加上一个额外全导数项,我们还是能得到相同磁感应强度,而这种变换也叫做规范变换。也就是说,磁矢势是规范变化的(因此也成为规范势),而磁感应强度是规范不变的。
一直以来,我们都相信物理世界不能依赖于我们怎么选取规范。因此,在这样的意义下,人们一度认为磁矢势并不是物理的。因为它不能被直接观测到,只是提供了数学上的计算便利,反映不了任何物理。这个认识在人们心中一直持续了将近一个世纪,直到1959年,阿哈罗诺夫-玻姆效应横空出世,人们的这个观念才开始动摇。
阿哈罗诺夫-玻姆效应
1959年,阿哈罗诺夫与玻姆二人合作在《物理评论》中发表了一篇文章。文中,他们提出了一个关于电子在磁场中运动的干涉假想实验(如下图所示):两束电子同时从A点出发,分别经过B,C再同时到达F点,并且在ABFC中间放置一个螺线管,他们从理论计算中发现这两束电子最终到达F点时会差一个固定的相位,这个相位差只依赖与螺线管里的磁通,不依赖与空间规范势的选取,也就是说它是规范不变的。
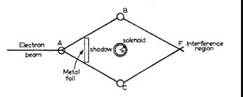
AB效应原理图
(图片来源:参考文献[3])
我们仔细分析不难发现,对于这样一个体系,磁场仅仅存在于螺线管里面,整个路径ABFC中,电子都是感受不到磁场的,既然感受不到磁场,两种路径又是完全对称的,那么这个相位差是从哪里来的呢?
阿哈罗诺夫与玻姆给出的解释是:在电磁场中,磁感应强度并没有包含所有的信息,其规范势才是更本质的。因为,虽然两束电子在运动过程中都感受不到磁感应强度,但是其运动过程中感受到的矢势一直不一样,从而累计了相位差。因此,这个思想实验阐明了规范势本身就可以直接产生可观测效应,并不只是个数学把戏,他能实实在在地反映物理。
很快,第二年,阿哈罗诺夫与玻姆的理论就被钱伯斯(Chambers)的实验所证实。后来,该现象也被学界称之为阿哈罗诺夫-玻姆效应,简称AB效应。值得一提的是,A和B既是两位发现者的名字首字母,也分别是磁矢势与磁感应强度的字母标记,因此,这也赋予了AB效应的另一个更加深刻的涵义。

亚基尔· 阿哈罗诺夫
(图片来源:维基百科)

戴维·玻姆
(图片来源:维基百科)
注:规范势只是可以产生可观测效应,但本身还是一个不可观测量,因为只有规范不变的物理量才能是可观测量。AB效应中,由规范势直接产生的这个相位差才是规范不变的,是个可观测量。
贝里相位
1984年,贝里在研究中发现,当一个系统的哈密顿量依赖于一个随时间周期变化的参量时,在绝热近似条件下,系统的在演化一个时间周期后,除了会累积一个固有的动力学相位以外,还会多出一个特殊的相位。

迈克尔·贝里
(图片来源:维基百科)
贝里仔细研究这个特殊的相位后发现,这个相位其实并不依赖于绝热条件,他是个系统内禀的属性,同时也不依赖参数的变化路径,只依赖于其初始与最终的取值。因此,贝里把这个特殊的相位称作是几何相位,后人也将其称为贝里相位。
通过前文,我们发现AB效应与贝里相位似乎除了都与相位有关外没有其他任何联系。其实不然,他们都具有同一种数学结构。我们完全可以认为AB效应是贝里相位的一个具体的物理实现,贝里相位是广义的AB效应。
几何相位与拓扑
AB效应与贝里相位除了阐明了规范势才是更为本质的,且能产生直接的可观测效应以外。其另一个重要价值在于,帮助我们更加深刻地理解了物理学中的拓扑效应。前面我们已经提过,贝里相位并不依赖于参数变化的路径,这种特性事实上就是我们经常所说的拓扑,即在连续形变下保持不变。
例如现在凝聚态物理学中非常火热的拓扑绝缘体与拓扑超导体,都与贝里相位息息相关。我们知道,在拓扑绝缘体中,陈数是一个非常重要物理量,因为它能表征两种不同的物态是否拓扑等价,而事实上,这个陈数的2π倍就是动量空间中的贝里相位。再比如,近年来大家非常关注的固体系统中的马约拉纳费米子,这种准粒子的激发与AB效应也是分不开的。

2016年诺贝尔物理学奖颁给大卫·索利斯、邓肯·霍尔丹和迈克尔·科斯特利兹,奖励他们在理论上发现了物质的拓扑相变与拓扑相(图片来源:诺贝尔奖官网)
写在最后
总而言之,AB效应与贝里相位的发现对量子力学基本理论的完善有着不可替代作用,同时也加深了我们对拓扑物态的理解与认识。
参考文献
[1] 维基百科,Aharonov–Bohm effect,https://en.wikipedia.org/wiki/Aharonov-Bohm_effect
[2] 维基百科,Geometric phase,https://en.wikipedia.org/wiki/Geometric_phase
[3] Aharonov, Y; Bohm, D (1959). "Significance of electromagnetic potentials in quantum theory". Physical Review. 115 (3): 485–491.
[4] M. V. Berry (1984). "Quantal Phase Factors Accompanying Adiabatic Changes". Proceedings of the Royal Society A. 392 (1802): 45–57.

 科普中国APP
科普中国APP
 科普中国微信
科普中国微信
 科普中国微博
科普中国微博




















