[科普中国]-分牛问题与最小公倍数

老农夫临终前将三个儿子叫到自己的床前，立下了一份遗嘱。老农夫有17头牛，他说三个儿子可以分掉他的这17头牛，但是又规定了他们各自能拿到的占比：大儿子最勤劳，可以得到总数的1/2，二儿子能够分得总数的1/3，而小儿子只能分到总数的1/9。

于是，等到老农夫去世之后，三名兄弟就坐在一起讨论应当如何分牛。一开始的时候他们认为把牛分一下，又知道如何分，事情应当很简单才对。但是后来经过计算，无论怎么分也无法完美地将17头牛按照老农夫的说法分开。三兄弟将17分别乘以三个占比，发现，大儿子应当分得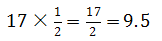头牛，二儿子应当分得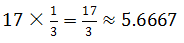头牛，小儿子应当分得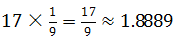头牛。这三个数字都不是整数，如果舍掉小数点后的部分，大儿子能分到9头牛，二儿子能分到5头牛，小儿子仅能分得1头牛，这样加起来仅有15头牛，需要杀死两头牛。再加上这样的分配方式也并不公平，因为，还会余下一头牛的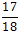。在这种情况下应该如何做呢？三兄弟十分焦急，难道这样就没有办法分得遗产，进而分家了吗？

他们找到了聪明博学的邻居，邻居提议借他们一头牛，分完再将这头牛还给他就好。

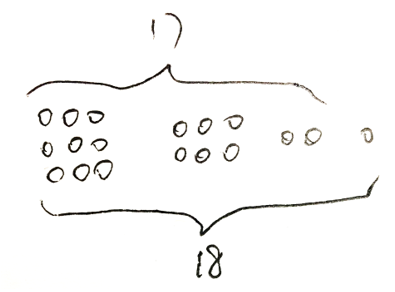
于是三兄弟依旧按照父亲所说的占比那样分牛，大儿子分得了18×1/2=9头牛，二儿子分得了18×1/3=6头牛，小儿子分得了18×1/9=2头牛，9+6+2=17，刚好分完了老农夫留下的17头牛，余下一头牛可以还给邻居。问题就这样解决了，三兄弟开开心心地回家了

邻居知道，老农夫提出1/2、1/3和1/9的说法，是想让他的三个儿子按照比例分配这17头牛，而化为整数之后刚好为9:6:2，所以按照9:6:2这样的比例去分配老农夫留下的17头牛就刚好能分完。

那么，为什么邻居需要借给三兄弟一头牛用来分遗产，还能将自己的这头牛拿回去呢？因为想要将1/2、1/3和1/9这三个数化为整数的比例，需要乘以这三个分数的公倍数18，再加上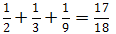，也就是说老农夫所提出的分配方式实际上是在分配18头牛中的17头，因此，邻居直接借出一头牛便可以免去自己向三兄弟解释一番的烦恼。

这里体现出的将分数比例转化为整数比例实际上应用了分母的最小公倍数的知识。公倍数指的是两个或多个整数公有的倍数，这样的数字有无数多个；其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。

最小公倍数通常可以用于分式化简为整式。有分数系数因式的等式，同时乘以这些分数系数的最小公倍数，就能将分数系数的等式或不等式化简为整数系数，以便对等式或不等式进一步计算。

本作品为“科普中国-科学原理一点通”原创，转载时务请注明出处。