[科普中国]-图像熵

图像熵（image entropy）是图像“繁忙”程度的估计值。

定义图像熵表示为图像灰度级集合的比特平均数，单位比特/像素，也描述了图像信源的平均信息量。对于离散形式的二维图像，其信息熵的计算公式为：1

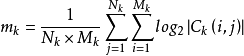
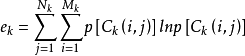
对于上式，其中，pi 为每一灰度级出现的概率。

熵指的是体系的混乱的程度，对焦良好的图像的熵大于没有清晰对焦的图像，因此可以用熵作为一种对焦评价标准。熵越大，图像越清晰。

图像的熵是一种特征的统计形式，它反映了图像中平均信息量的多少，表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。

熵的特性可以用很少的标准来描述熵的特性，将在下面列出。任何满足这些假设的熵的定义均正比以下形式

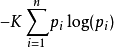
其中，K是与选择的度量单位相对应的一个正比常数。

下文中，pi= Pr(X=xi)且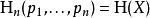

连续性该量度应连续，概率值小幅变化只能引起熵的微小变化。

对称性符号xi重新排序后，该量度应不变。

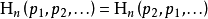
极值性当所有符号有同等机会出现的情况下，熵达到最大值（所有可能的事件同等概率时不确定性最高）。

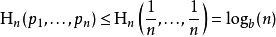
等概率事件的熵应随符号的数量增加。

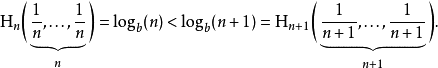
可加性熵的量与该过程如何被划分无关。

最后给出的这个函数关系刻画了一个系统与其子系统的熵的关系。如果子系统之间的相互作用是已知的，则可以通过子系统的熵来计算一个系统的熵。

给定n个均匀分布元素的集合，分为k个箱（子系统），每个里面有b1, ...,bk个元素，合起来的熵应等于系统的熵与各个箱子的熵的和，每个箱子的权重为在该箱中的概率。

对于正整数bi其中b1+ ... +bk=n来说，

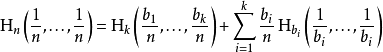
选取k=n，b1= ... =bn= 1，这意味着确定符号的熵为零：Η1(1) = 0。这就是说可以用n进制熵来定义n个符号的信源符号集的效率。参见信息冗余。

进一步性质熵满足以下性质，借由将熵看成“在揭示随机变量X的值后，从中得到的信息量（或消除的不确定性量）”，可来帮助理解其中一些性质。

增减一概率为零的事件不改变熵：

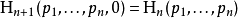
可用琴生不等式证明

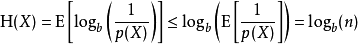
具有均匀概率分布的信源符号集可以有效地达到最大熵logb(n)：所有可能的事件是等概率的时候，不确定性最大。

计算 (X,Y)得到的熵或信息量（即同时计算X和Y）等于通过进行两个连续实验得到的信息：先计算Y的值，然后在你知道Y的值条件下得出X的值。写作

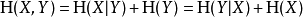
如果Y=f(X)，其中f是确定性的，那么Η(f(X)|X) = 0。应用前一公式Η(X,f(X))就会产生

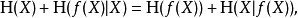
所以Η(f(X)) ≤ Η(X)，因此当后者是通过确定性函数传递时，变量的熵只能降低。

如果X和Y是两个独立实验，那么知道Y的值不影响我们对X值的认知（因为两者独立，所以互不影响）：

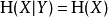
两个事件同时发生的熵不大于每个事件单独发生的熵的总和，且仅当两个事件是独立的情况下相等。更具体地说，如果X和Y是同一概率空间的两个随机变量，而(X,Y)表示它们的笛卡尔积，则

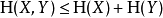在前两条熵的性质基础上，很容易用数学证明这一点。

信息熵在信息论中，熵（英语：entropy）是接收的每条消息中包含的信息的平均量，又被称为信息熵、信源熵、平均自信息量。这里，“消息”代表来自分布或数据流中的事件、样本或特征。（熵最好理解为不确定性的量度而不是确定性的量度，因为越随机的信源的熵越大。）来自信源的另一个特征是样本的概率分布。这里的想法是，比较不可能发生的事情，当它发生了，会提供更多的信息。由于一些其他的原因，把信息（熵）定义为概率分布的对数的相反数是有道理的。事件的概率分布和每个事件的信息量构成了一个随机变量，这个随机变量的均值（即期望）就是这个分布产生的信息量的平均值（即熵）。熵的单位通常为比特，但也用Sh、nat、Hart计量，取决于定义用到对数的底。

采用概率分布的对数作为信息的量度的原因是其可加性。例如，投掷一次硬币提供了1 Sh的信息，而掷m次就为m位。更一般地，你需要用log2(n)位来表示一个可以取n个值的变量。

在1948年，克劳德·艾尔伍德·香农将热力学的熵，引入到信息论，因此它又被称为香农熵。

对比信息熵的意义：信源的信息熵H是从整个信息源的统计特性来考虑的。它是从评价意义上来表征信息源的总体特征的。对于某特定的信息源，其信息熵只有一个。不同的信息源因统计特性不同，其熵也不同。

图像的信息熵的意义：它表征图像灰度分布的聚集特性，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。

参见熵 (生态学)

熵 (热力学)

熵编码

麦克斯韦妖

本词条内容贡献者为:

曹慧慧 - 副教授 - 中国矿业大学