[科普中国]-线性二次型最优控制

使用二次型性能指标的线性系统最优控制。

定义使用二次型性能指标的线性系统最优控制。它可得到状态线性反馈的最优控制规律，便于实现闭环最优控制，是应用广泛的最优控制方式。

性能指标线性系统状态方程及输出方程为

x(t)=A(t)x(t)+B(t)u(t) (1)

y(t)=C(t)x(t) (2)

式中x(t)为n维状态向量;u(t)为p维控制向量;y(t)为q维输出向量。设z(t)为理想输出向量，与y(t)同维数，并定义

e(t)=z(t)-y(t) (3)

误差向量。线性二次型最优控制问题的性能指标为

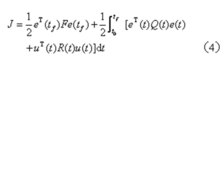
这里，权函数F、Q(t)为正半定矩阵，R(t)为正定矩阵。假设tf固定。要求寻找最优控制u*(t)，使性能指标J为最小。被积函数的第一项表明误差e(t)的大小，是非负的。其第二项表明控制功率的大小，对应于u≠0它恒为正。因此，对u(t)往往不需再加约束，而常设u(t)为自由的。性能指标的第一项则表示终值误差。

状态调节器问题系统状态方程如式 (1)所示，u(t)不受约束，tf固定，性能指标为

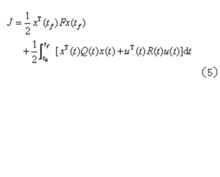
寻找最优控制u*(t)，使性能指标J为最小。

用极小值原理或动态规划法，可得下列矩阵黎卡提微分方程(一阶非线性微分方程)

P(t)=-P(t)A(t)-AT(t)P(t)+P(t)B(t)R-1(t)BT(t)P(t)-Q(t) (6)

其边界条件为

P(tf)=F (7)

由式(6)解出P(t)后，可得最优控制规律为

u*(t)=-R-1(t)BT(t)P(t)x*(t) (8)

由式(8)可以看出，最优控制规律是一个状态线性反馈规律，控制向量u*(t)由状态向量x*(t)生成，构成状态反馈，并且呈线性关系。这样，能方便地实现闭环最优控制，这一点在工程上具有十分重要的意义。

P(t)是一对称矩阵，一般都要由计算机求出方程(6)的数值解。P(t)是时间函数，即使线性系统是定常的，为了实现最优控制，反馈增益应该是时变的，而不是常值反馈增益。这一点与经典控制方法的结论有本质的差别。1

可以求得性能指标的最小值为

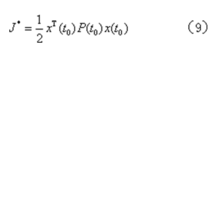
tf=∞时的状态调节器问题 定常系统方程为

x(t)=Ax(t)+Bu(t) (10)

这里，A、B为常值矩阵，u(t)不受约束，性能指标为

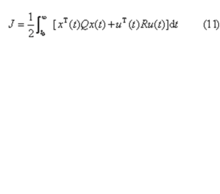
Q、R为常值矩阵，Q为正半定的，R为正定的。求最优控制u*(t)，使性能指标J为最小。

对于这样的系统，有(t)=0情况下的矩阵黎卡提方程

上式是矩阵黎卡提代数方程，它是非线性方程。求解该方程，可得最优控制为

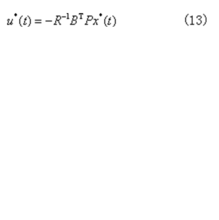
性能指标的最小值也由式(9)求得。

输出调节器问题 系统动态方程为式(1)、(2)，u(t)不受约束，tf固定，性能指标为

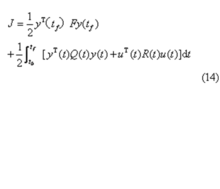
式中F和Q(t)为正半定矩阵;R(t)为正定矩阵。求最优控制u*(t)，使性能指标J为最小。

可将这类问题转化成等效的状态调节器问题，得：当且仅当系统完全可观测时，存在唯一的最优控制

其中，P(t)满足下列矩阵黎卡提方程

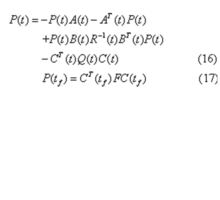
最优控制规律输出调节器的最优控制规律，并不是输出量y(t)的线性反馈，而仍是状态x(t)的线性反馈。仅由输出反馈时，没有充分利用全部信息，不能构成最优控制。2

完全可控、可观测的定常系统，tf=∞时的输出调节器问题，其最优控制存在并且是唯一的

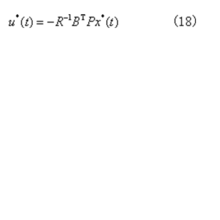
P为下列矩阵黎卡提代数方程的解

跟踪问题系统动态方程为式(1)、(2)，x(t0)=x0，系统完全可观测，理想输出为z(t)，误差向量为式(3)，性能指标为式(4)，u(t)不受约束，tf固定，求最优控制u*(t)，使性能指标J为最小。

用极小值原理来求解，并设

λ*(t)=P(t)x*(t)-g(t) (20)

可写出形如式(16)的黎卡提方程以及下式

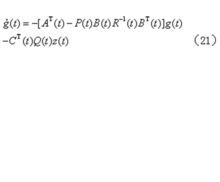
其边界条件为

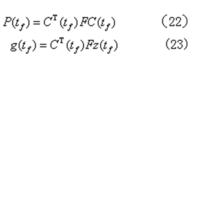
从而得最优控制规律

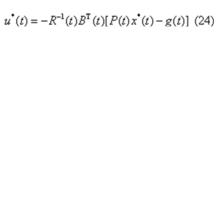
对于线性定常系统，当理想输出z(t)为常值、终端时刻tf极大但不为无穷大时，可以导出一个近似的最优控制规律如下，它具有很大的实用意义。

设系统状态方程如式(10)所示，x(t0)=x0，输出方程y(t)=Cx(t)，系统完全可控并完全可观测，理想输出z(t)=z0，tf足够大，性能指标为

则其最优控制存在并唯一，为

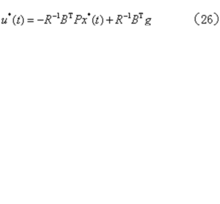
其中P和g依次满足下列两式

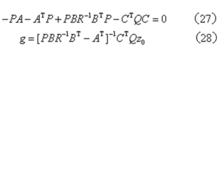
本词条内容贡献者为:

曹慧慧 - 副教授 - 中国矿业大学