[科普中国]-克列因-鲁特曼定理

克列因-鲁特曼定理是关于具有非负核的线性积分算子特征值与特征函数性质的一组结论。

简介克列因-鲁特曼定理是关于具有非负核的线性积分算子特征值与特征函数性质的一组结论。

设G是RN中的可测集，m(G)≠0，k(x,y):G×G→[0,+∞)，并且由k(x,y)所确定的线性积分算子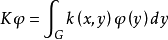映C(G)入C(G)是全连续算子。

主要内容1948年，克列因和鲁特曼利用锥理论和半序方法研究了线性积分算子正特征值和特征函数的性质，其主要内容有：

1、如果存在ψ∈C(G)\{φ∈C(G)|φ(x)≤0}，实数c>0以及正整数p，使得cKpψ≥ψ，则K具有对应于正特征函数的正特征值。

2、如果线性积分算子的谱半径r(K)≠0，则K必具有对应于r-1(K)的正特征函数。

3、如果K是u0有界算子，即存在u0∈{φ∈C(G)|φ(x)≥0}，u0≢0，使得对任给的φ∈{φ∈C(G)|φ(x)≥0}，都有正整数n及实数α>0，β>0，满足au0≤Knφ≤βu0，则K有且仅有一个就范特征函数。更进一步，K有且仅有一个对应于正特征函数的特征值，其代数重数为1。

应用克列因-鲁特曼定理对研究线性积分算子的性质有重要意义，它对于非线性积分方程和非线性微分方程的研究，也有很多应用。

目前，这一定理中的某些结论已经推广到非线性积分算子。1

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学